Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Với $x\in\mathbb{Z}^+$, để $N$ nguyên thì:
$\sqrt{x}-5$ là ước của $9$
$\Rightarrow \sqrt{x}-5\in \left\{\pm 1; \pm 2; \pm 3; \pm 9\right\}$
$\Rightarrow \sqrt{x}\in \left\{4; 6; 7; 3; 2; 8; 14; -4\right\}$
Do $\sqrt{x}\geq 0$ nên $\sqrt{x}\in \left\{4; 6; 7; 3; 2; 8; 14\right\}$
$\Rightarrow x\in \left\{16; 36; 49; 9; 4; 64; 196\right\}$

b/
Áp dụng BĐT Cô-si ta có:
$a^2(1+b^2)+b^2(1+c^2)+c^2(1+a^2)=a^2+b^2+c^2+a^2b^2+b^2c^2+c^2a^2$
$=(a^2+b^2c^2)+(b^2+c^2a^2)+(c^2+a^2b^2)$
$\geq 2\sqrt{a^2b^2c^2}+2\sqrt{b^2c^2a^2}+2\sqrt{c^2a^2b^2}$
$=2abc+2abc+2abc=6abc$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c=1$
c/
Áp dụng BĐT Cô-si:
$(a+b)(b+c)(c+a)\geq 2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ca}=8abc$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c$.

Lời giải:
Áp dụng BĐT Cô-si ta có:
$ab+\frac{a}{b}\geq 2a$
$ab+\frac{b}{a}\geq 2b$
$\frac{a}{b}+\frac{b}{a}\geq 2$
Cộng theo vế 3 BĐT trên ta thu được:
$2(ab+\frac{a}{b}+\frac{b}{a})\geq 2(a+b+1)$
$\Rightarrow ab+\frac{a}{b}+\frac{b}{a}\geq a+b+1$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=1$

1.
Áp dụng BĐT Cô-si:
$y=x+\frac{2}{x^2}=\frac{x}{2}+\frac{x}{2}+\frac{2}{x^2}\geq 3\sqrt[3]{\frac{x}{2}.\frac{x}{2}.\frac{2}{x^2}}=3\sqrt[3]{\frac{1}{2}}$
Vậy GTNN của $y$ là $3\sqrt[3]{\frac{1}{2}}$. Giá trị này đạt tại $\frac{x}{2}=\frac{2}{x^2}\Leftrightarrow x=\sqrt[3]{4}$
2.
\(y=(x+1)^2+(\frac{x^2}{x+1}+2)^2=(x+1)^2+(\frac{x^2+2x+2}{x+1})^2\\ =(x+1)^2+[\frac{(x+1)^2+1}{x+1}]^2=(x+1)^2+(x+1+\frac{1}{x+1})^2\)
Đặt $t=x+1$ thì, áp dụng BĐT Cô-si:
\(y=t^2+(t+\frac{1}{t})^2=2t^2+\frac{1}{t^2}+2\geq 2\sqrt{2t^2.\frac{1}{t^2}}+2=2\sqrt{2}+2\)
Vậy $y_{\min}=2\sqrt{2}+2$
Giá trị này đạt tại $2t^2=\frac{1}{t^2}\Leftrightarrow t=\pm \sqrt[4]{\frac{1}{2}}$
$\Leftrightarrow x=\pm \sqrt[4]{\frac{1}{2}}-1$

Lời giải:
Để $M=\frac{\sqrt{x}-1}{2}$ nguyên thì $\sqrt{x}-1$ là số nguyên lẻ.
Đặt $\sqrt{x}-1=2k+1$ với $k$ nguyên.
$\sqrt{x}=2k+2$
Có:
$2k+2=\sqrt{x}\geq 0\Rightarrow k\geq -1$
$2k+2=\sqrt{x}< \sqrt{50}< 8\Rightarrow k< 3$
Do $k$ là số nguyên nên $k\in\left\{-1; 0; 1; 2\right\}$
Khi đó:
$x\in \left\{0; 4; 16; 36\right\}$ (thỏa mãn)

\(A\left(x\right)⋮x-1\)
=>\(mx^2-mx+\left(m-n-1\right)x-m+n+1+m-n-1-3⋮x-1\)
=>m-n-4=0(2)
\(A\left(x\right)⋮x+1\)
=>\(mx^2+mx-\left(m+n+1\right)x-\left(m+n+1\right)+m+n-2⋮x+1\)
=>m+n-2=0(1)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}m+n=2\\m-n=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=6\\m+n=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=3\\n=2-3=-1\end{matrix}\right.\)
b: \(B\left(x\right)⋮x-2\)
=>\(\left(m+1\right)x^2-\left(2m+2\right)x+\left(2m+6\right)x-2\left(2m+2\right)+2\left(2m+2\right)+3⋮x-2\)
=>2(2m+2)+3=0
=>4m+7=0
=>\(m=-\dfrac{7}{4}\)
c: \(C\left(x\right)⋮x-1\)
=>\(\left(2n-3\right)x^2-\left(n+2\right)x-9⋮x-1\)
=>\(\left(2n-3\right)x^2-\left(2n-3\right)+\left(2n-3-n-2\right)x-9⋮x-1\)
=>\(\left(n-5\right)x-9⋮x-1\)
=>\(x\left(n-5\right)-\left(n-5\right)+n-5-9⋮x-1\)
=>n-14=0
=>n=14
d: \(D\left(x\right)⋮x-3\)
=>\(5x^2-15x+\left(-3n-1+15\right)x+7⋮x-3\)
=>\(\left(-3n+14\right)x+7⋮x-3\)
=>\(\left(-3n+14\right)x-3\left(-3n+14\right)+3\left(-3n+14\right)+7⋮x-3\)
=>3(-3n+14)+7=0
=>-9n+49=0
=>-9n=-49
=>\(n=\dfrac{49}{9}\)

\(x^3+x^2-x+a⋮x^2+2x+1\)
=>\(x^3+2x^2+x-x^2-2x-1+a+1⋮x^2+2x+1\)
=>a+1=0
=>a=-1

Hình bạn tự vẽ nhé, tại trên này chưa cho duyệt hình.
Ta thấy \(\widehat{BAQ}=\widehat{QCA}\) do chúng cùng phụ với \(\widehat{ABC}\)
Lại có \(\widehat{QAN}=\widehat{NAC}\) (do AN là phân giác của \(\widehat{QAC}\))
\(\Rightarrow\widehat{BAQ}+\widehat{QAN}=\widehat{QCA}+\widehat{NAC}\)
\(\Rightarrow\widehat{BAN}=\widehat{BNA}\) (vì \(\widehat{BNA}\) lá góc ngoài của tại N tam giác ACN)
\(\Rightarrow\Delta BAN\) cân tại B
Vì BK là đường cao của tam giác BAN cân tại B nên BK cũng là đường trung trực của tam giác BAN.
Lại có \(I\in BK\) nên \(IN=IA\).
Tương tự, ta cũng có \(IM=IA\) \(\Rightarrow IM=IN\left(=IA\right)\)
\(\Rightarrow\Delta IMN\) cân tại I (1)
Kéo dài tia AI và đặt là Ax. Khi đó \(\widehat{MIx}=\widehat{IAM}+\widehat{IMA}\) (do \(\widehat{MIx}\) là góc ngoài tại I của tam giác IAM) \(=2\widehat{MAx}\) (vì tam giác IAM cân tại I nên \(\widehat{IAM}=\widehat{IMA}\))
Tương tự, ta có \(\widehat{NIx}=2\widehat{NAx}\)
\(\Rightarrow\widehat{MIx}+\widehat{NIx}=2\left(\widehat{MAx}+\widehat{NAx}\right)\)
\(\Rightarrow\widehat{MIN}=2\widehat{MAN}\)
Mà \(\widehat{MAN}=\widehat{MAQ}+\widehat{NAQ}=\dfrac{1}{2}\left(\widehat{BAQ}+\widehat{CAQ}\right)=\dfrac{1}{2}\widehat{BAC}=45^o\)
Nên \(\widehat{MIN}=2.45^o=90^o\) (2)
Từ (1) và (2) \(\Rightarrow\Delta IMN\) vuông cân tại I (đpcm)

- 1,25 = \(\dfrac{-125}{100}\) = \(\dfrac{-125:25}{100:25}\) = \(\dfrac{-5}{4}\)
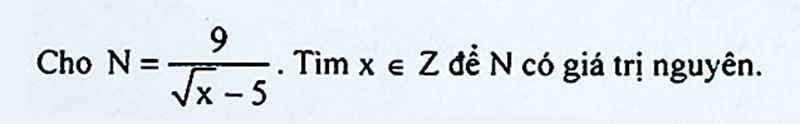
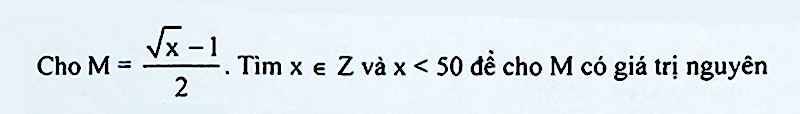

\(B=\left|x-2010\right|+\left|x-1963\right|\)
\(=\left|x-2010\right|+\left|1963-x\right|>=\left|x-2010+1963-x\right|\)
=>\(B>=\left|-47\right|=47\)
Dấu '=' xảy ra khi (x-2010)(x-1963)<=0
=>1963<=x<=2010