giải phương trình: 6x - 6 = 2x+ 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi vận tốc thực của ca nô khi nước lặng là \(x(km/h;x>0)\)
Vận tốc của ca nô khi đi xuôi dòng từ A đến B là: \(x+2(km/h)\)
Vận tốc của ca nô khi đi ngược dòng từ B về A là: \(x-2(km/h)\)
Vì ca nô đi từ A đến B hết 4 giờ rồi lại đi ngược dòng từ B về A hết 5 giờ nên ta có phương trình:
\(4\left(x+2\right)=5\left(x-2\right)\)
\(\Leftrightarrow4x+8=5x-10\)
\(\Leftrightarrow5x-4x=8+10\)
\(\Leftrightarrow x=18\) (tmđk)
Khi đó, độ dài quãng đường AB là: \(4\cdot\left(18+2\right)=80\left(km\right)\)
Gọi x (km) là khoảng cách giữa hai bến A và B, với x > 0.
Vì vận tốc xuôi dòng lớn hơn vận tốc ngược dòng chính bằng 2 lần vận tốc dòng nước nên ta có phương trình:
x = 80 (thỏa mãn điều kiện).
Vậy khoảng cách giữa hai bến A và B là 80km.

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: XétΔBAD vuông tại A và ΔBHE vuông tại H có
\(\widehat{ABD}=\widehat{HBE}\)
Do đó: ΔBAD~ΔBHE
=>\(\dfrac{BD}{BE}=\dfrac{AD}{HE}\)
=>\(\dfrac{BE}{BD}=\dfrac{EH}{AD}\)(1)
\(\widehat{ADE}+\widehat{ABD}=90^0\)(ΔABD vuông tại A)
\(\widehat{HEB}+\widehat{DBC}=90^0\)(ΔHBE vuông tại H)
mà \(\widehat{ABD}=\widehat{DBC}\)
nên \(\widehat{ADE}=\widehat{HEB}\)
=>\(\widehat{ADE}=\widehat{AED}\)
=>AD=AE(2)
Từ (1),(2) suy ra \(\dfrac{BE}{BD}=\dfrac{EH}{AD}=\dfrac{EH}{AE}\left(3\right)\)
Xét ΔBHA có BE là phân giác
nên \(\dfrac{EH}{AE}=\dfrac{BH}{BA}\left(4\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{DC}=\dfrac{BA}{BC}\left(5\right)\)
ΔABC~ΔHBA
=>\(\dfrac{BH}{BA}=\dfrac{BC}{BA}\left(6\right)\)
Từ (4),(5),(6) suy ra \(\dfrac{EH}{AE}=\dfrac{AD}{DC}\)
=>\(\dfrac{BE}{BD}=\dfrac{DA}{DC}\)

Bài 5:
a: Xét ΔAID vuông tại A và ΔDIK vuông tại D có
\(\widehat{AID}\) chung
Do đó: ΔAID~ΔDIK
=>\(\dfrac{IA}{ID}=\dfrac{ID}{IK}\)
=>\(ID^2=IA\cdot IK\)
b: Xét ΔADI vuông tại A và ΔAKD vuông tại A có
\(\widehat{ADI}=\widehat{AKD}\left(=90^0-\widehat{ADK}\right)\)
Do đó: ΔADI~ΔAKD
=>\(\dfrac{AD}{AK}=\dfrac{AI}{AD}\)
=>\(AD^2=AK\cdot AI\)
c: Xét ΔDEA vuông tại E và ΔDAI vuông tại A có
\(\widehat{EDA}\) chung
Do đó: ΔDEA~ΔDAI
=>\(\dfrac{DE}{DA}=\dfrac{DA}{DI}\)
=>\(DE\cdot DI=DA^2\left(1\right)\)
Xét ΔDFA vuông tại F và ΔDAK vuông tại A có
\(\widehat{FDA}\) chung
Do đó: ΔDFA~ΔDAK
=>\(\dfrac{DF}{DA}=\dfrac{DA}{DK}\)
=>\(DF\cdot DK=DA^2\left(2\right)\)
Từ (1),(2) suy ra \(DE\cdot DI=DF\cdot DK\)
d: DE*DI=DF*DK
=>\(\dfrac{DE}{DK}=\dfrac{DF}{DI}\)
Xét ΔDEF vuông tại D và ΔDKI vuông tại D có
\(\dfrac{DE}{DK}=\dfrac{DF}{DI}\)
DO đó: ΔDEF~ΔDKI

a) 6x - 6 = 2x + 10
6x - 2x = 10 + 6
4x = 16
x = 16 : 4
x = 4
Vậy S = {4}
b) Hệ số góc của đường thẳng y = 2x + 1 là 2
Do hệ số góc là 2 > 0 nên góc tạo bởi (d) và trục Ox là góc nhọn

| S(km) | V(km/h) | t(giờ) | |
| xe máy | 40.x | 40 | x |
| ô tô | 60.x | 60 | x |
đổi 20p = 1/5 giờ
pt:
40.x + 60.x = 120 - 120.1/5
Gọi thời gian kể từ ô tô xuất phát đến lúc hai xe gặp nhau là x(giờ)
(ĐK: x>0)
Sau 20p=1/3 giờ thì xe máy đi được: \(40\cdot\dfrac{1}{3}=\dfrac{40}{3}\left(km\right)\)
Độ dài quãng đường còn lại là:
\(120-\dfrac{40}{3}=\dfrac{320}{3}\left(km\right)\)
Do đó, ta có phương trình:
60x+40x=320/3
=>100x=320/3
=>\(x=\dfrac{320}{3}:100=\dfrac{320}{300}=\dfrac{16}{15}\left(nhận\right)\)
Vậy: Sau 16/15h kể từ ô tô xuất phát thì hai xe gặp nhau

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
=>\(AB^2=BH\cdot BC\)
b: xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC~ΔHAC
=>\(\dfrac{CA}{CH}=\dfrac{CB}{CA}\)
=>\(CA^2=CH\cdot CB\)
c: ΔABC~ΔHAC
ΔABC~ΔHBA
Do đó: ΔHAC~ΔHBA
=>\(\dfrac{HA}{HB}=\dfrac{HC}{HA}\)
=>\(HA^2=HB\cdot HC\)
d: \(\dfrac{1}{AH^2}=\dfrac{1}{HB\cdot HC}\)
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{BH\cdot BC}+\dfrac{1}{CH\cdot BC}\)
\(=\dfrac{1}{BC}\left(\dfrac{1}{BH}+\dfrac{1}{CH}\right)=\dfrac{1}{BC}\cdot\dfrac{BC}{BH\cdot CH}=\dfrac{1}{BH\cdot CH}\)
Do đó: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

a: Xét ΔBAD và ΔBCE có
\(\widehat{BAD}=\widehat{BCE}\left(=90^0-\widehat{HAC}\right)\)
Do đó: ΔBAD~ΔBCE
Xét ΔBHD vuông tại H và ΔBAE vuông tại A có
\(\widehat{HBD}=\widehat{ABE}\)
Do đó: ΔBHD~ΔBAE
c: ΔBAD~ΔBCE
=>\(\dfrac{AD}{CE}=\dfrac{BD}{BE}\left(1\right)\)
ΔBHD~ΔBAE
=>\(\dfrac{HD}{AE}=\dfrac{BD}{BE}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{AD}{CE}=\dfrac{HD}{AE}\)
=>\(\dfrac{AD}{DH}=\dfrac{CE}{AE}\)
=>\(\dfrac{HD}{DA}=\dfrac{EA}{EC}\)
c: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(\dfrac{BH}{3}=\dfrac{3}{5}\)
=>BH=9/5=1,8(cm)
BH+HC=BC
=>HC+1.8=5
=>HC=3,2(cm)

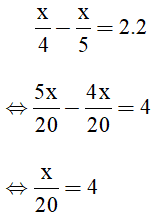
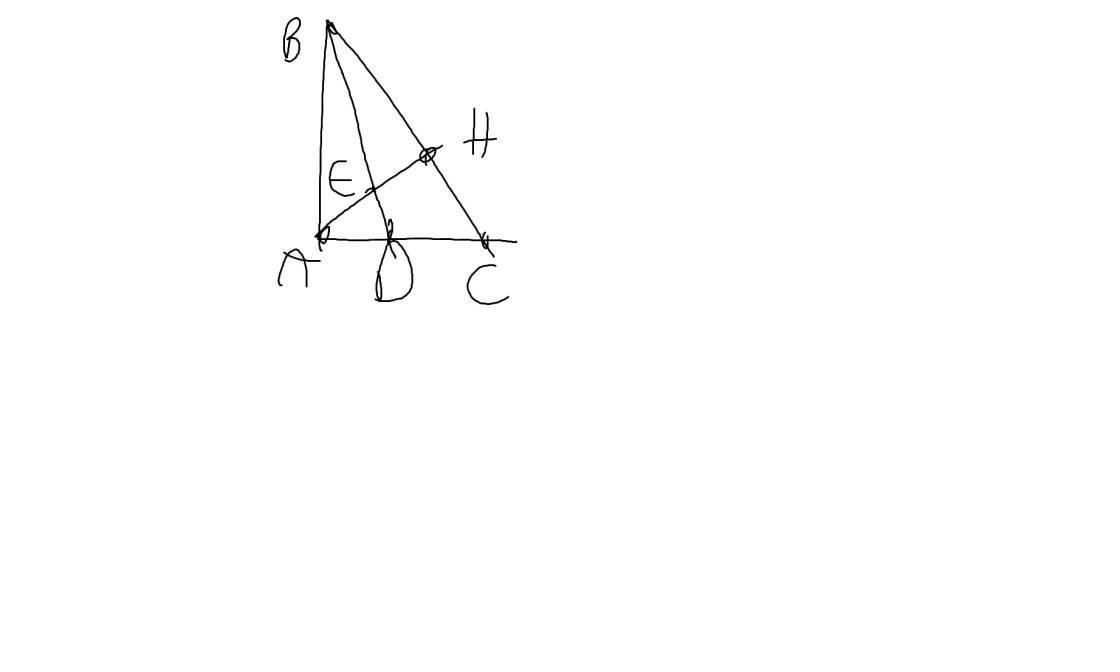


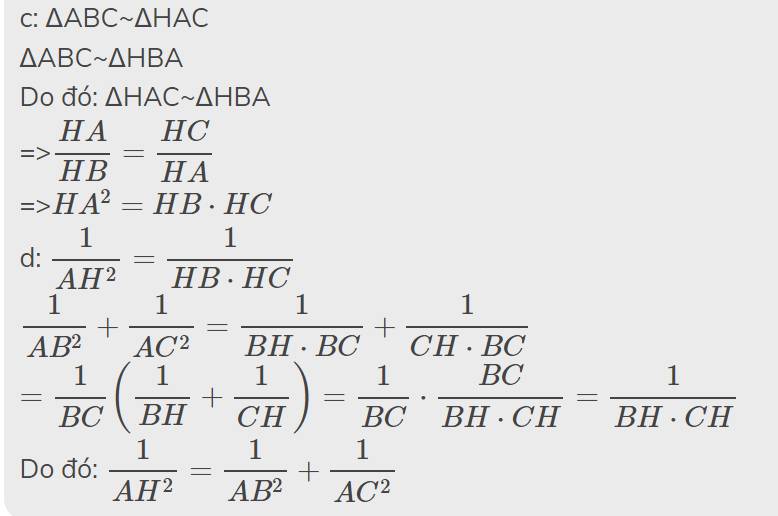

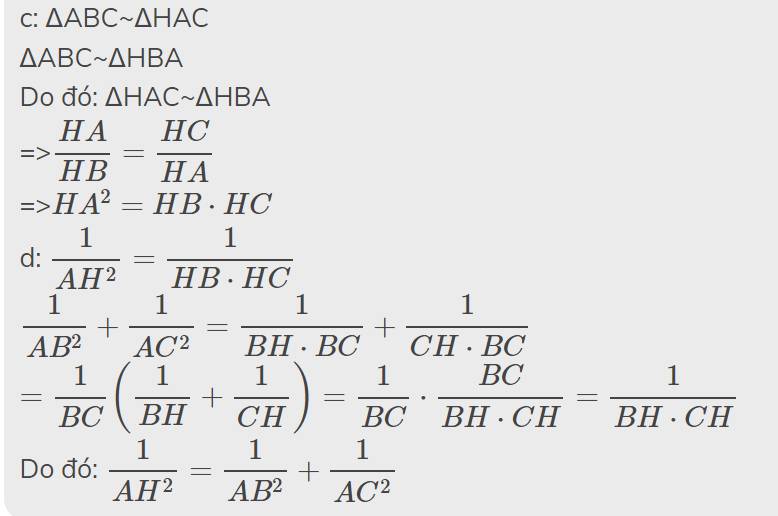
6x - 6 = 2x + 10
6x - 2x = 10 + 6
4x = 16
x = 16 : 4
x = 4
Vậy S = {4}