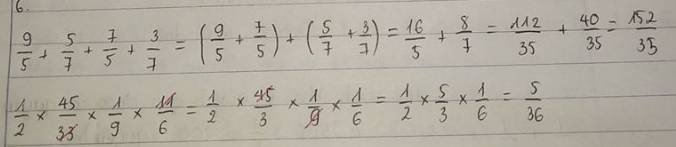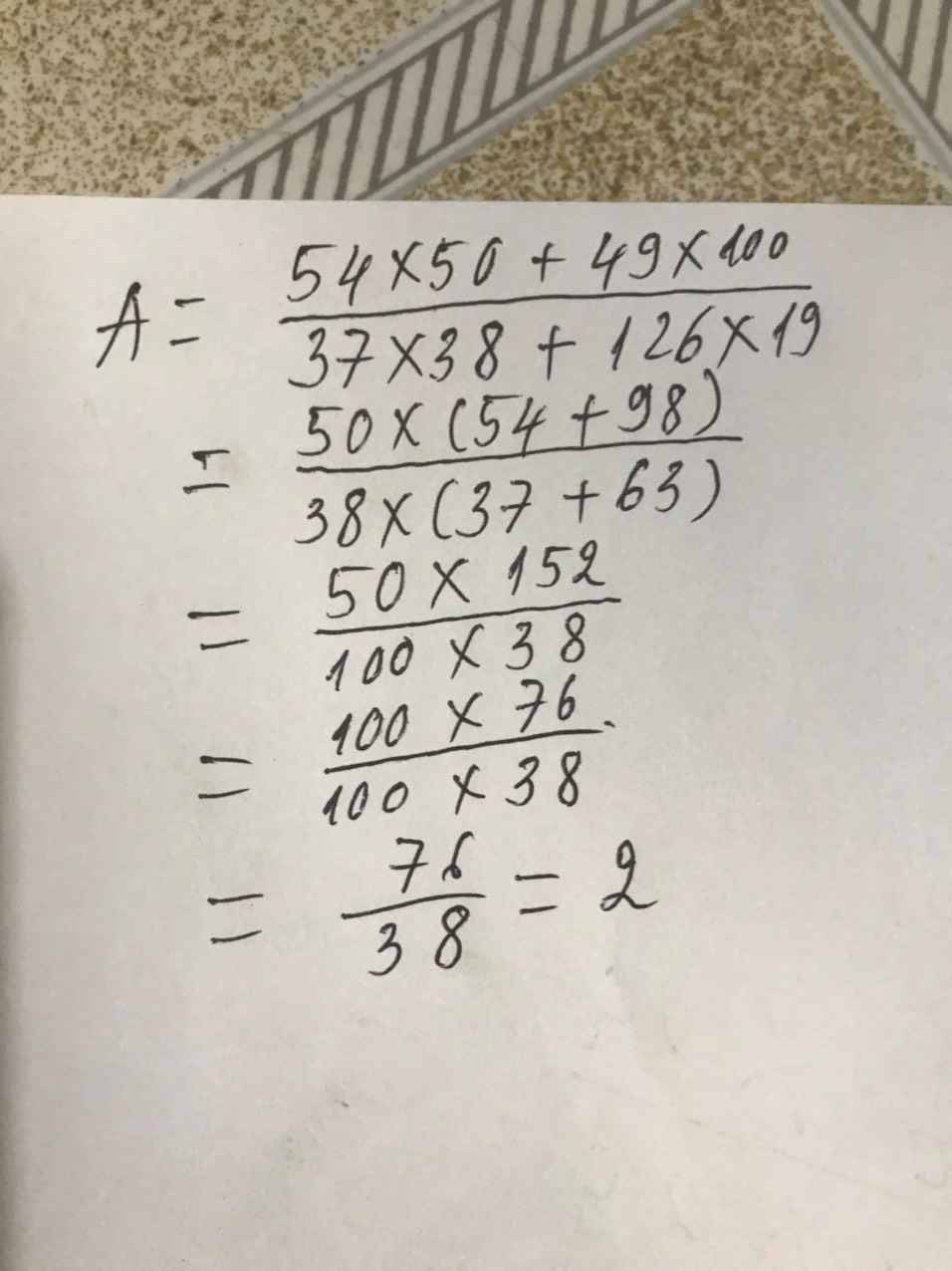A = 1 - \(\dfrac{1}{1.2}\) - \(\dfrac{1}{2.3}-\dfrac{1}{3.4}-\dfrac{1}{4.5}...-\dfrac{1}{97.98}\)

A= 1-\(\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{97.98}\right)\)

A= 1- \(\left(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}...+\dfrac{1}{97}-\dfrac{1}{98}\right)\)

A= 1- \(\left(\dfrac{1}{1}-\dfrac{1}{98}\right)\)

A=1-  1 + \(\dfrac{1}{98}\)

A= \(\dfrac{1}{98}\)

Lời giải:

$1-A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{97.98}$

$1-A=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{98-97}{97.98}$

$1-A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{97}-\frac{1}{98}$

$=1-\frac{1}{98}$

$\Rightarrow A=\frac{1}{98}$

\(\dfrac{6}{11}x=\dfrac{18}{5}z\) ⇒ \(\dfrac{18}{33}x=\dfrac{18}{5}z\) ⇒\(\dfrac{x}{33}=\dfrac{z}{5}\)

Áp dụng tc dãy tỉ số bằng nhau ta có \(\dfrac{x}{33}=\dfrac{z}{5}=\dfrac{z-x}{5-33}\) = \(\dfrac{-196}{-28}\)=7

⇒ \(x=7\times33=231\);  z = 7\(\times\) 5 = 35;  

y = \(\dfrac{6}{11}x:\dfrac{9}{2}=\dfrac{6}{11}\times231:\dfrac{9}{2}\) = 28

\(x+y+z=\) 231+28+35 = 294

Chọn b.294

Lời giải:
Tổng quãng đường 3 đội sửa được là:

$(221,7+219,9+219,2):2=330,4$ (m)

Độ dài quãng đường đội I sửa: 

$330,4-219,9=110,5$ (m) 

Độ dài quãng đường đội II sửa:

$330,4-219,2=111,2$ (m) 

Độ dài quãng đường đội III sửa:

$330,4-221,7=108,7$ (m)

\(\dfrac{3}{5}:x-\dfrac{1}{5}=\dfrac{2}{7}\\ \Rightarrow\dfrac{3}{5}:x=\dfrac{2}{7}+\dfrac{1}{5}\\ \Rightarrow\dfrac{3}{5}:x=\dfrac{10+7}{35}\\ \Rightarrow x=\dfrac{3}{5}:\dfrac{17}{35}\\ \Rightarrow x=\dfrac{3}{5}\times\dfrac{35}{17}\\ \Rightarrow x=\dfrac{21}{17}\)

Vậy \(x=\dfrac{21}{17}\)

9994

1172

hhh