Tích của một số vô tỉ với một số nguyên dương có thể là số hữu tỉ hoặc vô tỉ, tùy thuộc vào giá trị của số vô tỉ và số nguyên dương.

Nếu số vô tỉ là 0, thì tích của nó với bất kỳ số nguyên dương nào cũng sẽ là 0, một số hữu tỉ.

Nếu số vô tỉ khác 0, thì tích của nó với một số nguyên dương sẽ là một số vô tỉ. Điều này có thể được giải thích bằng cách giả sử tích của số vô tỉ với số nguyên dương là một số hữu tỉ. Khi đó, ta có thể viết số vô tỉ dưới dạng phân số tối giản, tức là tử số và mẫu số không có thể chia hết cho bất kỳ số nguyên dương nào. Nhưng khi nhân số vô tỉ với một số nguyên dương, tử số và mẫu số của phân số tối giản này sẽ được nhân với số nguyên dương đó, và do đó sẽ có thể chia hết cho số nguyên dương đó. Điều này trái với giả sử ban đầu, do đó tích của số vô tỉ với số nguyên dương không thể là một số hữu tỉ.

Vì vậy, tích của một số vô tỉ với một số nguyên dương có thể là số hữu tỉ hoặc vô tỉ, tùy thuộc vào giá trị của số vô tỉ và số nguyên dương

a, Gọi số nguyên dương là a ( a \(\in\) Z⁺) 

Giả sử tích của số vô tỉ với số nguyên dương a là một số hữu tỉ thì tích đó có dạng: \(\dfrac{b}{c}\) ( b; c \(\in\) Z ; c \(\ne\) 0)

Khi đó số vô tỉ bằng: \(\dfrac{b}{c}\) : a = \(\dfrac{b}{c\times a}\) ( là một số hữu tỉ vô lý)

Nên điều giả sử là sai, vậy tích của một số vô tỉ với một số nguyên dương là số vô tỉ.

b, Giả sử chỉ có 1 số vô tỉ thì tích của số hữu tỉ với một số nguyên dương phải là một số hữu tỉ (trái với điều đã chứng minh ở trên)

Nên điều giả sử là sai. Vậy có vô số số vô tỉ 

Sau khi di chuyển 3 khối lệnh, vị trí của nhân vật sẽ là:

Vị trí ban đầu: (0, 0)
Khối lệnh 1: Di chuyển 50
Vị trí sau khối lệnh 1: (0 + 50, 0) = (50, 0)

Khối lệnh 2: Di chuyển -30
Vị trí sau khối lệnh 2: (50, 0 - 30) = (50, -30)

Khối lệnh 3: Di chuyển 20
Vị trí sau khối lệnh 3: (50 + 20, -30) = (70, -30)

Do đó, vị trí của nhân vật sau khi chuyển 3 khối lệnh là (70, -30).

Sai là 40,0

\(\text{∘ Ans}\)

\(\downarrow\)

Bạn đăng CH đúng môn học nha!

`4,`

\(3\dfrac{1}{5}=\dfrac{5\times3+1}{5}=\dfrac{16}{5}\)

\(\Rightarrow C\)

`5,`

Mười sáu đơn vị: `16`

Bốn trăm chín mươi hai phần nghìn: `492`

\(\Rightarrow\) `16,492`

\(\Rightarrow\) `B`

`6,`

\(\dfrac{40}{7}\cdot\dfrac{14}{5}=\dfrac{5\times8}{7}\cdot\dfrac{7\times2}{5}=\dfrac{8}{1}\cdot\dfrac{2}{1}=\dfrac{16}{1}=16\)

\(\Rightarrow\) \(C\)

`7,`

\(2\dfrac{1}{4}=\dfrac{2\times4+1}{4}=\dfrac{9}{4}\)

\(\dfrac{9}{4}\div\dfrac{1}{8}=18\)

Vậy, \(2\dfrac{1}{4}\) gấp `18` lần \(\dfrac{1}{8}\)

\(\Rightarrow B\)

`8,`

Chiều rộng hình chữ nhật là:

\(\dfrac{25}{12}\div\dfrac{5}{3}=\dfrac{5}{4}\left(m\right)\)

Chu vi hình chữ nhật đó là:

\(\left(\dfrac{5}{3}+\dfrac{5}{4}\right)\times2=\dfrac{35}{6}\left(m\right)\)

Ta có: \(\dfrac{35}{6}=\dfrac{\left(35-5\right)\div6}{6}=5\dfrac{5}{6}\)

\(\Rightarrow B.\)

program dem_so_am_duong_0;

uses crt;

var B: array[1..100] of integer;

      i, n, count_am, count_duong, count_0: integer;

begin

      write('Nhap n: ');

      readln(n);

      for i :=1 to n do

      begin

            write('Nhap phan tu B[' , i, ']: ');

            readln(B[i]);

      end;

      count_am :=0;

      count_duong :=0;

      count_0 :=0;

      for i :=1 to n do

      begin

            if B[i] <  0 then 

                  count_am := count_am + 1

            else if B[i] >  0 then 

                  count_duong := count_duong + 1

            else

                  count_0 := count_0 + 1;

      end;

      write('So phan tu am trong mang: ', count_am);

      write('So phan tu duong trong mang: ', count_duong);

      write('So phan tu bang 0 trong mang: ', count_0);

      readln;

end.

là

saiiiiiiiiiiiiiiiiiiiiiiiiiii

sos

C++:
#include <iostream>

#include <cmath>

int main{

int a,b,c; //Nhập giá trị

cin >> a >> b >> c; // lấy giá trị vào máy

int d = max(a,(b,c)); // tìm giá trị lớn nhất
int e = min(a,(b,c)); //tìm giá trị nhỏ nhất

int q = d*e; //tính tích

cout << q; // in ra máy
}

#include <iostream>

#include <cmath>

int main{

int a,b,c; //Nhập giá trị

cin >> a >> b >> c; // lấy giá trị vào máy

int d = max(a,max(b,c)); // tìm giá trị lớn nhất
int e = min(a,max(b,c)); //tìm giá trị nhỏ nhất

int q = d*e; //tính tích

cout << q; // in ra máy
}

xin lỗi ở trên mình viết nhầm

\(\dfrac{15}{19}\times\dfrac{25}{33}-\dfrac{15}{19}\times\dfrac{14}{33}\)

\(=\dfrac{15}{19}\times\left(\dfrac{25}{33}-\dfrac{14}{33}\right)\)

\(=\dfrac{15}{19}\times\dfrac{11}{33}\)

\(=\dfrac{5}{19}\)

Lần sau để đúng môn học nha bạn.

sao ko xuống dòng đc vậy

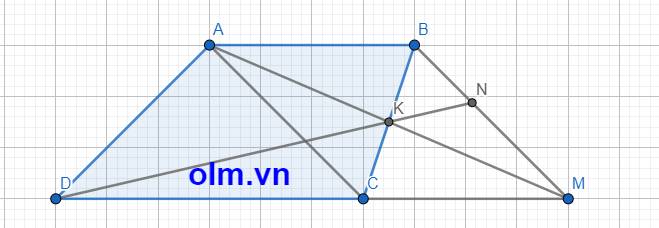
a, Chiều cao hình thang là: (12 + 18): 2 = 15 (cm)

   Diện tích hình thang là:  (18 + 12)\(\times\)15 : 2 = 225 (cm²)

b, Độ dài đoạn CM là: 18 \(\times\) \(\dfrac{2}{3}\) = 12 (cm)

    vậy CM = AB = 12 cm

S_ABM = S_ACM vì (hai tam giác có hai đường cao bằng nhau và hai cạnh đáy tương ứng bằng nhau).

Xét tứ giác ABMC có: AB // CM và AB = CM 

Nên tứ giác ABMC là hình bình hành

Vì K là giao điểm hai đường chéo của hình bình hành nên K là trung điểm của BC vậy KB = KC

Chiều cao của hình thang abcd là:

(18+12):2=15(cm)

a)Diện tích hình thang abcd là:

(18+12)x15:2=225(cm2)

xin lỗi vì mình chỉ giải  được phần a thôi!khi nào giải được thì tôi giải tiếp nhé!