(\(x+1\)) + (\(x-1\))² 

= \(x\) + 1  + \(x^2\) - 2\(x\) + 1

= \(x^2\) - (2\(x\) - \(x\)) + (1 + 1)

= \(x^2\) - \(x\) + 2

\(\left(x+1\right)+\left(x-1\right)^2\\ =\left(x+1\right)+\left(x^2-2x+1\right)\\ =x+1+x^2-2x+1\\ =x^2+\left(x-2x\right)+\left(1+1\right)\\ =x^2-x+2\)

\(a.x^2+4x+4=\left(x+2\right)^2\\ b.x^2-5=\left(x+\sqrt{5}\right)\left(x-\sqrt{5}\right)\\ c.9x^2+6x+1=\left(3x+1\right)^2\\ d.64x^3-27y^3=\left(4x\right)^3-\left(3y\right)^3=\left(4x-3y\right)\left(16x^2+12xy+9y^2\right)\\ e.\left(x+1\right)^2-4y^2=\left(x+1\right)-\left(2y\right)^2=\left(x-2y+1\right)\left(x+2y+1\right)\\ f.8x^3+12x^2+6x+1=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot1+3\cdot2x\cdot1^2+1^3=\left(2x+1\right)^3\)

a, bn xem lại nhé

b, \(x^2-5=\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)\)

c, \(9x^2+6x+1=\left(3x\right)^2+2.3x+1=\left(3x+1\right)^2\)

d, \(64x^3-27y^3=\left(4x\right)^3-\left(3y\right)^3=\left(4x-3y\right)\left(16x^2+12xy+9y^2\right)\)

e, \(\left(x+1\right)^2-4y^2=\left(x+1-2y\right)\left(x+1+2y\right)\)

f, \(8x^3+12x^2+6x+1=\left(2x\right)^3+3.\left(2x\right)^2+3.2x.1^2+1=\left(2x+1\right)^3\)

g, \(6x^2-24y^2=\left(\sqrt{6}x\right)^2-\left(2\sqrt{6}y\right)^2=\left(\sqrt{6}x-2\sqrt{6}y\right)\left(\sqrt{6}x+2\sqrt{6}y\right)\)

h, \(\left(x+y\right)^3+8y^3=\left(x+y+2y\right)\left[\left(x+y\right)^2-2y\left(x+y\right)+4y^2\right]\)

\(=\left(x+3y\right)\left(x^2+3y^2\right)\)

k, \(1975x^4-1975x^2=1975x^2\left(x^2-1\right)=1975x^2\left(x-1\right)\left(x+1\right)\)

i, \(x^3-4x=x\left(x^2-4\right)=x\left(x-2\right)\left(x+2\right)\)

m, \(x^4-2x^3+x^2=x^2\left(x^2-2x+1\right)=x^2\left(x-1\right)^2\)

Hướng giải:

Dễ dàng chứng minh được ADME là hình chữ nhật => DM=AE

Dễ dàng chứng minh được tg EMC cân tại E => EM=EC

=> DM+EM=AE+EC=AC=4 cm không đổi

\(S_{ADME}=EM.DM\)

Hai số coa tổng không đổi thì tích của chúng lớn nhất khi 2 số bằng nhau => \(S_{ADME}\) lớn nhất khi EM=DM

Khi đó sẽ c/m được M là trung điểm của BC

 3x²-75=0                                                                                                 3x²=0+75                                                                                       3x²=75                                                                                                x²=75:3                                                                                                x²=25                                                                                              x²=5²                                                                                                    x=5                                                                                                          Vậy x=5

          \(3x^2-75=0\)

     \(3\left(x^2-25\right)=0\)

        \(x^2-25^2=0\)

\(\left(x-5\right)\left(x+5\right)=0\)

\(\left[{}\begin{matrix}x-5=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-5\end{matrix}\right.\)

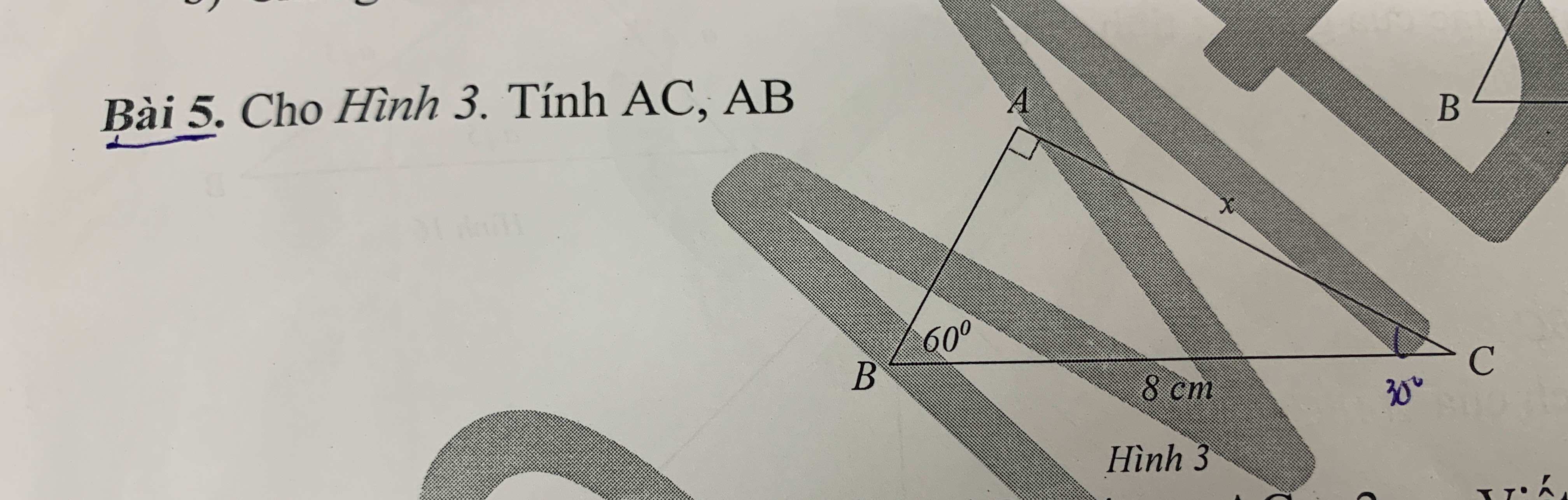
ΔABC vuông tại A nên ta có:

\(sinB=\dfrac{AC}{BC}\\ =>AC=BC\cdot sinB=8\cdot sin60^o=4\sqrt{3}\left(cm\right)\)

Áp dụng định lý Pythagore cho tam giác ABC ta có:

\(BC^2=AC^2+AB^2\\ =>AB=\sqrt{BC^2-AC^2}\\ =>AB=\sqrt{8^2-\left(4\sqrt{3}\right)^2}=4\left(cm\right)\) 

\(a.\left(x+y\right)^2+\left(x-y\right)^2\\ =x^2+2xy+y^2+x^2-2xy+y^2\\ =2x^2+2y^2\\ b.\left(x-y\right)^2-\left(x+y\right)^2\\ =x^2-2xy+y^2-x^2-2xy-y^2\\ =-4xy\\ c.2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2+\left(x-y\right)^2\\ =2\left(x^2-y^2\right)+\left(x^2+2xy+y^2\right)+\left(x^2-2xy+y^2\right)\\ =2x^2-2y^2+x^2+2xy+y^2+x^2-2xy+y^2\\ =4x^2\\ d.\left(x+y\right)^2-4xy-\left(x-y\right)^2\\ =x^2+2xy+y^2-4xy-x^2+2xy-y^2\\ =0\\ e.\left(x-2y\right)\left(x+2y\right)+\left(x+2y\right)^2\\ =x^2-4y^2+x^2+4xy+4y^2\\ =2x^2+4xy\)

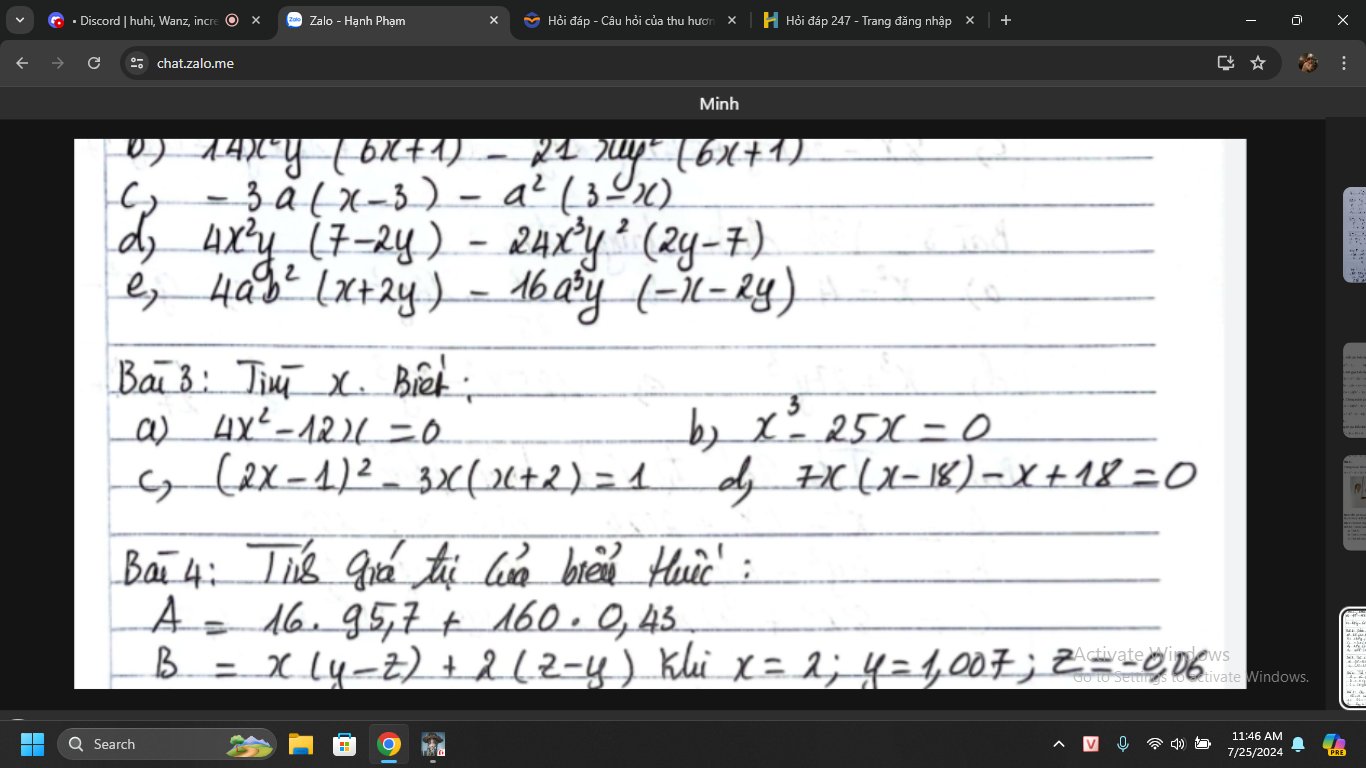
Bài 3:

\(a.4x^2-12x=0\\ \Leftrightarrow4x\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}4x=0\\x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\\ b.x^3-25x=0\\ \Leftrightarrow x\left(x^2-25\right)=0\\ \Leftrightarrow x\left(x-5\right)\left(x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\\ c.\left(2x-1\right)^2-3x\left(x+2\right)=1\\ \Leftrightarrow4x^2-4x+1-3x^2-6x=1\\ \Leftrightarrow x^2-10x+1=1\\ \Leftrightarrow x^2-10x=0\\ \Leftrightarrow x\left(x-10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-10=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=10\end{matrix}\right.\\ d.7x\left(x-18\right)-x+18=0\\ \Leftrightarrow7x\left(x-18\right)-\left(x-18\right)=0\\ \Leftrightarrow\left(x-18\right)\left(7x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-18=0\\7x-1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=18\\7x=1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=18\\x=\dfrac{1}{7}\end{matrix}\right.\)