viết đoạn văn 200 chữ phân tích nhân vật Kỳ Phát trong "Ngôi nhà cổ" của tác giả Phạm Cao Củng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a; 3\(x\) = 2y và \(xy=54\)
\(3x=2y\) ⇒ \(\frac{x}{2}=\frac{y}{3}\) = k ⇒\(x=2k;y=3k\)
Thay \(x=2k;y=3k\) vào biểu thức \(xy\) = 54
Ta có: 2k.2k = 54 ⇒k.k = 54: (2 x 3)
k\(^2\) = 54 : 6
k\(^2\) = 9
\(\left[\begin{array}{l}k=-3\\ k=3\end{array}\right.\)
Nếu k = -3 ta có:
\(\begin{cases}x=2.\left(-3\right)\\ y=3.\left(-3\right)\end{cases}\)
\(\begin{cases}x=-6\\ y=-9\end{cases}\)
Nếu k = 3 ta có: \(\begin{cases}x=2.3\\ y=3.3\end{cases}\)
\(\begin{cases}x=6\\ y=9\end{cases}\)
Vậy (\(x;y\)) = (-6; -9); (6; 9)

Hi, my name is Duc. I'm from [thành phố, quốc gia]. I am [tuổi của bạn] years old. I love [sở thích của bạn], and I enjoy [một số hoạt động]. I am friendly, hardworking, and always open to learning new things. Nice to meet you!

Đoạn văn: Tết đến, làng quê nhộn nhịp trong không khí xuân đầy sắc màu. Mọi người đều quay quần bên nhau, làm mâm cơm cúng ông bà, cha mẹ và tổ tiên. Dọc theo con đường làng, những cây mai, đào nở hoa, đua nhau khoe sắc thắm. Hương bánh chưng thơm ngào ngạt trong mỗi ngôi nhà, hòa cùng tiếng cười rộn rã của trẻ con. Chợ Tết thật đông đúc, tiếng rao hàng của người bán, tiếng chúc Tết của mọi người vang vọng khắp nơi. Đây là thời khắc thiêng liêng để mọi người thể hiện lòng kính trọng với tổ tiên và hy vọng một năm mới an lành, hạnh phúc. Giải thích yêu cầu:
Dấu câu: Trong đoạn văn có sử dụng các dấu câu như dấu chấm (.), dấu phẩy (,), dấu chấm phẩy (;), dấu hai chấm (:), dấu hỏi (?)… để thể hiện sự kết nối các câu, làm rõ ý nghĩa và tạo nhịp điệu cho đoạn văn. Biện pháp tu từ: Đoạn văn sử dụng biện pháp nhân hóa khi mô tả cảnh vật như cây mai, đào "đua nhau khoe sắc thắm", giúp làm nổi bật sự sống động của mùa xuân. Cụm danh từ: Ví dụ, "mâm cơm cúng ông bà, cha mẹ và tổ tiên" hay "hương bánh chưng", "tiếng cười rộn rã", các cụm danh từ này làm rõ ý và tạo sự liên kết trong câu. Động từ: Các động từ như "quay quần", "làm", "nở", "khoe", "thơm", "hòa", "rao", "chúc" giúp diễn tả hành động trong một ngày Tết. Tính từ: Tính từ "đầy sắc màu", "thắm", "ngào ngạt", "rộn rã", "thiêng liêng", "an lành", "hạnh phúc" làm nổi bật vẻ đẹp, không khí và cảm xúc trong những ngày Tết ở làng quê.

“Mẹ yêu ơi! Con yêu mẹ nhiều Mẹ luôn là Phật sống của đời con Mẹ cho con tình yêu cao quý Mẹ là lý trí của đời con.” Đó là những câu hát chạm đến đáy lòng em, và thể hiện được những tình cảm tha thiết nhất mà em dành cho mẹ của mình. Mẹ em là một công nhân hết sức bình thường như bao người khác. Thế nhưng, đối với em thì mẹ là duy nhất và hết sức vĩ đại. Mỗi ngày mẹ thức dậy từ sớm để chuẩn bị bữa sáng cho cả nhà. Sau khi đi làm về, mẹ bận rộn với những công việc nhà như dọn dẹp, giặt giũ, nấu ăn… Thế nhưng mẹ không hề than thở hay cáu gắt với mọi người. Và mẹ luôn dành thời gian để tâm sự, trò chuyện cùng em. Mẹ luôn ở bên cạnh em những lúc em cần nhất. Để tin tưởng, cổ vũ, động viên vô kiện. Thế nên, em luôn tin yêu mẹ, sẵn sàng chia sẻ với mẹ mọi điều. Đối với em, mẹ không chỉ là một người mẹ, mà còn là một người chị, một người bạn. Em luôn yêu thương, quan tâm đến mẹ bằng cả trái tim mình. Thế nên, em luôn cố gắng để trở thành một đứa con ngoan, chăm chỉ để mẹ được vui lòng.

Tỉ số độ dài giữa hai tấm vải:
\(\dfrac{1}{2}:\dfrac{1}{3}=\dfrac{3}{2}\)
Tổng số phần bằng nhau:
\(3+2=5\) (phần)
Tấm vải thứ nhất dài:
\(125:5\times2=50\left(m\right)\)
Tấm vải thứ hai dài:
\(125-50=75\left(m\right)\)
gọi x (m) và y (m) lần lượt là độ dài của tấm vải thứ nhất và tấm vải thứ 2
theo đề 2 tấm dài 125m nên: x + y = 125 (m)
Một nửa tấm vải thứ nhất bằng một phần ba tấm vải thứ hai nên:
\(\dfrac{x}{2}=\dfrac{y}{3}\Leftrightarrow\dfrac{1}{2}\cdot x-\dfrac{1}{3}\cdot y=0\left(2\right)\)
từ (1)(2) TA CÓ: \(\left\{{}\begin{matrix}x+y=125\\\dfrac{1}{2}x-\dfrac{1}{3}y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=50\left(m\right)\\y=75\left(m\right)\end{matrix}\right.\)
vậy tấm vải thứ nhất dài 50m; tấm vải thứ 2 dài 75m

Để làm được câu khó thì con cần có nền tảng vững chắc kiến thức cơ bản, luyện tập thường xuyên, các bài, dạng bài cho đến khi thuần thục. Sau đó đưa các dạng bài nâng cao về dạng bài cơ bản để làm.

Ngày Tết luôn mang lại cho tôi những cảm xúc đặc biệt mà không thể tìm thấy ở bất kỳ ngày nào khác trong năm. Từ những ngày trước Tết, không khí đã rộn ràng khắp nơi. Những cánh mai, cánh đào nở rực rỡ, báo hiệu mùa xuân về. Từ sáng sớm, không khí se lạnh của mùa đông dần nhường chỗ cho sự ấm áp của niềm vui đón Tết. Cả gia đình cùng nhau quây quần bên mâm cơm, dọn dẹp nhà cửa, chuẩn bị những món ăn truyền thống như bánh chưng, dưa hành, và thịt mỡ. Tết là lúc để mọi người nhớ về tổ tiên, thể hiện lòng thành kính qua những lễ cúng. Tuy vậy, điều làm tôi hạnh phúc nhất chính là sự đoàn viên, khi mọi người dù đi xa đến đâu cũng trở về để cùng chia sẻ niềm vui. Tôi luôn cảm thấy rất ấm áp khi được sum vầy cùng gia đình, và niềm vui như được nhân lên khi được gửi những lời chúc tốt đẹp đến mọi người. Mỗi năm, Tết đến là một cơ hội để tôi cùng những người thân yêu tạo ra những kỷ niệm đáng nhớ.

A = \(\frac{9^{14}\times25^5\times8^7}{18^{12}\times625^2\times24^3}\)
A = \(\frac{\left(3^2\right)^{14}\times\left(5^2\right)^5\times\left(2^3\right)7}{\left(2.3^2\right)^{12}\times\left(5^4\right)^3\times\left(2^3.3\right)^3}\)
A = \(\frac{3^{28}\times5^{10}\times2^{21}}{2^{12}\times3^{24}\times5^{12}\times2^9\times3^3}\)
A = \(\frac{3^{28}\times5^{10}\times2^{21}}{\left(3^{24}.3^3\right)\times5^{12}\times\left(2^{12}\times2^9\right)}\)
A = \(\frac{3^{28}\times5^{10}\times2^{21}}{3^{27}\times5^{12}\times2^{21}}\)
A = \(\frac{3}{5^2}\)
A = \(\frac{3}{25}\)
\(\dfrac{9^{14}\cdot25^5\cdot8^7}{18^{12}\cdot625^3\cdot24^3}\)
\(=\dfrac{3^{28}\cdot5^{10}\cdot2^{21}}{\left(2\cdot3^2\right)^{12}\cdot\left(5^4\right)^3\cdot\left(2^3\cdot3\right)^3}\)
\(=\dfrac{2^{21}\cdot3^{28}\cdot5^{10}}{2^{12}\cdot3^{24}\cdot5^{12}\cdot2^9\cdot3^3}\)
\(=\dfrac{2^{21}}{2^{21}}\cdot\dfrac{3^{28}}{3^{27}}\cdot\dfrac{5^{10}}{5^{12}}=\dfrac{3}{5^2}=\dfrac{3}{25}\)
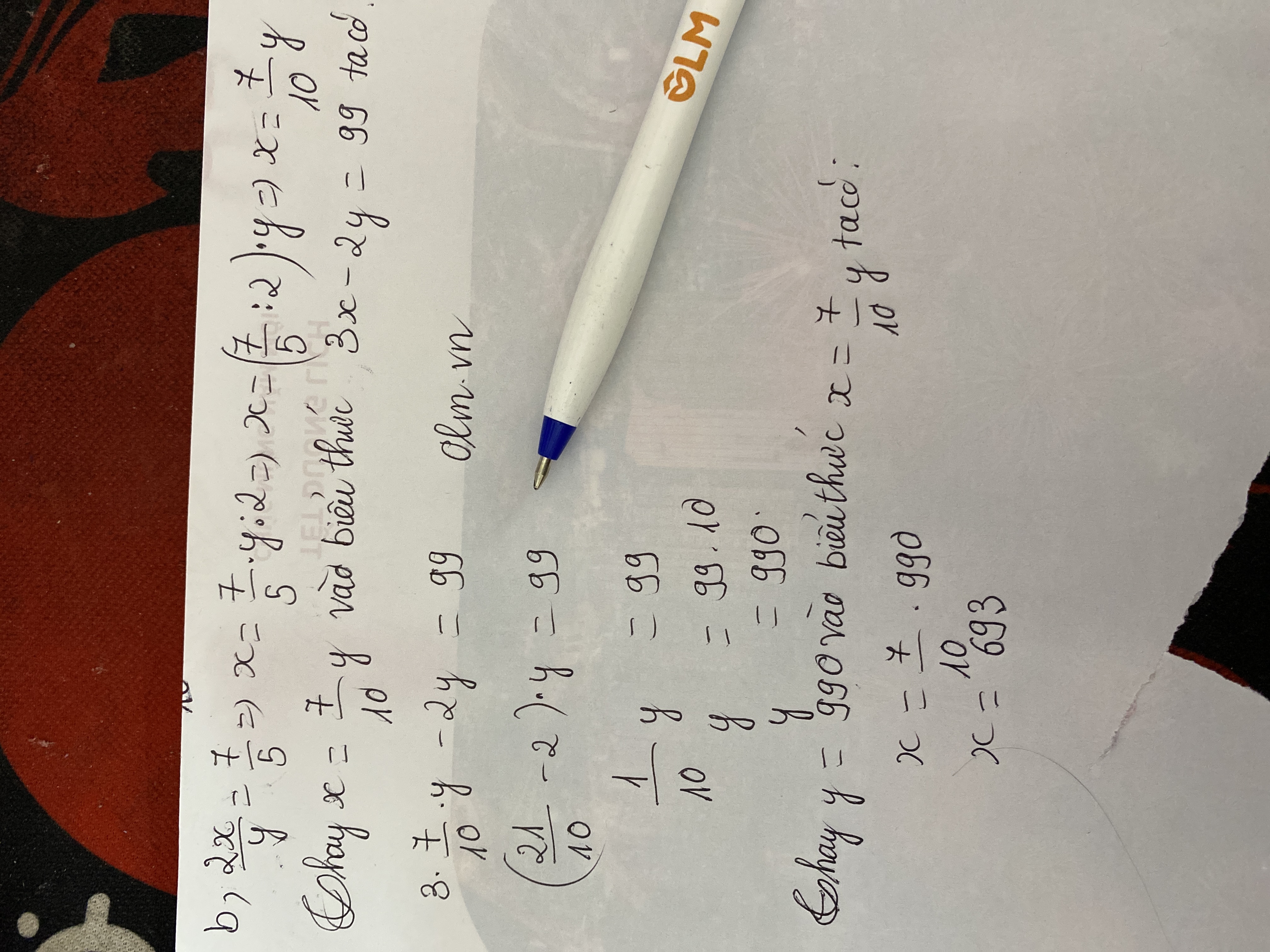

Kỳ Phát, nhân vật chính trong "Ngôi nhà cổ", là một cá thể phức tạp với mối liên kết sâu sắc với ngôi nhà cổ kính. Anh ta như một mảnh ghép không thể thiếu trong bức tranh tổng thể của căn nhà, mang trong mình những bí mật và câu chuyện riêng. Kỳ Phát không chỉ đơn thuần là người thừa kế, mà còn là người bảo vệ những giá trị văn hóa, lịch sử mà ngôi nhà mang lại. Qua từng trang sách, ta thấy Kỳ Phát đối mặt với những thử thách, khám phá những bí ẩn, và dần trưởng thành. Ngôi nhà cổ không chỉ là một không gian vật lý, mà còn là nơi trú ẩn, là nơi giúp Kỳ Phát tìm thấy chính mình.