Bài học cùng chủ đề
- Vị trí tương đối giữa hai mặt phẳng
- Định lí Ta - lét trong không gian
- Hình lăng trụ. Hình hộp. Hình chóp cụt
- Hai mặt phẳng song song (cơ bản)
- Hai mặt phẳng song song (nâng cao)
- Ôn tập: Chứng minh hai mặt phẳng song song
- Ôn tập: Chứng minh hai mặt phẳng song song
- Phiếu bài tập: Hai mặt phẳng song song
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Vị trí tương đối giữa hai mặt phẳng SVIP
Tải đề xuống bằng file Word
Video Player
Video đang được phát tiếp từ điểm dừng lần trước...
Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):

Khẳng định nào sai về hai mặt phẳng (ABCD) và (ACD) ?
A
(ACD) và (ABCD) là hai mặt phẳng phân biệt.
B
(ACD) và (ABCD) có vô số điểm chung.
C
Tất cả các điểm thuộc (ACD) và (ABCD) đều đồng phẳng.
D
Hai mặt phẳng (ACD) và (ABCD) trùng nhau.
Câu 2 (1đ):
Những trường hợp nào sau đây, hai mặt phẳng (P) và (Q) song song?
 |
 |
 |
 |
 |
 |
Câu 3 (1đ):
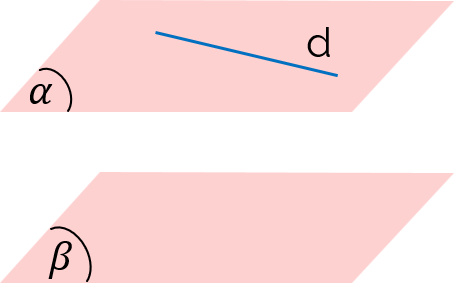
Cho hai mặt phẳng (α) và (β) song song.
Đường thẳng d⊂(α).
Khẳng định nào sau đây là đúng?
A
d⊂(β).
B
d cắt (β) tại điểm duy nhất.
C
d và (β) không có điểm chung.
Câu 4 (1đ):

Cho a⊂(α)
a // (β)
Giả sử (α) không song song với (β) thì khả năng nào không thể xảy ra?
(α) và (β) cắt nhau.
(α) và (β) trùng nhau.
Câu 5 (1đ):
.png)
Giả sử
(α)∩(β)=c
b⊂(α)
b // (β) thì
b và c cắt nhau.
b và c chéo nhau.
b và c song song.
b và c trùng nhau.
Câu 6 (1đ):

Trong không gian, qua điểm A nằm ngoài đường thẳng d thì khẳng định nào sau đây là đúng?
A
Có một và chỉ một đường thẳng qua A và song song với d
B
Có đúng 2 đường thẳng qua A và song song với d.
C
Không có đường thẳng nào qua A và song song với d
D
Có vô số đường thẳng qua A và song song với d
Câu 7 (1đ):

Hai mặt phẳng phân biệt (ABCD) và (ABEF)
Với giả thiết
AF // BE
AF⊂(ADF) thì
BE⊂(ADF)
AF // (BCE).
BE // (ADF).
AF⊂(BCE)
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin chào mừng kem đã quay trở lại với
- khóa học Toán lớp 11 chiến tranh online
- mel.vn hôm nay chúng ta lại tiếp tục với
- những nội dung của hình học không gian
- lớp 11 và trong các bài học trước ta đã
- tìm hiểu về quan hệ song song giữa các
- đường thẳng ở trong không gian cũng như
- giữa một đường thẳng với một mặt phẳng
- vậy giữa hai mặt phẳng trong không gian
- mối quan hệ song song của chúng sẽ có
- những đặc điểm tính chất như thế nào bài
- học ngày hôm nay của chúng ta sẽ trả lời
- cho câu hỏi đó nhưng trước đổ ta hãy tìm
- hiểu về vị trí tương đối của hai mặt
- phẳng cũng giống như một đường thẳng với
- một mặt phẳng ta có hai mặt phẳng trùng
- nhau song song hoặc là cắt nhau với hai
- mặt phẳng trùng nhau chúng ta cũng đã
- làm quen rất nhiều ví dụ thấy có mặt
- phẳng ABCD vậy mặt phẳng acd với mặt
- phẳng ABCD sẽ không có điểm chung có một
- điểm chung Hai có vô số điểm chung Chính
- xác Ở đây Ae
- ý là 4 điểm đồng phẳng sơ đó mặt phẳng
- acd sẽ trùng với mặt phẳng ABCD chúng có
- vô số điểm chung vị trí tương đối thứ
- hai đó là p&q cắt nhau chúng ta cũng đã
- làm quen cụ thể là ở bài tìm giao tuyến
- của 2 mặt phẳng ví dụ thầy có mặt phẳng
- ABCD và mặt phẳng abef đây là hàm mặt
- phẳng phân biệt thì chúng sẽ cắt nhau
- theo một giao tuyến giao tuyến đó chính
- là đường thẳng AB
- vì vậy còn vị trí cuối cùng vị trí mà
- phê Quy song song với nhau chúng ta sẽ
- đi tìm hiểu ký ở trong bài học ngày hôm
- nay bài số 4 hai mặt phẳng song song về
- hai mặt phẳng song song chúng ta sẽ có
- định nghĩa như sau mặt phẳng Alpha và
- mặt phẳng beta được gọi là song song với
- nhau nếu như chúng không có điểm chung
- nào cả
- ở trong trường hợp trùng nhau thì có vô
- số điểm chung trong trường hợp cắt nhau
- chúng cũng có vô số điểm chung và những
- điểm chung đó thuộc vào giao tuyến của 2
- mặt phẳng Còn trong trường hợp song song
- chúng sẽ không có điểm chung nào cả ví
- dụ như mặt phẳng Alpha khoảng beta đây
- không có nghiệm chung trong thực tế cho
- em cũng có thể lấy được rất nhiều ví dụ
- về hai mặt phẳng song song phạt hai mặt
- phẳng song song thì sẽ có ký hiệu lạ
- Alpha song song với bata hoa cũng là
- chúng ta cũng có thể viết lại beta song
- song với Alpha từ định nghĩa đổ Thuê vẽ
- trả lời cho thầy một câu hỏi nếu như
- thầy lấy một đường thẳng D nằm trong mặt
- phẳng Alpha Alpha và Beta là hai mặt
- phẳng song song với d và bita sẽ có vị
- trí tương đối như thế nào
- và chính xác khi đó Alpha và beta Dong
- song sẽ không có điểm chung vậy đưa
- thẳng d và mặt phẳng beta cũng sẽ không
- có điểm chung nào cả
- và đặc biệt hơn nếu như mặt phẳng Alpha
- không chỉ thiếu một mà chưa hai đường
- thẳng AB cùng song song với mặt phẳng
- beta thì khi đó ta sẽ có kết quả của
- định lí Alpha song song với ta đây là bị
- lý rất quan trọng kết quả của định lí
- chính là phương pháp để chúng ta đi
- chứng minh hai mặt phẳng song song với
- nhau ở đây thấy có mặt phẳng Alpha mặt
- phẳng beta Alpha chứa hai đường thẳng a
- và b sao cho A và B cùng song song với
- mặt phẳng beta khi đó thể gọi M là giao
- điểm của đường thẳng a và đường thẳng B
- Khi mặt phẳng Alpha và mặt phẳng beta sẽ
- song song với nhau với định lý quan
- trọng này bây giờ thầy và kem sẽ đi
- chứng minh lý nhất Yêu cầu là chứng minh
- Alpha song song với bata vậy Thấy sẽ sử
- dụng phương pháp phản chứng ta giả sử
- như Alpha và beta không sau khi đó
- alpha-beta sẽ có vị trí nào trong 2 vị
- trí tương đối
- cho nhau hay là cách nhau chính xác bởi
- vì Alpha chúa a a thì song song với Beta
- cho nên Alpha và beta không thể cùng
- nhau được do đó chúng sẽ cắt nhau theo
- một giao tuyến Giả sử do tiền đó là
- đường thẳng C ta sẽ đi chứng minh điều
- này là mâu thuẫn thế sẽ gợi ý cho tôi sẽ
- thiết ta đã có là a song song với beta
- mà đường thẳng a lại nằm trong mặt phẳng
- Alpha mà Alpha và beta cắt nhau theo
- giao tuyến sai thì ta sẽ có ngay A và
- xây là hai đường thẳng song song do tiền
- chung của Alpha và beta sẽ phải song
- song với ai tương tự kem cho thể biết
- với ba dữ kiện bây song song với beta
- Alpha cũng chứa b và giao tuyến chung
- của Alpha Beta là đường thẳng C thì ta
- sẽ có kết luận gì chính xác khi đổ bê sẽ
- song song với save và thể gọi giao tuyến
- của
- A AB chỉ là điểm M M thuộc vào A A và M
- thuộc vào đường thẳng B kem cho thể biết
- trong các khẳng định sau đây khẳng định
- nào là một khẳng định không chính xác
- điểm M nằm ngoài đường thẳng C thì qua m
- sẽ chỉ có duy nhất một đường thẳng song
- song với xe mà ta lại chứng minh được a
- và b cùng song song với xây AB cùng đi
- qua điểm M điều này là vô lí do nó vào
- nó Alpha song song với beta sau khi
- chứng minh được định lý thì ta sẽ áp
- dụng định lý này vào trong quá trình
- chứng minh hai mặt phẳng song song tên
- chủ yếu là một lần nữa nội dung của định
- lý mặt phẳng Alpha chứa hai đường thẳng
- cắt nhau sao cho hai đường thẳng cùng
- song song với mặt phẳng beta thì hai mặt
- phẳng Alpha biết ax song song với nhau
- thế có ví dụ đầu tiên có hai hình chữ
- nhật ABCD và abef
- em nằm trong hai mặt phẳng phân biệt kem
- hệ chứng minh cho thầy mặt phẳng adf sẽ
- song song với mặt phẳng bcd hình chữ
- nhật ABCD nằm trong mặt phẳng thứ nhất
- abef nằm trong mặt phẳng thứ hai hai mặt
- phẳng phân biệt chứng minh mặt phẳng age
- song song với mặt phẳng p c e e
- khi chúng ta sẽ phải đi xác định hai
- đường thẳng cắt nhau hoặc nằm ở trong
- mặt phẳng AIDS hoặc nằm trong mặt phẳng
- P C thay sẽ làm với mặt phẳng p c tương
- tự kèm có thể làm với mặt phẳng age nhất
- với mất khoảng PC ta tìm hai đường thẳng
- cắt nhau nằm trong mặt phẳng này sao cho
- chúng song song với mặt phẳng age ví dụ
- thì có thể thấy ad song song với BC AD
- thì nằm trong mặt phẳng age BC thì tất
- nhiên sẽ không nằm trong mặt phẳng AIDS
- được
- kể từ đó ta có thể kết luận được làm acc
- song song với mặt phẳng AF và tương tự
- AF nằm trong mặt phẳng adf ta có is cũ
- song song với BE off abs là một hình chữ
- nhật từ hay giết kiện này chúng ta có
- thể đi tới kết luận nào sau đây chính
- xác như vậy be cũng song song với mặt
- phẳng age pc7 chính là hai đường thẳng
- mà chúng ta đang cần xác định hai đường
- thẳng này cùng song song với mặt phẳng
- adf chúng cắt nhau và cùng nằm trong mặt
- phẳng bcd số đó ta đã đủ dữ kiện để kết
- luận mặt phẳng and yet song song với mặt
- phẳng b c theo nội dung của định lí
- thì nó cũng chỉ là cách để chúng ta
- chứng minh hai mặt phẳng song song ở
- trong không gian và sau khi tìm hiểu về
- hai mặt phẳng song song chúng ta sẽ có
- cơ sở để đến với nội dung tiếp theo em
- đã biết về định lý thales ở trong hình
- học phẳng vậy ở trong không gian chúng
- ta có định lí Ta lét hay không em đến
- với nội dung lớn tiếp theo định lí Talet
- ở trong Quốc
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022
