Bài học cùng chủ đề
- Vị trí tương đối giữa hai mặt phẳng
- Định lí Ta - lét trong không gian
- Hình lăng trụ. Hình hộp. Hình chóp cụt
- Hai mặt phẳng song song (cơ bản)
- Hai mặt phẳng song song (nâng cao)
- Ôn tập: Chứng minh hai mặt phẳng song song
- Ôn tập: Chứng minh hai mặt phẳng song song
- Phiếu bài tập: Hai mặt phẳng song song
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Ôn tập: Chứng minh hai mặt phẳng song song SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M,N,P lần lượt là trung điểm của SA, SB, SD
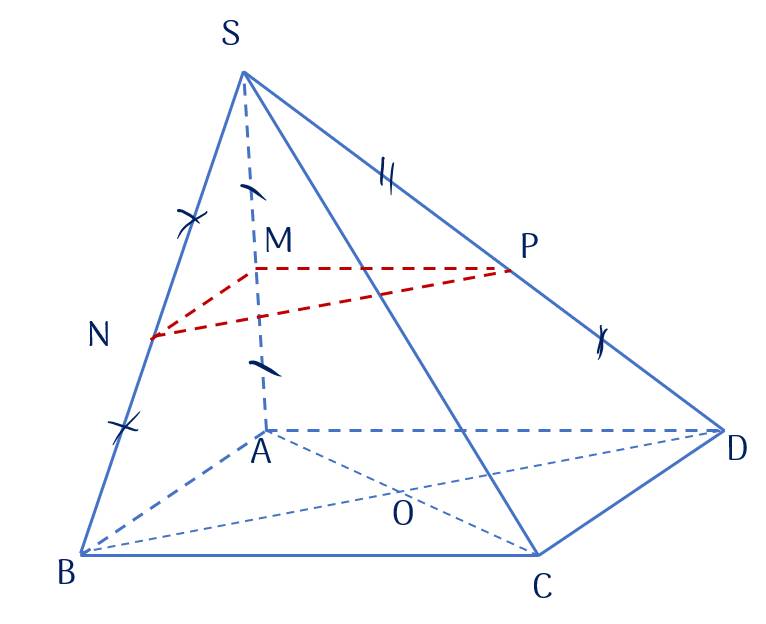
Kéo thả đáp án đúng vào ô trống.
MN // .
NP// .
MP// .
AB AD ACBD
(Kéo thả hoặc click vào để điền)
Câu 2 (1đ):
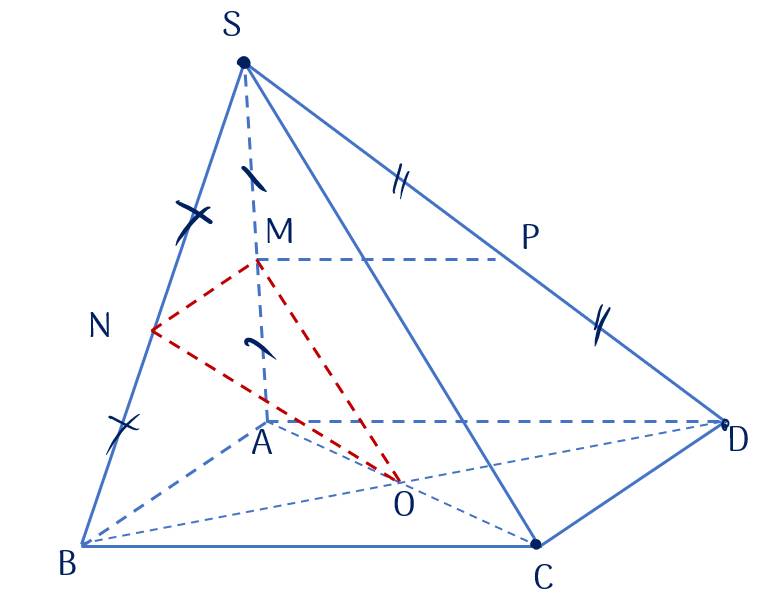
Kéo thả đáp án đúng vào ô trống.
MN // .
ON // .
OM // .
SCCDSD
(Kéo thả hoặc click vào để điền)
Câu 3 (1đ):
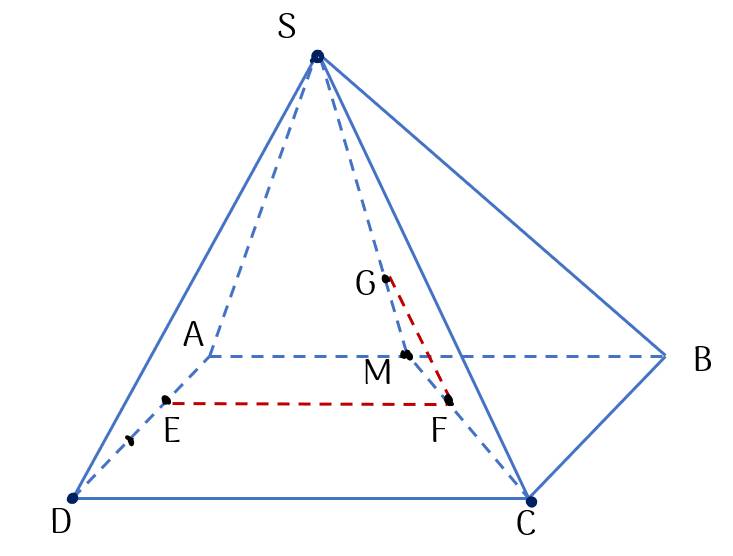
Đường thẳng GF nằm trong mặt phẳng nào?
(ABCD).
(SAB).
(SMC).
(SCD).
Câu 4 (1đ):
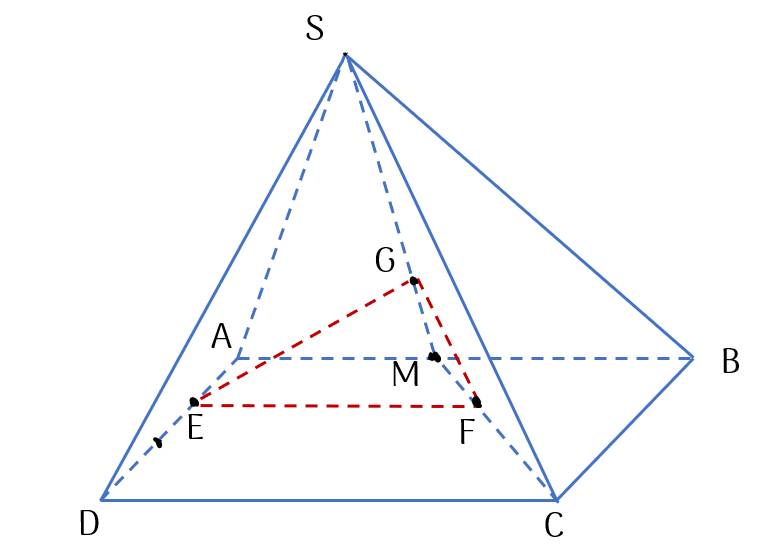
Kéo thả đáp án đúng vào ô trống.
EF // .
GF // .
SDSCDC
(Kéo thả hoặc click vào để điền)
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin chào cây mọc sinh
- sao mày dạo gần đây chúng ta sẽ đi vào
- dạng thứ tư hai mặt phẳng song sau
- một chứng minh hai mặt phẳng song song
- hết thì sẽ nhắc lại lý thuyết
- thì có hai mặt phẳng Alpha và beta như
- thế nào
- trong mặt phẳng Alpha chứa hai đường
- thẳng cắt nhau A và B
- nếu như mặt phẳng ăn xa mà chứa hai
- đường thẳng a và b cắt nhau và a b cùng
- song song với beta thì ta có thể kết
- luận là mặt phẳng Alpha song song với
- mặt phẳng beta
- hơn nữa Nếu được thẳng a song song với
- mặt phẳng b ta khi chứng tỏ phải có một
- đường thẳng a phẩy nằm trong mặt phẳng
- Denta sao cho A phẩy song song với đường
- thẳng a và đường thẳng B cũng song song
- với mặt phẳng beta thì tương tự cũng sẽ
- tồn tại một đường thẳng B phẩy nằm trong
- nó khoảng beta song song với đường thẳng
- b i ê chó đó người ta có điều sau
- nếu Alpha xuống đứng thẳng a và đường
- thẳng d cắt nhau
- và beta cũng chứa hai đường thẳng A phẩy
- B phẩy cắt nhau
- thỏa mãn a song song với hai
- đường thẳng b song song với đường thẳng
- d phẩy thì ta có thể kết luận là mặt
- phẳng Alpha song song với mặt phẳng beta
- như vậy thì để chứng minh mặt phẳng
- Alpha song song mặt phẳng dây ta thì
- chúng ta có thể chỉ ra ở mỗi mặt phẳng
- có hai cặp đường thẳng cắt nhau
- và hai cặp đường thẳng này xong
- để cụ thể hơn về chứng minh hai mặt
- phẳng song sau thì chúng ta sẽ đi làm
- một số bài tập
- bài đầu tiên Cho hình chóp SABCD có đáy
- là hình bình hành tâm O
- M là trung điểm AB A N là trung điểm sb
- Anh tên là trung điểm SD
- thì ta có mặt phẳng pmn ở đây
- đầu tiên để bảo yêu cầu chúng ta chứng
- minh mặt phẳng pmn song song với mặt
- phẳng ABCD
- để chứng minh p MN song song với ABC d
- thì chúng ta cần chỉ ra ở mỗi mặt phẳng
- Sẽ Có 2 cặp đường thẳng cắt nhau
- và chúng song song với nhau
- để chứng minh song song mình chúng ta
- cần nhìn vào cái dữ kiện trung điểm M là
- trung điểm A
- B là trung điểm SD
- và N là trung điểm SB
- thì rõ ràng ta thấy ngay
- là MB sẽ song song với AD Theo định lý
- đường trung bình của tam giác sad MN sẽ
- song song với AB đăng ký đường trung
- bình của tam giác SAB và NP sẽ song song
- với BD Theo định lý đường trung bình tam
- giác SBD
- Uy Nghi Em chỉ cần chọn ra 2 cặp đường
- thẳng thôi là được Có thể ở đây cho bạn
- phẳng MNP thấy sẽ chọn hai đường thẳng
- đó là MN và MP là hai đường thẳng cắt
- nhau tại điểm M
- MN song song với AB và m b song song với
- AD nên trong mặt phẳng ABCD chúng ta sẽ
- chọn giữa hai đường thẳng AB và AD cắt
- nhau tại A
- đây thì ta phải lập luận thêm là do MN
- song song với AB mmb song song với a d
- theo định lương trung bình của tam giác
- và khi chúng ta nên được ra bao nhiêu
- này thì ta hoàn toàn thể kết luận là mặt
- phẳng MNP sẽ song song với mặt phẳng
- ABCD
- tiếp theo là chúng ta cần chứng minh mặt
- phẳng o MN song song với mặt phẳng SCD
- c d e Ừ
- chắc thấy ngay thì om song song với SC
- Theo định lý đường trung bình của tam
- giác ABC
- báo đường sẽ song song với SC Theo định
- lý đường trung bình tam giác SBD còn lại
- thì ta có MN hệ song song với CD cho MN
- song song với AB nên MN + song song với
- CD
- ừ quay đang chị thấy sẽ chọn là hai
- đường thẳng om có n để chứng minh hai
- mặt phẳng song song
- song mặt phẳng M N Thì em cắt on air tại
- điểm O
- tiếp theo là cho mặt phẳng SCD do M
- chúng ta lập luận là song song với FC
- song song với SC tạo song song với SD
- nên chúng ta sẽ chọn SC và SD ở trong
- mặt phẳng SCD bằng hai đường thẳng này
- cắt nhau tại điểm s khi
- chọn giá 200 đường thẳng cắt nhau thì
- chúng ta sẽ nói thêm về phần song sau ra
- mời song song
- ec3n song song SD thì hãy điều này xảy
- ra trực tiếp từ định lý đường trung bình
- của tam giác
- quá khi liên tục ra ba điều này chúng ta
- kết luận là mặt phẳng qua MN song song
- với mặt phẳng SCD
- chúng ta sang bài tiếp theo
- bài 2
- Cho hình chóp SABCD có đáy ABCD là hình
- bình hành
- M là trung điểm AB
- G là trọng tâm tam giác SAB
- chúng ta sẽ chia tại SM là ba phần g.đ
- điểm E nằm trên cạnh AD sao cho AD = 3
- lần AE
- điểm ấy người ta à a = 3 tầng hai
- câu a đường thẳng đi quay song song với
- AB cắt BC tại f
- MC
- đi quay song song với AB cắt BC tại f
- chứng minh GS song song với SC d
- g f song song với SC D F C
- đầu tiên là chúng ta thấy ghép sẽ thu
- mặt phẳng smc mà giao tuyến của mặt
- phẳng smc với mặt phẳng SBC Tính là cạnh
- SC Thế nên thì để chứng minh gf song
- song với SC thì chúng ta sẽ chứng minh
- gf song song với cạnh SC
- như vậy thì chúng ta sẽ cố gắng sử dụng
- định lí Talet ở trong tam giác smc cụ
- thể thì chúng ta có Mg trên Ms bằng 1/3
- ạ Và bây giờ chúng ta cần chứng minh
- msmc bằng 1/3 Điều này hoàn toàn có thể
- chứng minh được bằng cách áp dụng định
- lí Talet ở trong hình thang amcd
- các hình thang abcd có hai đáy là ab và
- DC
- thì ta có ai trên ad = 10 cm C = 1/3
- treo định lí Talet
- Arsenal đây 1/3 là do giả thiết
- khi chúng ta có MF trên MC = 1/3 thì
- chúng ta sẽ xếp tam giác smc
- có Mg trên msmg trên msg msg MC đều bằng
- 1/3 tài này đã dụng định lí Talet thì
- tao suy ra ngay gf song song với FC
- máy C lại thuộc mặt phẳng SCD
- Tiến Andrea ép sẽ song song với mặt
- phẳng SCD à
- a
- tiếp theo chúng ta sang câu b
- Chứng minh rằng Ag song song với sdc
- để chứng minh Ag song song với SCD thì
- các em hoàn toàn có thể rắn đứng thẳng R
- và mặt phẳng s m e
- s m e
- sau chúng ta sẽ tìm giao tuyến giữa SM E
- với mặt phẳng SBC và rồi Chứng minh
- đường thẳng song song với cái dao tiền
- đấy cũng được
- tuy nhiên thì đối với câu bên này chúng
- ta có thể chứng minh r song song với SC
- bằng cách làm cho r thuộc và mặt phẳng
- aef và mặt phẳng gf này sẽ song song với
- mặt phẳng SBC
- cụ thể như sau
- đầu tiên chúng ta cần chứng minh mặt
- phẳng efg song song với mặt phẳng SBC à
- a
- cho mặt phẳng R thì chúng ta sẽ chọn hai
- cạnh là f và f cắt nhau tại f
- f
- ta thấy fg song song với SC và AB song
- song với DC thì trong mặt phẳng SCD sẽ
- chọn hai đường thẳng đó là dc và SC cắt
- nhau tại C Mặt khác do f song song với
- DC
- theo định lí Ta lét ở trong hình thang
- amcd
- EF song song với BC và df song song với
- SC chúng ta chứ nguyên tử có 3
- thì tao hoàn toàn thể kết luận được đó
- là mặt phẳng collector c song song với
- mặt phẳng SCD
- có từ đây mọi đường thẳng thuộc mặt
- phẳng E F G cũng sẽ song song với mặt
- phẳng SCD suy ra đường thẳng r sẽ song
- song với mặt phẳng SCD à
- Anh ta đã đi xong dạng thứ nhất của bà
- chúa Sơn à
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây