Ôn tập: Chứng minh hai mặt phẳng song song SVIP

Hướng dẫn giải:

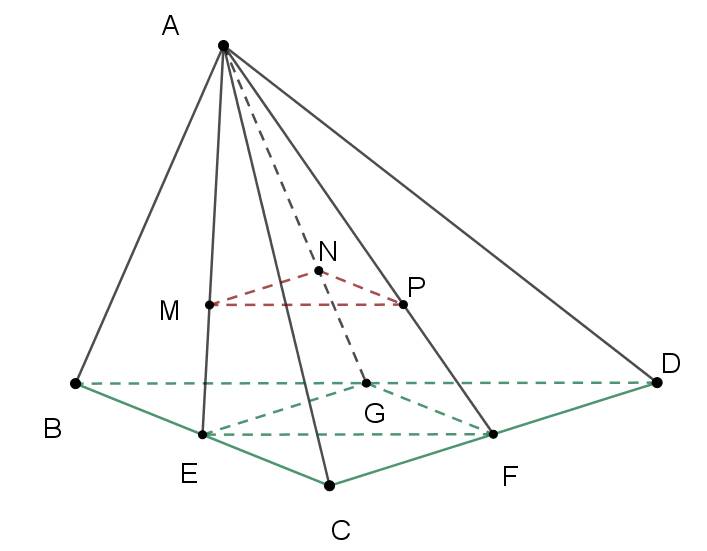
Hướng dẫn. Sử dụng tính chất tỉ số của trọng tâm tam giác để chứng minh.

Gọi E là trung điểm BC, F là trung điểm CD, G là trung điểm BD.

Áp dụng định lý Ta-lét trong tam giác AEF: MP // EF.

Áp dụng định lý Ta-lét trong tam giác AEG: MN // EG.

Vậy (MNP) // (BCD).

Hướng dẫn giải:

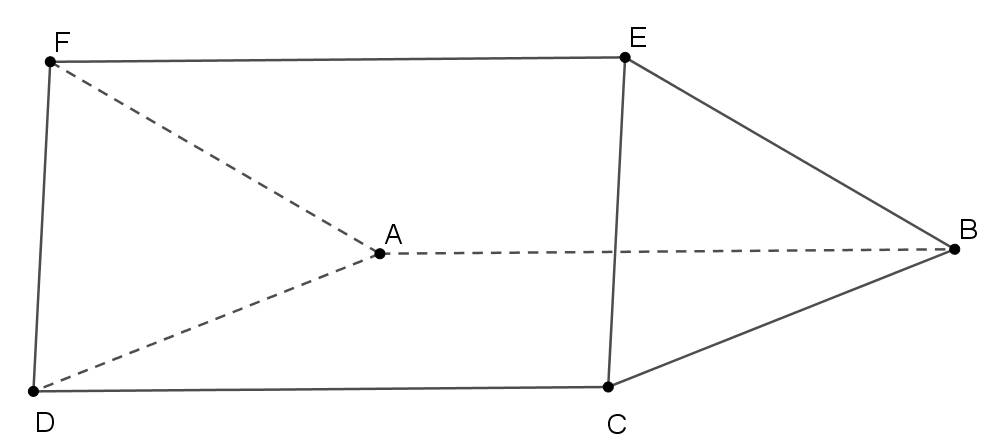
a) AB//EF (do ABEF là hình bình hành), mà EF $\subset$ (CDEF) nên AB//(CDEF).

b) Trong (ADF): AD $\cap$ FA = A

    Trong (BCE): BC $\cap$ BE = B

mặt khác AD//BC và FA//BE. 

Vậy (ADF) // (BCE).

c)

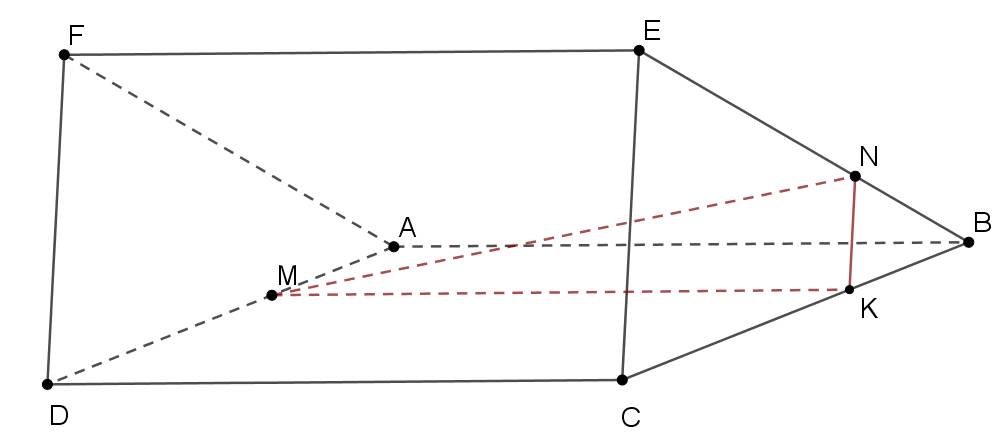
Trong (BEC): Từ N dựng NK song song EC (K thuộc BC). Chứng minh (MNK)//(CDEF) (học sinh tự chứng minh).

Do đó MN luôn song song với mặt phẳng (CDEF).