Bài học cùng chủ đề
- Phương trình bậc hai và cách giải phương trình đặc biệt
- Công thức nghiệm đầy đủ của phương trình bậc hai
- Công thức nghiệm thu gọn của phương trình bậc hai
- Phương trình bậc hai bị khuyết hệ số b hoặc c
- Phương trình bậc hai giải bằng công thức nghiệm
- Phương trình bậc hai chứa tham số
- Tương giao của các đồ thị hàm số
- Bài toán ứng dụng thực tiễn liên quan tới phương trình bậc hai
- Bài toán liên quan đến các yếu tố hình học
- Bài toán liên quan chuyển động
- Phiếu bài tập tuần: Giải toán bằng cách lập phương trình bậc hai
- Bài toán ứng dụng thực tế
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tương giao của các đồ thị hàm số SVIP
Trong mặt phẳng tọa độ $Oxy$, cho hàm số $y=\dfrac14x^2$ có đồ thị $(P)$ và đường thẳng $(d): \, y=-\dfrac12x+2.$
a) Vẽ đồ thị $(P)$ và $(d)$ trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của $(P)$ và $(d)$.
Hướng dẫn giải:
a) Đường thẳng $(d):$
| $x$ | $0$ | $4$ |
| $y = -\dfrac12x + 2$ | $2$ | $0$ |
Parabol $(P)$:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y = \dfrac14x^2$ | $1$ | $\dfrac14$ | $0$ | $\dfrac14$ | $1$ |
Vẽ đồ thị:
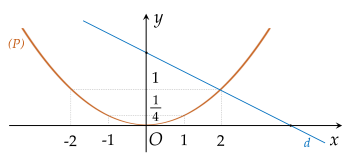
b) Tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép tính.
Hoành độ giao điểm của $(P)$ và $(d)$ là nghiệm của phương trình
$\dfrac14x^2=-\dfrac12x+2$
$x^2+2x-8=0$
$\Delta '=1^2-(-8)=9>0$
Do $\Delta '>0$ nên phương trình đã cho có hai nghiệm phân biệt là $x=-4$ và $x=2$
+ Với $x=-4$ thì $y=4$
+ Với $x=2$ thì $y=1$.
Vậy tọa độ giao điểm của $(P)$ và $(d)$ là $(-4;4)$ và $(2;1)$.
Cho parabol $(P): \, y=2x^2$ và đường thẳng $(d): \, y=x+1$.
a) Vẽ parabol $(P)$ và đường thẳng $d$ trên cùng một hệ trục tọa độ $Oxy$.
b) Tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép tính.
Hướng dẫn giải:
a) Vẽ parabol $(P)$ và đường thẳng $d$ trên cùng một hệ trục tọa độ $Oxy$
Bảng giá trị hàm số $y = 2x^2$:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y = 2x^2$ | $8$ | $2$ | $0$ | $2$ | $8$ |
Đồ thị hàm số $y=2x^2$ là đường cong Parabol đi qua điểm $O$, nhận $Oy$ làm trục đối xứng, bề lõm hướng lên trên.
Đồ thị hàm số $y=x+1$ là đường thẳng đi qua điểm $(0;1)$ và $(-1;0)$
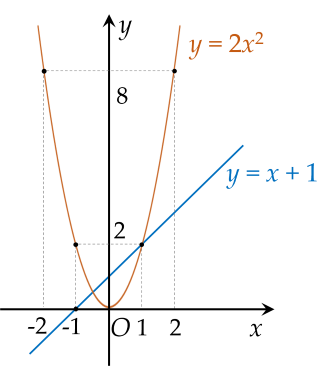
b) Tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép tính.
Hoành độ giao điểm của $(P)$ và $(d)$ là nghiệm của phương trình
$ 2x^2=x+1$
$2x^2-x-1=0$.
Ta có $a+b+c=2-1-1=0$ nên phương trình có hai nghiệm phân biệt $x=1$ và $x=\dfrac{c}{a}=-\dfrac12$.
+ Với $x=1$ thì $y=1+1=2$
+ Với $x=-\dfrac12$ thì $y=-\dfrac12+1=\dfrac12$.
Vậy tọa độ giao điểm của $(P)$ và $(d)$ là $(1;2)$ và $\Big(-\dfrac12;\dfrac12\Big)$.
Cho Parabol $(P): \, y=-x^2$ và đường thẳng $(d)$: $y=5x+6$.
a) Vẽ đồ thị $(P)$.
b) Tìm tọa độ các giao điểm của $(P)$ và $(d)$ bằng phép tính.
Hướng dẫn giải:
a) Vẽ đồ thị $(P)$.
Đồ thị hàm số $y=-x^2$ đi qua gốc tọa độ $O$, có bề lõm hướng xuống và nhận $Oy$ làm trục đối xứng.
Bảng giá trị:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y = -x^2$ | $-4$ | $-1$ | $0$ | $-1$ | $-4$ |
Parabol $(P): \, y=-x^2$ đi qua các điểm $(-2;-4)$, $(-1;-1)$, $(0;0)$, $(1;-1)$, $(2;-4)$.
Đồ thị Parabol $(P): \, y=-x^2$:
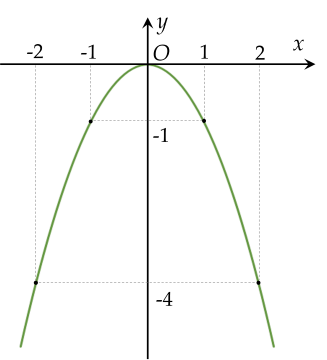
b) Hoành độ giao điểm của đồ thị $(P)$ và $(d)$ là nghiệm của phương trình:
$-x^2=5x+6$
$x^2+5x+6=0$
Ta có: $\Delta=b^2-4ac={{5}^{2}}-4.6=1>0$ nên phương trình có hai nghiệm phân biệt $x_1=\dfrac{-5+1}{2}=-2$; $x_2=\dfrac{-5-1}{2}=-3$.
Với $x_1=-2$ thì $y_1=-{{(-2)}^{2}}=-4$.
Với ${{x}_{2}}=-3$ thì ${{y}_{2}}=-{{(-3)}^{2}}=-9$.
Vậy tọa độ các giao điểm của $(P)$ và $(d)$ là $A(-2;-4)$và $B(-3;-9)$.
Trong mặt phẳng tọa độ $Oxy,$ cho parabol $(P): \, y=2x^2.$
a) Vẽ đồ thị parabol $(P).$
b) Tìm tất cả các điểm thuộc parabol $(P)$ (khác gốc tọa độ $O$) có tung độ gấp hai lần hoành độ.
Hướng dẫn giải:
a) Vẽ đồ thị parabol $(P): \, y=2x^2.$
Bảng giá trị:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y = 2x^2$ | $8$ | $2$ | $0$ | $2$ | $8$ |
Đồ thị:
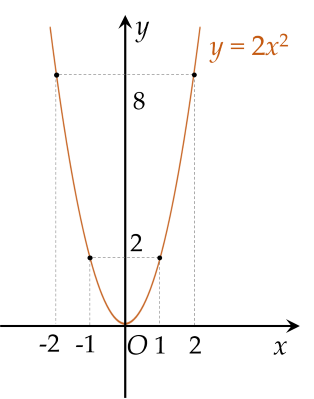
b) Gọi $M(a;b)$ là điểm cần tìm với $a\ne 0;\,b\ne 0$.
Vì $M$ có tung độ gấp hai lần hoành độ nên $b=2a$
Khi đó $M(a ; 2a)$.
Vì $M(a ; 2a)\in (P): \, y=2x^2$ nên: $2a=2a^2$
$2a^2-2a=0$
$a^2-a=0$
$a(a-1)=0$
$a=0$ và $a=1$
Vì $a\ne 0$ nên ta chọn $a=1$.
Vậy $M(1;2)$.
Cho parabol $(P): \, y=x^2$ và đường thẳng $(d): \, y=x+2$.
a) Vẽ parabol $(P)$ và đường thẳng $(d)$ trên cùng một hệ trục tọa độ $Oxy$.
b) Tìm tọa độ giao điểm của parabol $(P)$ và đường thẳng $(d)$ bằng phép tính.
Hướng dẫn giải:
a) Vẽ parabol $(P)$ và đường thẳng $(d)$ trên cùng một hệ trục tọa độ $Oxy$.
+ Xét parabol $(P): \, y=x^2$
Bảng giá trị:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=x^2$ | $4$ | $1$ | $0$ | $1$ | $4$ |
Parabol $(P)$ là đường cong có đỉnh $O(0;0)$, qua các điểm $(1;1), \, (-1;1), \, (2;4), \, (-2;4)$
+ Xét đường thẳng $(d): \, y=x+2$
Đường thẳng $(d)$ cắt trục $Ox$ tại điểm $(-2;0)$, cắt trục $Oy$ tại điểm $(0;2)$
Vẽ parabol $(P)$ và đường thẳng $(d)$ trên cùng một hệ trục tọa độ $Oxy$
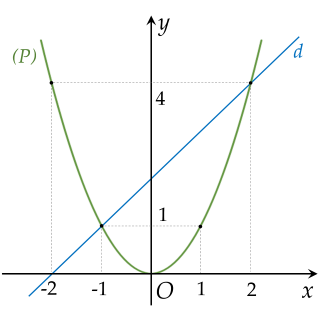
b) Phương trình hoành độ giao điểm của parabol $(P)$ và đường thẳng $(d)$:
$x^2=x+2 $
$x^2-x-2=0$
Ta có $a-b+c=0$nên phương trình có hai nghiệm $x_1=-1 ,\, x_2=-\dfrac{c}{a}=2$
+ Với $x_1=-1$ thì $y_1=-1+2=1$;
+ Với $x_2=2$ thì $y_2=2+2=4$.
Vậy parabol $(P)$ và đường thẳng $(d)$ cắt nhau tại hai điểm $(-1;1)$ và $(2;4)$.
Trong mặt phẳng tọa độ $Oxy$ cho Parabol $(P):y=x^2$, trên $(P)$ lấy hai điểm $A(-1;1),B(3;9)$.
a) Tính diện tích tam giác $OAB$.
b) Xác định điểm $C$ thuộc cung nhỏ $AB$ của $(P)$ sao cho diện tích tam giác $ABC$ lớn nhất.
Hướng dẫn giải:
a) Gọi $y=ax+b$ là phương trình đường thẳng $AB$.
Ta có $\left\{ \begin{aligned} & a.(-1)+b=1 \\ & a.3+b=9 \\ \end{aligned} \right.$
$\left\{ \begin{aligned} & a=2 \\ & b=3 \\ \end{aligned} \right.$
Suy ra phương trình đường thẳng $AB$ là $(d): \, y=2x+3$.
Đường thẳng $AB$ cắt trục $Oy$ tại điểm $I(0;3)$.
(Học sinh tự vẽ hình)
Diện tích tam giác $OAB$ là: $S_{OAB}=S_{OAI}+S_{OBI}=\dfrac12AH.OI+\dfrac12BK.OI$.
Ta có $AH=1; \, BK=3; \, OI=3$.
Suy ra $S_{OAB}=6$ (đvdt).
b) Giả sử $C(c;{{c}^{2}})$ thuộc cung nhỏ $(P)$ với $-1<c<3$.
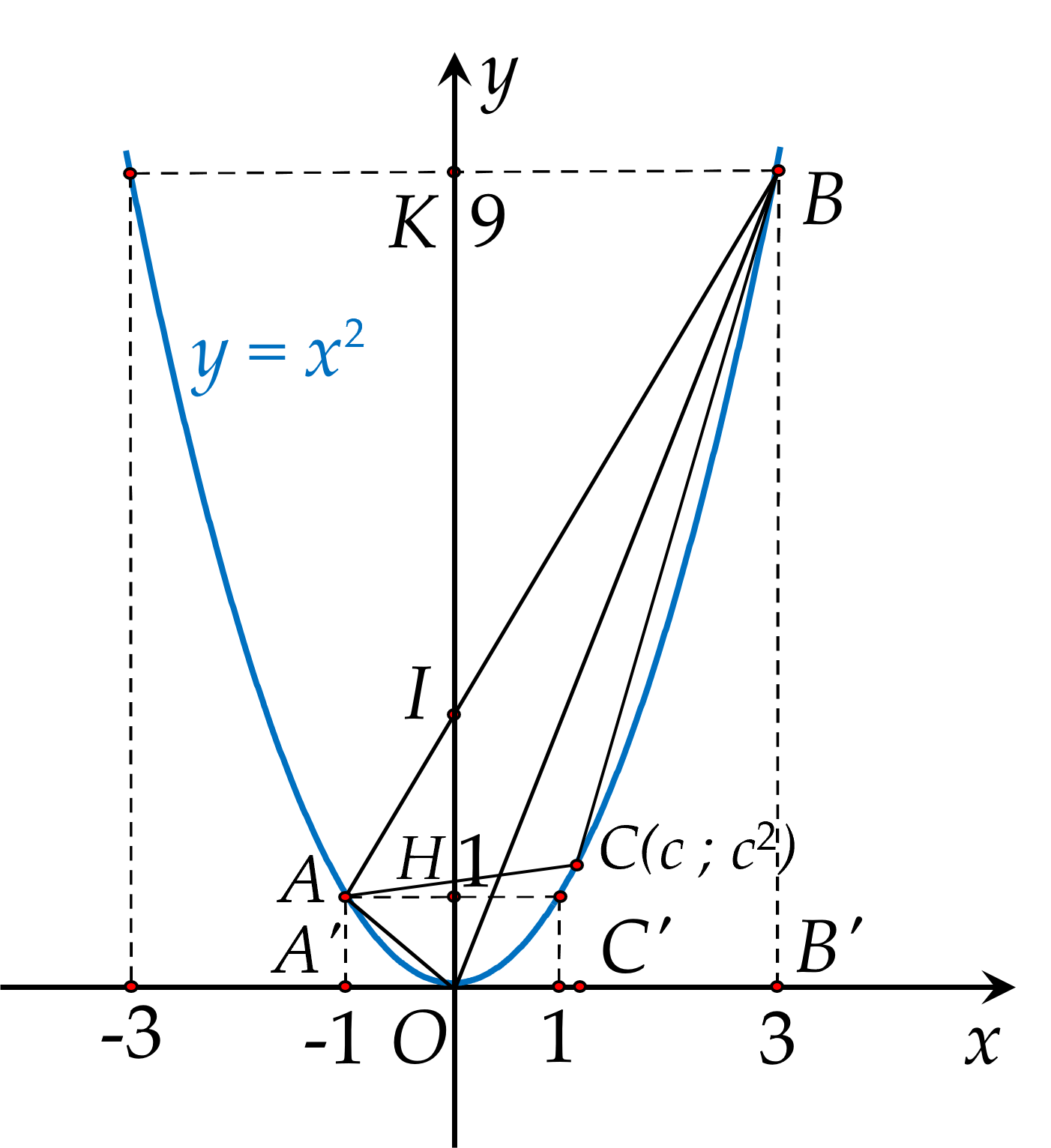
Diện tích tam giác $S_{ABC}=S_{ABB'A'}-S_{ACC'A'}-S_{BCC'B'}$.
Các tứ giác $ABB'A', \, AA'C'C, \, CBB'C'$ đều là hình thang vuông nên ta có:
$S_{ABC}=\dfrac{1+9}{2}.4-\dfrac{1+c^2}{2}.(c+1)-\dfrac{9+c^2}{2}.(3-c)=8-2(c-1)^2 \le 8$.
Vậy diện tích tam giác $ABC$ lớn nhất bằng $8$ (đvdt) khi $C(1;1)$.
