Một số bài tập hình trong các đề kiểm tra giữa kì 1 SVIP

Hướng dẫn giải:

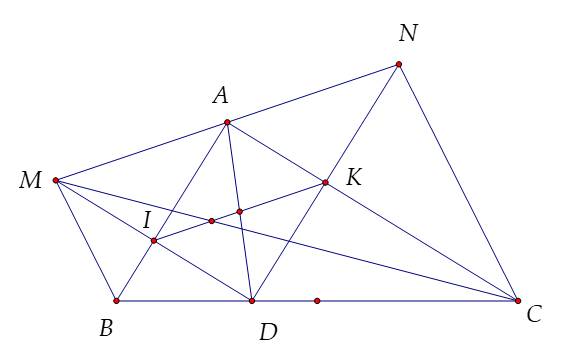
a) Vì M đối xứng D qua AB\[\Rightarrow \]AB là trung trực của MD \[\Rightarrow \] AB \[\bot \] MD tại I

Vì N đối xứng D qua AC\[\Rightarrow \]AC là trung trực của ND \[\Rightarrow \] AC \[\bot \] ND tại K

Xét tứ giác AIMD có:

$\begin{cases}  & \widehat{MIA}=90{}^\circ (MD\bot AB) \\ & \widehat{MHA}=90{}^\circ (ME\bot AC) \\ & \widehat{BAC}=90{}^\circ (gt) \end{cases}$

Vậy AIMH là hình chữ nhật.

b) 

- Chứng minh M, A, N thẳng hàng.

- Chứng minh AM = AN.

c) Tìm được vị trí D là trung điểm của BC.

Hướng dẫn giải:

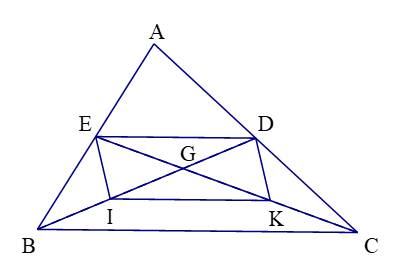
a) Tam giác ABC có:

EA = EB (Vì CE là trung tuyến)

DA = DC (Vì BD là trung tuyến)

Do đó, ED là đường trung bình của tam giác ABC

\(\Rightarrow\left\{{}\begin{matrix}ED=\dfrac{1}{2}BC\\ED//BC\quad\left(1\right)\end{matrix}\right.\)

Vậy ED = 2 (cm).

b) Tam giác BGC có:
IB = IG (gt)
KC = KG (gt)
Do đó, IK là đường trung bình của tam giác BGC
\(\Rightarrow\left\{{}\begin{matrix}IK=\dfrac{1}{2}BC\\IK//BC\end{matrix}\right.\)     (2)
Từ (1) và (2) suy ra ED // IK.

c) Từ (1) và (2) suy ra ED // IK và ED = IK.

Do đó tứ giác EDKI là hình bình hành.

Hướng dẫn giải:

(Hướng dẫn)

a) Tứ giác DEBF là hình bình hành vì có một cặp cạnh đối song song và bằng nhau.

b) Gọi O là giao điểm của AC và BD

- Chỉ ra trong hbh ABCD có O là trung điểm O của AC và BD            (1)

- Chỉ ra trong hbh DEBF có BD cắt EF tại trung điểm của mỗi đường. Mà O là trung điểm của BD nên O là trung điểm của EF          (2)

- Từ (1) và (2) $\Rightarrow $ đpcm.

c) 

- Chỉ ra được M là trọng tâm của $\Delta ABD$ $\Rightarrow OM=\frac{1}{3}OA$

- Chỉ ra được N là trọng tâm của $\Delta BCD$ $\Rightarrow ON=\frac{1}{3}OC$

- Mà $OA=OC\Rightarrow OM=ON$

$\Rightarrow $ đpcm.

Hướng dẫn giải:

a) 

Chứng minh được EF là đường trung bình của tam giác GBC, suy ra EF//=  $\frac{1}{2}$ BC.
Chứng minh được MN // BC và = $\frac{1}{2}$ BC, suy ra MN //= EF.
Vậy MNEF là hình bình hành.

b) 

Hình bình hành MNEF là hình chữ nhật nên NF = EM. Mà EM = $\frac{2}{3}$ BM và NF = $\frac{2}{3}$ NC nên BM = NC.
Vậy Tam giác ABC cân tại A.

c) Hình bình hành MNEF có hai đường chéo BM ⊥ CN . Vậy MNEF là hình thoi.