Giải tam giác (Nâng cao) SVIP

Tam giác $MPQ$ vuông tại $P$. Trên cạnh $MQ$ lấy hai điểm $E,\text{\ \ F}$ sao cho các góc $\widehat{MPE},\text{\ \ }\widehat{EPF},\text{\ \ }\widehat{FPQ}$ bằng nhau. Đặt $MP = q,\ \ PQ = m,\ \ PE = x,\ \ PF = y$. Khẳng định nào sau đây đúng?

Cho góc $xOy$ có số đo $30{^\circ}$. Gọi $A$ và $B$ là hai điểm di động lần lượt trên $Ox$ và $Oy$ sao cho $AB = 1$. Độ dài lớn nhất của đoạn $OB$ bằng

Cho góc $\widehat{xOy} = 30{^\circ}$. Gọi $A$ và $B$ là hai điểm di động lần lượt trên $Ox$ và $Oy$ sao cho $AB = 1$. Khi $OB$ có độ dài lớn nhất thì độ dài của đoạn $OA$ bằng

Tam giác $ABC$ có $AB = c,\ \ BC = a,\ \ CA = b$. Các cạnh $a,\ b,\ c$ liên hệ với nhau bởi đẳng thức $b\left( b^{2} - a^{2} \right) = c\left( a^{2} - c^{2} \right)$. Khi đó góc $\widehat{BAC}$ bằng

Tam giác $ABC$ vuông tại $A$, có $AB = c,\ \ AC = b$. Gọi $\mathcal{l}_{a}$ là độ dài đoạn phân giác trong góc $BAC$. Khẳng định nào sau đây đúng?

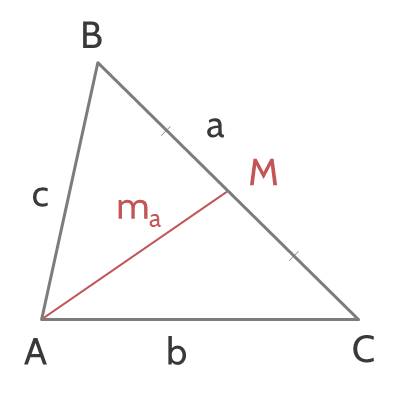
Trong hình vẽ trên, gọi $m_a=AM$ là trung tuyến ứng với cạnh $BC$. Khẳng định nào sau đây đúng?

Tam giác $ABC$ có $AB = c, BC = a, CA = b$ và ba đường trung tuyến $m_a, m_b, m_c$. Gọi G là trọng tâm của tam giác. Cho hai mệnh đề

(1) $m_a ^2 + m_b ^2 + m_c ^2 = \dfrac{3}{4}(a^2 + b^2 + c^2)$;

(2) $GA ^2 + GB ^2 + GC ^2 = \dfrac{1}{3}(a^2 + b^2 + c^2)$.

Xét hai mệnh đề trên,