Bài học cùng chủ đề
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Nam Định năm 2022 - 2023 (Trắc nghiệm)
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Nam Định năm 2022 - 2023 (Tự luận)
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Hà Nội năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Hồ Chí Minh năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Đà Nẵng năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 tỉnh Vĩnh Phúc năm 2022 - 2023
- Đề thi thử trường THCS & THPT Lương Thế Vinh - Hà Nội 2022-2023
- Đề thi tuyển sinh vào lớp 10 THPT Nghệ An năm 2022-2023
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Huế năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Thanh Hóa năm 2022 - 2023
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề và đáp án tuyển sinh vào lớp 10 thành phố Hồ Chí Minh năm 2022 - 2023 SVIP
Cho parabol $(P): y=x^2$ và đường thẳng $(d): y=-x+2$.
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép tính.
Hướng dẫn giải:
a) 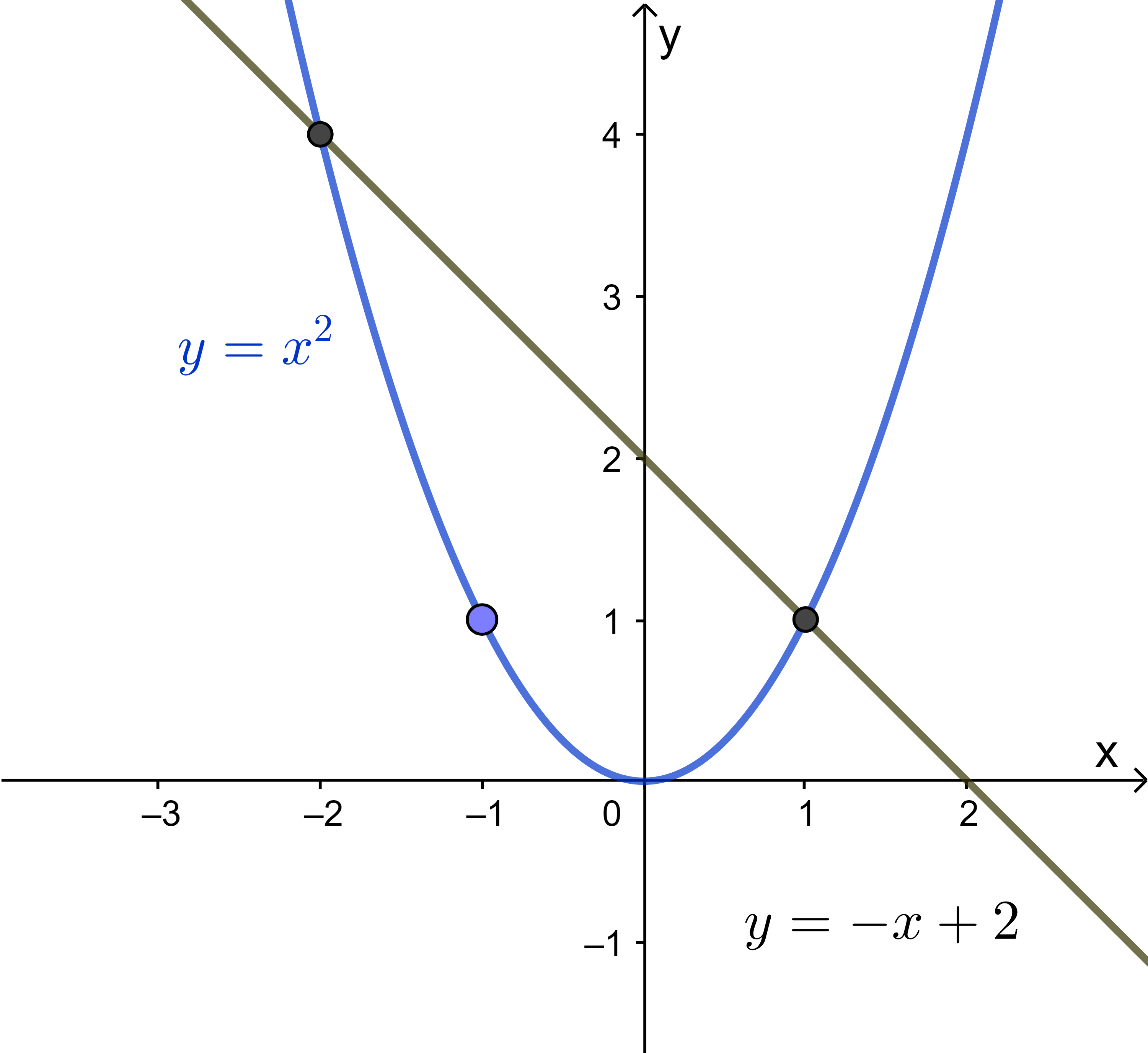
b) Hoành độ giao điểm của $(\mathrm{P})$ và (d) là nghiệm của phương trình $x^2=-x+2 \Leftrightarrow x^2+x-2=0$.
Ta có $a+b+c=1+1+(-2)=0$ nên phương trình có 2 nghiệm phân biệt $\left[\begin{array}{l}x_1=1 \\ x_2=-\dfrac{2}{1}=-2\end{array}\right.$
Vói $x_1=1 \Rightarrow y_1=1^2=1 \Rightarrow A(1 ; 1)$
Vói $x_2=-2 \Rightarrow y_2=(-2)^2=4 \Rightarrow B(-2 ; 4)$.
Vậy tọa độ giao điểm của $(P)$ và $(d)$ là $A(1 ; 1)$ và $B(-2 ; 4)$.
Cho phurong trình $2 x^2-4 x-3=0$ có hai nghiệm $x_1, x_2$.
Không giải phương trinh, hãy tính giả trị của biểu thức $A=\left(x_1-x_2\right)^2$
Hướng dẫn giải:
Ta có: $a c=2 \cdot(-3)=-6<0$ nên phương trình luôn có 2 nghiệm phân biệt trái dấu $x_1, x_2$.
Áp dụng hệ thức Vi-ét ta có: $\left\{\begin{array}{l}x_1+x_2=-\dfrac{-4}{2}=2 \\ x_1 x_2=\dfrac{-3}{2}\end{array}\right.$.
Khi đó ta có:
$\begin{aligned}& A=\left(x_1-x_2\right)^2 \\& A=\left(x_1+x_2\right)^2-4 x_1 x_2 \\& A=2^2-4 \cdot \dfrac{-3}{2} \\& A=4+6 \\& A=10\end{aligned}$
Vậy $A=10$.
Để đánh giá thể trạng (gầy, bình thường, thùra cân) của một người, người ta thường dùng chỉ số $B M I$ (Body Mass Index). Chỉ số BMI dược tính dựa trên chiều cao và cân nặng theo công thức sau:
\(BMI = \dfrac{\text{cân nặng (kg)}}{\text{chiều cao (m) } \times \text{chiều cao (m)}}\)
Đối với người trưởng thành, chỉ số này cho đánh giá như sau:
| Phân loại | BMI (kg/m2) |
| Cân nặng thấp (gầy) | < 18,5 |
| Bình thường | 18,5 - 24,9 |
| Thừa cân | $\ge$ 25 |
| Tiền béo phì | 25 - 29,9 |
| Béo phì độ I | 30 - 34,9 |
| Béo phì độ II | 35 - 39,9 |
| Béo phì độ III | $\ge$ 40 |
Hạnh và Phúc là hai người trưởng thành đan cần xác định thể trạng của mình.
a) Hạnh cân nặng $50kg$ và cao $1,63 \mathrm{~m}$. Hãy cho biết phân loại theo chỉ số BMI của Hạnh? (làm tròn kết quả đến chữ số thâp phân thấp nhất)
b) Phúc cao 1,73 m thì cân năng trong khoảng nào để chỉ số BMI của Phúc đ̛̉ múr bình thường? (làm tròn kết quả đến chữ số thập phân thấp nhất)
Hướng dẫn giải:
a) Chỉ số BMI của Hạnh là: $\dfrac{50}{1,63.1,63} \approx 18,8 \in(18,5 ; 29,4)$.
Vậy chỉ số BMI của Hạnh là bình thường.
b) Ta có: $B M I=\dfrac{\text {cận nặng }(\mathrm{kg})}{\text { chiều cao }(m) \cdot \text { chiều cao }(m)} \Rightarrow$ cân nặng $(\mathrm{kg})=$ BMI. chiều cao $(\mathrm{m})$. chiều cao $(\mathrm{m})$.
Do chỉ số BMI mức bình thường là 25 - 29,9 nên:
Cân nặng tối thiểu của Phúc là: $25.1,73.1,73 \approx 74,8(\mathrm{~kg})$
Cân nặng tối đa của Phúc là: 29,9.1,73.1,73 $\approx 89,5(\mathrm{~kg})$
Vậy cân nặng của Phúc trong khoảng $74,8 \mathrm{~kg}$ đến $89,5 \mathrm{~kg}$ thì chi số BMI của Phúc ở mức bình thường.
Giá bán một cái bánh cùng loại ở hai của hàng $A$ và $B$ đều là 15000 đồng, nhurng mỗi của hàng áp dụng hình thức khuyến mãi khác nhau.
Cửa hàng A: đối vổi 3 cái bánh đầu tiên, giá mỗi cái là 15000 đồng và từ cái bánh thứ tur trổ đi khách hàng chỉ phải trả $75 \%$ giá bán.
Cửa hàng B: cứ mua 3 cái bánh thì được tặng thêm một cái bánh cùng loại.
Bạn Hà̀ng cần đúng 13 cái bánh để tổ chức sinh nhật thì bạn ấy nên mua bánh ở củ̉a hàng nào để tiết kiệm và tiết kiệm đurợc bao nhiêu tiền so với củ̉a hàng kia?
Hướng dẫn giải:
Nếu Hằng mua ở cửa hàng $A$ thì Hằng phải mua 3 cái bánh với giá 15000 đồng/cái và 10 cái bánh với giá $75 \% .15000 /$ cái nên Hằng cần trả số tiền là:
$3.15000+10.15000 .75 \%=157500 \text { (đồng) }$
Nếu Hằng mua ở cửa hàng $B$ thì cứ mua 3 bánh Hằng được tặng 1 cái bánh cùng loại nên nếu Hằng mua 9 bánh thì Hằng được tặng 3 chiếc và thiếu 1 chiếc cần mua với giá 15000 đồng. Như thế, Hằng sẽ cần phải mua 10 cái bánh và số tiền Hằng cần trả là:
$9.15000+15000=150000 \text { (đồng) }$
Vậy bạn Hằng mua bánh ở cửa hàng $B$ thì tiết kiệm hơn và tiết kiệm được $157500-150000=7500$ đồng so với cửa hàng $A$.
Một vận động viên khi leo núi nhận thấy rằng càng lên cao thì nhiệt độ không khí càng giảm. Mối liên hệ giữa nhiệt độ không khi $T$ và độ cao h (so vổi chân nủi) được cho bổi hàm số $T=a . h+b$ có đồ thị nhur hình vễ bên (nhiệt độ $T$ dự̂c tính theo ${ }^{\circ} C$ và độ cao h tinh theo mét)
Tại chân núi, người đó đo được nhiệt độ không khi là $23^{\circ} C$ và trung bình cư lên cao $100 m$ thì nhiệt độ giảm $0,6^{\circ} C$.
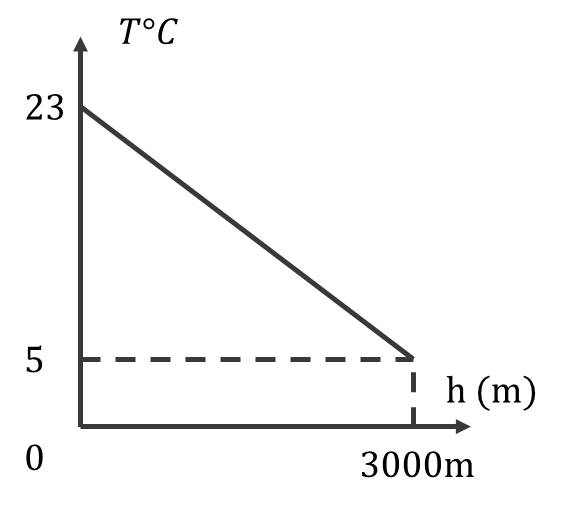
a) Xác định $a,\ b$ trong công thức trên.
b) Bạn Minh đang leo núi và dùng nhiệt kế đo được nhiệt độ không khi tại vị trí dừng chân là $15,8^{\circ} C$. Hỏi bạn Minh đang ở độ cao bao nhiêu mét so vổ chân núi?
Hướng dẫn giải:
a) Cách I:
Ta có: $T=a h+b$.
Quan sát đồ thị hàm số, đường thẳng $T=a h+b$ đi qua điểm $(3000 ; 5)$ nên ta có phương trình:
$3000 a+b=5$
Vì ở chân núi, nhiệt độ không khí là $23^{\circ} C$ nên ta có:
$23=0 a+b \Leftrightarrow b=23$
Thay $b=23$ vào $3000 a+b=5$ ta được:
$3000 a=5-23=-18$
$\Leftrightarrow a=-0,006$
Vậy $a=-0,006$ và $b=23$.
Cách 2:
Tại chân núi, khi đó chiều cao là $h=0(m)$ và nhiệt độ là $23^{\circ} C$ nên $T=23$ suy ra $b=23$.
Vì trung bình cứ lên cao $100 m$ thì nhiệt độ giảm $0,6^{\circ} C$ mà nên ta có:
Ta có:
$\Delta t=T_2-T_1=-0,6 $
$\Delta t=a h_2+b-\left(a h_1+b\right) $
$\Delta t=a\left(h_2-h_1\right) $
$\Delta t=a \cdot 100 $
$\Rightarrow a=-0,6: 100=-0,006 $
Vậy $ a=-0,006 ; b=23$
b) Theo ý a) ta có: $T=-0,006 h+23$.
Bạn Minh đang ờ nhiệt độ $15,8^{\circ} C$ so với chân núi nên thay $T=15,8$ vào $T=-0,006 h+23$ ta có:
$15,8=-0,006 h+23 $
$ \Leftrightarrow-0,006 h=-7,2 $
$\Leftrightarrow h=1200$
Vậy Minh đang ở độ cao $1200 m$ so với chân núi.
Một đống cát dạng hình nón có chu vi đáy là 25,12m và độ cao là 1,5m.
a) Tính thể tích đống cát trên? Biết công thức tính chu vi đường tròn là $C=2\pi R$ và công thức tính thể tích hình nón là $V=\dfrac13 \pi R^2 h$ (trong đó $R$ là bán kính đường tròn đáy; $h$ là chiều cao hình nón, lấy $\pi = 3,14$).
b) Người ta dùng xe cải tiến để vận chuyển đống cát đó đến khu xây dụmg. Biết thùng chứa của xe cải tiến có dạng hình hộp chữ nhật có kích thước dài $1 ~m$, rộng 6dm và cao 3 dm. Trong mỗi chuyến xe, thùng xe cô thể chỉa nhiều hơn thể tích thực của nó là $10 \%$ để vận chuyển đự̛̣c nhiều cát hơn. Höi cần it nhất bao nhiêu chuyến xe cải tiến để chuyển hết đống cát trên?
Hướng dẫn giải:
a)Hình nón có chu vi đáy là $25,12 ~m$ nên ta có:
$C=2 \pi R=25,12 \Rightarrow R=\dfrac{25,12}{2.3,14}=4(~m)$
Thể tích của đống cát trên là:
$V=\dfrac{1}{3} \pi R^2 h=\dfrac{1}{3} \cdot 3,14 \cdot 4^2 \cdot 1,5=25,12\left(m^3\right)$
Vậy thể tích của đống cát là $25,12 m^3$.
b) Đổi $6 d m=0,6 m, 3 d m=0,3 m$
Thể tích của thùng chứa là $1.0,6.0,3=0,18\left(~m^3\right)$
Trong mỗi chuyến xe, thùng xe có thể chứa: $0,18+0,18.10 \%=0,198\left(~m^3\right)$
Gọi $n$ là số chuyến xe tối thiểu để có thể chuyển hết đồng cát.
Khi đó $n=\left[\dfrac{V}{0,198}\right]+1=127$ chuyến.
Đại hội Thể thao Đông Nam A - SEA Games (South East Asian Games) là sự kiện thể thao dự̛̣c tổ chức 2 năm một lần với sự tham gia của các vận động viên trong khu vực Đông Nam Á. Việt Nam là chủ nhà của SEA Games 31 diễn ra từ ngày 12/5/2022 đến ngày 23/5/2022.
Ổ môn bóng đá nam, một bảng đấu gồm có 5 đội $A, B, C, D, E$ thi đấu theo thể thức vòng tròn một lượt (mỗi đội thi đấu đúng một trận với các đội còn lại). Trong mỗi trận đấu, đội thẳng được 3 điểm, đội hòa được 1 điểm và đội thua đurợc 0 điểm.
a) Hỏi có tất cả bao nhiêu trận đấu đã điễn ra ở bảng đấu trên?
b) Khi kết thúc bảng đấu, các đội A, B, C, D, E lần lượt có điểm số là 10, 9, 6, 4, 0. Hỏi có bao nhiêu trận hòa và cho biết đó là trận hòa giũ̃a các đội nào (nếu có)?
Hướng dẫn giải:
a) Đội $A$ thi đấu với 4 đội còn lại $\Rightarrow$ Có 4 trận.
Đội $B$ thi đấu với 3 đội còn lại (vì đội $B$ đã thi đấu với đội $A$ ) $\Rightarrow$ Có 3 trận.
Đội $C$ thi đấu với 2 đội còn lại (vi đội $C$ đã thi đấu với đội $A$ và $B) \Rightarrow$ Có 2 trận.
Đội $D$ thi đấu với 1 đội còn lại (vì đội $D$ đã thi đấu với đội $A, B$ và $C$ ) $\Rightarrow$ Có 1 trận.
Vậy có tất cả $4+3+2+1=10$ (trận).
b) Từ câu a, ta có tất cả 10 trận đấu, trong đó gồm trận thắng - thua và trận hòa.
Gọi số trận thắng - thua là $x$ trận, số trận hòa là $y$ trận (ĐK: $x, y \in \mathbb{N}$ ).
Khi đó ta có: $x+y=10$.
Mỗi trận thắng - thua thì được tổng điểm là 3. Có $x$ trận thắng - thua thì có số điểm là $3 x$.
Mỗi trận hòa thì cả 2 đội trong trận đó được 1 điểm
$\Rightarrow$ Tổng điểm có được trong 1 trận hòa là 2 điểm.
$\Rightarrow y$ trận hòa có $2 y$ điểm.
Tổng số điểm trong tất cả 10 trận đấu trên là $3 x+2 y=10+9+6+4+0=29$.
Vậy ta có hệ phương trình:
$ \left\{\begin{array} { l } { x + y = 1 0 } \\ { 3 x + 2 y = 2 9 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { 2 x + 2 y = 2 0 } \\ { 3 x + 2 y = 2 9 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { x = 9 } \\ { x + y = 1 0 } \end{array} \Leftrightarrow \left\{\begin{array}{l} x=9 \\ y=1 \end{array}(tm)\right.\right.\right.\right. $
$\Rightarrow$ Số trận hòa là 1 trận.
Giả sử đội nào đó có $a$ trận thẳng, 1 trận hòa, và $c$ trận thua.
$\Rightarrow$ Số điểm của đội đó là $3 a+1$ điểm $\Rightarrow$ Điểm của các đội có 1 trận hòa phải là một số chia cho 3 dư 1.
Ta thấy có điểm của đội A và độ D thỏa mãn.
Vậy trận đấu hòa là trận đấu giữa đội A và đội D.
Cho tam giác $A B C$ có 3 góc nhọn nội tiếp dường tròn $(O)(A B<A C$ ). Gọi $D$ là điểm trên cung nhỏ $B C$ sao cho $D B<D C$. Từ $D$ kẻ $D E$ vuông góc với $B C$ (E thuộc $B C$ ), kẻ $D F$ vuông góc vổ $A C$ (F thuộc $A C$ ). Đường thẳng $E F$ cắt tia $A B$ tại $K$.
a) Chứng minh tứ giảc CDEF nội tiếp và $\widehat{ D F E}=\widehat{D A B} $.
b) Chứng minh tứ giác $D K B E$ nội tiếp và $D B \cdot D F=D A \cdot D E$.
c) Gọi I, J lần lượt là trung diểm của $A B, E F$. Chứng minh $I J$ vuông góc vởi $D J$.
Hướng dẫn giải:
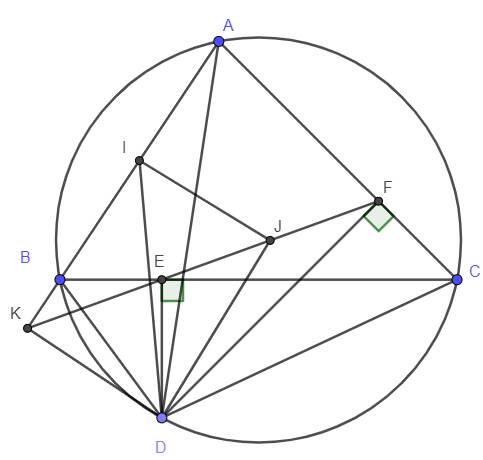
a) Ta có : $D E C=D F C=90^{\circ}$
$\Rightarrow$ Tứ giác CDEF nội tiếp
$\Rightarrow D F E=D C E$
Mà $D C E=D A B$ (cùng chắn $B D)$
Vây $D F E=D A B$
b) Ta có: $D F E=D A B$ (cmt)
$\Rightarrow$ Tứ giác $A K D F$ nội tiếp
$\Rightarrow A K D=90^{\circ}$ Mà $B E D=90^{\circ}$
$\Rightarrow$ Tứ giác $D K B E$ nội tiếp
Xét $\triangle D B A$ và $\triangle D E F$ ta có :
$ \begin{aligned} & B D A=F D E=A C B \text { và } D F E=D A B(\mathrm{cmt}) \\ & \Rightarrow \triangle D B A \backsim \triangle D E F(\mathrm{~g}-\mathrm{g}) \\ & \Rightarrow \frac{D B}{D E}=\frac{D A}{D F} \Rightarrow D B \cdot D F=D A \cdot D E \end{aligned} $
c) Ta có: $\triangle D B A \backsim \triangle D E F(\mathrm{cmt})$
$\Rightarrow \frac{B A}{E F}=\frac{D B}{D E} \Rightarrow \frac{2 B I}{2 E J}=\frac{D B}{D E} $
$\Rightarrow \frac{B I}{E J}=\frac{D B}{D E}$
Mà $D B I=D E J(\triangle D B A \backsim \triangle D E F)$
$\Rightarrow \triangle D B I \backsim \triangle D E J(\mathrm{c}-\mathrm{g}-\mathrm{c})$.
$\Rightarrow B I D=K J D \Rightarrow$ Tứ giác $K I J D$ nội tiếp
$\Rightarrow I J D=180^{\circ}-I K D=90^{\circ} \Rightarrow I J \perp D J$
