Bài học cùng chủ đề
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Nam Định năm 2022 - 2023 (Trắc nghiệm)
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Nam Định năm 2022 - 2023 (Tự luận)
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Hà Nội năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Hồ Chí Minh năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Đà Nẵng năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 tỉnh Vĩnh Phúc năm 2022 - 2023
- Đề thi thử trường THCS & THPT Lương Thế Vinh - Hà Nội 2022-2023
- Đề thi tuyển sinh vào lớp 10 THPT Nghệ An năm 2022-2023
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Huế năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Thanh Hóa năm 2022 - 2023
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Huế năm 2022 - 2023 SVIP
Câu 1. (1,5 điểm)
a) Tìm điều kiện của $x$ để biểu thức $A=\sqrt{x-3}$ có nghĩa.
b) Không sử dụng máy tính cầm tay, tính giá trị của biểu thức $B=\sqrt{2}(\sqrt{8}-\sqrt{3})+\sqrt{6}$.
c) Rút gọn biểu thức $C=\dfrac{x}{\sqrt{x}+x}+\frac{\sqrt{x}-1}{x-1}$ với $x>0$ và $x \neq 1$.
Hướng dẫn giải:
a) $A=\sqrt{x-3}$ có nghĩa khi và chỉ khi $x-3 \geq 0 \Leftrightarrow x \geq 3$.
Vậy với $x \geq 3$ thì biểu thức $A=\sqrt{x-3}$ có nghĩa.
b) $B=\sqrt{2}(\sqrt{8}-\sqrt{3})+\sqrt{6}$
$=\sqrt{2}(2 \sqrt{2}-\sqrt{3})+\sqrt{6}=\sqrt{2}.2 \sqrt{2}-\sqrt{2} \sqrt{3}+\sqrt{6}=4-\sqrt{6}+\sqrt{6}=4$.
Vậy $B=4$
c) Với $x>0$ và $x \neq 1$ ta có $C=\dfrac{x}{\sqrt{x}+x}+\dfrac{\sqrt{x}-1}{x-1}=\dfrac{x}{\sqrt{x}(\sqrt{x}+1)}+\dfrac{\sqrt{x}-1}{(\sqrt{x}+1)(\sqrt{x}-1)}$
$=\dfrac{x}{\sqrt{x}(\sqrt{x}+1)}+\dfrac{1}{\sqrt{x}+1}=\dfrac{x+\sqrt{x}}{\sqrt{x}(\sqrt{x}+1)}=\dfrac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}+1)}=1.$
Vậy $C=1$ với $x>0$ và $x \neq 1$.
Câu 2. (1,5 điểm)
a) Không sử dụng máy tính cầm tay, giải hệ phương trình $\left\{\begin{aligned}&x-2 y=1 \\ &3 x+y=10\\ \end{aligned}\right.$
b) Trên mặt phẳng tọa độ $Oxy$, cho đường thẳng $(d): \, y=2 m x-1$. Tìm $m$ để đường thẳng $(d)$ đi qua điểm $A(1 ; 2)$.
Hướng dẫn giải:
a) $\left\{\begin{aligned} &x - 2y = 1 \\ &3x + y = 10\\ \end{aligned} \Leftrightarrow \left\{\begin{aligned} & x = 1 + 2y \\ &3(1 + 2y) + y = 10\\ \end{aligned} \Leftrightarrow \left\{\begin{aligned} &x = 1 + 2.1 = 3\\ &y = 1\\ \end{aligned} \Leftrightarrow \left\{\begin{aligned} &x=3 \\ &y=1 \end{aligned}\right.\right.\right.\right. $
Vậy hệ phương trình có tập nghiệm $S=\{(3 ; 1)\}$
b) Trên mặt phẳng tọa độ $Oxy$, cho đường thẳng $(d): \, y=2 m x-1$.
Đường thẳng $(d)$ đi qua điểm $A(1 ; 2)$ khi và chỉ khi $2=2 m.1-1 \Leftrightarrow m=\dfrac{3}{2}$.
Vậy với $m=\dfrac{3}{2}$ thì đường thẳng $(d)$ đi qua điểm $A(1 ; 2)$
Câu 3. (1,0 điểm) Hưởng ứng chiến dịch tình nguyện "Mùa hè xanh" để giúp học sinh vùng cao đến trường thuận lợi hơn, hai tổ thanh niên $A$ và $B$ tham gia sửa một đoạn đường. Nếu hai tổ cùng làm thì trong $8$ giờ xong việc. Nếu làm riêng thì thời gian hoàn thành công việc của tổ $A$ ít hơn tổ $B$ là $12$ giờ. Hỏi nếu làm riêng thì mỗi tổ sửa xong đoạn đường đó trong bao lâu?
Hướng dẫn giải:
Gọi $x$ là thời gian (giờ) tổ thanh niên $A$ sửa riêng hoàn thành một đoạn đường $(x>0)$.
Gọi $y$ là thời gian (giờ) tổ thanh niên $B$ sửa riêng hoàn thành một đoạn đường $(y>0)$.
Khi đó, trong một giờ tổ thanh niên $A$ làm riêng sửa được $\dfrac{1}{x}$ đoạn đường và trong một giờ tổ thanh niên $B$ làm riêng sửa được $\dfrac{1}{y}$ đoạn đường.
Vì nếu hai tổ cùng làm thì trong $8$ giờ xong việc nên ta có phương trình $\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{8}$ (1).
Vì nếu làm riêng thì thời gian hoàn thành công việc của tổ $A$ ít hơn tổ $B$ là $12$ giờ nên ta có phương trình $y-x=12$ (2).
Từ (1), (2) ta có hệ phương trình $\left\{\begin{aligned}&\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{8} \\ &y-x=12\\ \end{aligned} \Leftrightarrow\left\{\begin{aligned}&\dfrac{1}{x}+\dfrac{1}{12+x}=\dfrac{1}{8} \\ &y=12+x\\ \end{aligned}\right.\right.$
Giải $\dfrac{1}{x}+\dfrac{1}{12+x}=\dfrac{1}{8}$ ta có: $\dfrac{1}{x}+\dfrac{1}{12+x}=\dfrac{1}{8} \Leftrightarrow \dfrac{8(12+x)}{8 x(12+x)}+\dfrac{8 x}{8 x(12+x)}=\dfrac{x(12+x)}{8 x(12+x)}$
Suy ra $8(12+x)+8 x=x(12+x) \Leftrightarrow x^{2}+4 x+96=0 \Leftrightarrow\left[\begin{aligned}&x=-8 \\ &x=12\\ \end{aligned} \Rightarrow x=12\right.$ vì $(x>0)$.
Ta có $x=12 \Rightarrow y=12+12=24$.
Vậy thời gian tổ thanh niên $A$ sửa riêng hoàn thành một đoạn đường là $12$ giờ và thời gian tổ thanh niên $B$ sửa riêng hoàn thành một đoạn đường là $24$ giờ
Câu 4. (2,0 điểm) Cho phương trình $x^{2}-2(m-1) x+m^{2}-3=0$ (1) (với $x$ là ẩn số)
a) Giải phương trình (1) khi $m=0$.
b) Tìm các giá trị của $m$ để phương trình (1) có nghiệm.
c) Tìm giá trị của $m$ để phương trình (1) có nghiệm $x_{1} ; \, x_{2}$ sao cho biểu thức $F=x_1^2+x_2^{2}+x_{1}+x_{2}$ đạt giá trị nhỏ nhất.
Hướng dẫn giải:
a) Với $m=0$ phương trình $(1)$ trở thành $x^{2}+2 x-3=0$.
Phương trình $x^{2}+2 x-3=0$ có $a+b+c=1+2+(-3)=0$.
Do đó phương trình (1) có nghiệm $\left[\begin{aligned}&x=1 \\ &x=\dfrac{-3}{1}=-3\\ \end{aligned}\right.$.
Vậy phương trình (1) có tập nghiệm $S=\{1 ;-3\}$.
b) Phương trình (1) có $\Delta'=[-(m-1)]^{2}-1 .\left(m^{2}-3\right)=4-2 m$ với mọi giá trị của $m$.
Phương trình (1) có nghiệm khi và chỉ khi $\Delta' \geq 0$ hay $4-2 m \geq 0 \Leftrightarrow m \leq 2$.
Vậy với $m \leq 2$ thì phương trình (1) có nghiệm.
c) Với $m \leq 2$ áp dụng hệ thức Vi-et ta có $\left\{\begin{aligned}&x_{1}+x_{2}=2(m-1) \\ &x_{1} x_{2}=m^{2}-3\\ \end{aligned}\right.$
Ta có $F=x_{1}^{2}+x_{2}^{2}+x_{1}+x_{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}+\left(x_{1}+x_{2}\right)$
$ =[2(m-1)]^{2}-2\left(m^{2}-3\right)+2(m-1)=2 m^{2}-6 m+8=\dfrac{1}{2}(2 m-3)^{2}+\dfrac{7}{2}$
Ta có $F=\dfrac{1}{2}(2 m-3)^{2}+\dfrac{7}{2} \geq \dfrac{7}{2}$ với mọi $m \leq 2$.
Biểu thức $F$ có giá trị nhỏ nhất là $\dfrac{7}{2}$ đạt được khi $(2 m-3)^{2}=0$ hay $2 m-3=0 \Leftrightarrow m=\dfrac{3}{2}$.
Vậy với $m=\dfrac{3}{2}$ thì phương trình (1) có nghiệm $x_{1} ; \, x_{2}$ sao cho biểu thức $F=x_{1}^{2}+x_{2}^{2}+x_{1}+x_{2}$ đạt giá trị nhỏ nhất.
Câu 5. (3,0 điểm) Cho tam giác $A B C$ có ba góc nhọn, $A B<A C$ và nội tiếp đường tròn $(O)$. Gọi $B E$, $C F$ là các đường cao và $H$ là trực tâm của tam giác $A B C$.
a) Chứng minh $A E H F$ là tứ giác nội tiếp.
b) Đường tròn ngoại tiếp tứ giác $A E H F$ cắt đường tròn $(O)$ tại điểm thứ hai $I$, ($A$ không trùng với $I$). Chứng minh hai tam giác $I B C$ và $I F E$ đồng dạng với nhau.
c) Hai đường thẳng $B C$ và $E F$ cắt nhau tại $K$. Chứng minh ba điểm $A, \, I, \, K$ thằng hàng.
Hướng dẫn giải:

a) Chứng minh $AEHF$ là tứ giác nội tiếp.
Trong tam giác $ABC$ có $BE$ và $CF$ là các đường cao cắt nhau tại $H$
$\Rightarrow BE \perp AC$; $CF \perp AB$
$\Rightarrow \widehat{AEB}=\widehat{AFB}=90^{\circ}$ hay $\widehat{AEH}=\widehat{AFH}=90^{\circ}$.
Trong tứ giác $AEHF$ có $\widehat{AEH}+\widehat{AFH}=90^{\circ}+90^{\circ}=180^{\circ}$
$\Rightarrow$ Tứ giác $AEHF$ là tứ giác nội tiếp đường tròn (Tổng hai góc đối trong một tứ giác bằng $180^{\circ}$.
b) Vì $E ; \, F$ cùng nhìn $AH$ dưới một góc vuông $\Rightarrow AEHF$ nội tiếp đường tròn đường kính $AH$.
Gọi tâm đường tròn ngoại tiếp tứ giác $AEHF$ là $O'$, ($O'$ là trung điểm của $AH$).
Ta có $\left(O'\right)$ cắt $(O)$ tại $I$ suy ra $I \in (O)$ và $I' \in \left({O'\right)$
$\Rightarrow AIFE$ nội tiếp đường tròn $\left(O'\right)$
$\Rightarrow \widehat{IAF}=\widehat{IEF}$ (hai góc nội tiếp cùng chắn cung $IF$) (1)
Và $\widehat{IFE}+\widehat{IAE}=180^{\circ}$ (2)
Do $I \in(O)$ và $I' \in\left(O'\right)$ nên $A I B C$ nội tiếp $(O)$
$\Rightarrow \widehat{IAB}=\widehat{ICB}$ (hai góc nội tiếp cùng chắn cung $IB$) (3)
Và $\widehat{IBC}+\widehat{IAC}=180^{\circ}$ (4)
Từ (1) và (3) suy ra $\widehat{I E F}=\widehat{I C B} \, (=\widehat{I A B})$
Từ (2) và (4) $\Rightarrow \widehat{I F E}=\widehat{I B C}$ (cùng bù với $\widehat{I A E}$)
Xét $\triangle I B C$ và $\triangle I F E$ có:
$\widehat{I E F}=\widehat{I C B}$ (cmt)
$\widehat{I F E}=\widehat{I B C}$ (cmt)
Vậy $\triangle I B C \backsim \triangle I F E$ (g.g)
c) Tứ giác $I A E F$ nội tiếp $\Rightarrow \widehat{I F K}=\widehat{I A E}$.
Tứ giác $I A B C$ nội tiếp $\Rightarrow \widehat{I B K}=\widehat{I A E}$.
Suy ra $\widehat{I F K}=\widehat{I B K}$ suy ra tứ giác $I F B K$ nội tiếp.
$\Rightarrow \widehat{K I F}+\widehat{K B F}=180^{\circ}$.
Mà $\widehat{K B F}=\widehat{F E C}=\widehat{F I A}$.
Nên $\widehat{K I F}+\widehat{F I A}=180^{\circ}$.
Vậy ba điểm $A, \, I, \, K$ thằng hàng.
Câu 6. (1,0 điểm) Người ta nhấn chìm hoàn toàn một viên bi sắt đặc vào một cốc thủy tinh chứa nước có dạng hình trụ thì nước trong cốc dâng lên thêm $2$ cm và không tràn ra ngoài cốc (như hình vẽ).
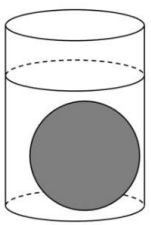
Biết đường kính đáy của cốc bằng $6$ cm (bỏ qua bề dày của thành cốc). Tính thể tích của viên bi.
Hướng dẫn giải:
Bán kính đáy của cốc là $\dfrac{6}{2}=3$ cm.
Vì viên bi sắt đặc được nhấn chìm hoàn toàn trong nước nên thể tích của lượng nước dâng lên chính là thể tích của viên bi và có giá trị:
$V=\pi 3^{2} 2=18 \pi$ cm$^{3}$.
Vậy thể tích của viên bi là $18 \pi$ cm$^{3}$.
