Bài học cùng chủ đề
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Nam Định năm 2022 - 2023 (Trắc nghiệm)
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Nam Định năm 2022 - 2023 (Tự luận)
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Hà Nội năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Hồ Chí Minh năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Đà Nẵng năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 tỉnh Vĩnh Phúc năm 2022 - 2023
- Đề thi thử trường THCS & THPT Lương Thế Vinh - Hà Nội 2022-2023
- Đề thi tuyển sinh vào lớp 10 THPT Nghệ An năm 2022-2023
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Huế năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Thanh Hóa năm 2022 - 2023
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề và đáp án tuyển sinh vào lớp 10 thành phố Hà Nội năm 2022 - 2023 SVIP
Cho hai biểu thức $A=\dfrac{3 \sqrt{x}}{\sqrt{x}+2}$ và $B=\dfrac{x+4}{x-4}-\dfrac{2}{\sqrt{x}-2}$ vói $x \geq 0, x \neq 4$.
1) Tính giá trị của biểu thức $A$ khi $x=9$.
2) Chứng minh $B=\dfrac{\sqrt{x}}{\sqrt{x}+2}$.
3) Tìm số nguyên dương $x$ lớn nhất thỏa mãn $A-B<\dfrac{3}{2}$.
Hướng dẫn giải:
1) Thay $x=9(TMĐK)$ vào biểu thức $A$, ta có: $A=\dfrac{3 \sqrt{9}}{\sqrt{9}+2}=\dfrac{9}{5}$.
2)
$\text { Ta có: } B=\dfrac{x+4}{(\sqrt{x}+2)(\sqrt{x}-2)}-\dfrac{2}{\sqrt{x}-2}=\dfrac{x+4-2(\sqrt{x}+2)}{(\sqrt{x}+2)(\sqrt{x}-2)}$
$=\dfrac{x-2 \sqrt{x}}{(\sqrt{x}+2)(\sqrt{x}-2)}=\dfrac{\sqrt{x}(\sqrt{x}-2)}{(\sqrt{x}+2)(\sqrt{x}-2)}=\dfrac{\sqrt{x}}{\sqrt{x}+2}$
3)
$ A-B=\dfrac{2 \sqrt{x}}{\sqrt{x}+2} \text {. }$
$ \left.A-B<\dfrac{3}{2} \Leftrightarrow \dfrac{2 \sqrt{x}}{\sqrt{x}+2}<\dfrac{3}{2} \Leftrightarrow 4 \sqrt{x}<3 \sqrt{x}+6 \text { (vì } x \geq 0 \Rightarrow \sqrt{x}+2>0\right)$
$ \Leftrightarrow \sqrt{x}<6 \text {, dẫn tới } x<36 $
Kết hợp với điều kiện và yêu cầu của bài toán, suy ra $x=35$.
Vậy số nguyên dương $x$ lớn nhất thỏa mãn $A-B<\dfrac{3}{2}$ là $x=35$.
Giải bài toán sau bằng cách lâp phương trình hoăc hệ phương trình:
Một ô tô và một xe máy cùng khởi hành từ địa điểm $A$ và đi đến địa điểm $B$. Do vận tốc của ô tô lớn hơn vận tốc của xe máy là $20 km / h$ nên ô tô đến $B$ sớm hơn xe máy 30 phút. Biết quãng đường $A B$ dài $60 km$, tính vận tốc của mỗi xe. (Giả định rằng vận tốc mỗi xe là không đổi trên toàn bộ quãng đường $A B$.)
Hướng dẫn giải:
Gọi vận tốc của xe máy khi di chuyên từ $A$ đên $B$ là $x(km / h)$. Điều kiện $x>0$.
Vận tốc của ô tô là $x+20(km / h)$.
Vì quãng đường $A B$ dài $60 km$ nên:
+Thời gian xe máy đi từ $A$ đến $B$ là $\dfrac{60}{x}$ (giờ);
+Thời gian ô tô đi từ $A$ đến $B$ là $\dfrac{60}{x+20}$ (giờ).
Đổi 30 phút $=\dfrac{1}{2}$ (giờ).
Vì ô tô đến B sớm hơn xe máy $\dfrac{1}{2}$ giờ nên ta có phương trình $\dfrac{60}{x}-\dfrac{60}{x+20}=\dfrac{1}{2}$ $\Leftrightarrow x^2+20 x-2400=0$
$\Delta^{\prime}=10^2-1 \cdot(-2400)=2500 \Rightarrow \Delta^{\prime}>0, \sqrt{\Delta^{\prime}}=50$.
Phương trình có hai nghiệm: $x_1=\dfrac{-10+50}{1}=40 ; x_2=\dfrac{-10-50}{1}=-60$.
Đối chiếu điều kiện ta được $x=40$.
Vậy vận tốc xe máy là $40 km / h$ và vận tốc ô tô là $60 km / h$.
Quả bóng đá thường được sử dụng trong các trận thi đấu dành cho trẻ em từ 6 tuổi đến 8 tuổi có dạng một hình cầu với bán kính bằng $9,5 cm$. Tính diện tích bề mặt của quả bóng đó (lấy $\pi \approx 3,14$ ).
Hướng dẫn giải:
Diện tích bề mặt quả bóng hình cầu là: $S=4 \pi R^2 \approx 4.3,14 \cdot(9,5)^2$.
Vậy $S \approx 1133,54\left(cm^2\right)$.
Giải hệ phương trình
$\left\{\begin{array}{l}2 x+\dfrac{12}{y+2}=5 \\3 x-\dfrac{4}{y+2}=2\end{array}\right. \text {. }$
Hướng dẫn giải:
ĐK: $y \neq-2$
$\begin{aligned}& \mathrm{HPT} \Leftrightarrow\left\{\begin{array} { l } { 2 x + \dfrac { 1 2 } { y + 2 } = 5 } \\{ 3 x - \dfrac { 4 } { y + 2 } = 2 }\end{array} \Leftrightarrow \left\{\begin{array} { l } { 2 x + \dfrac { 1 2 } { y + 2 } = 5 } \\{ 9 x - \dfrac { 1 2 } { y + 2 } = 6 }\end{array} \Leftrightarrow \left\{\begin{array}{l}11 x=11 \\2 x+\dfrac{12}{y+2}=5\end{array}\right.\right.\right. \\& \Leftrightarrow\left\{\begin{array} { l } { x = 1 } \\{ \dfrac { 1 2 } { y + 2 } = 3 }\end{array} \Leftrightarrow \left\{\begin{array}{l} x=1 \\y=2\end{array}\right.\right.\end{aligned}$
Đối chiếu điều kiện, ta được hệ phương trình có nghiệm là $(x ; y)=(1 ; 2)$.
Trong mặt phẳng toạ độ $O x y$, cho parabol $(P): y=x^2$ và đường thẳng $(d): y=2 x+m^2$.
a) Chứng minh $(d)$ luôn cắt $(P)$ tại hai điểm phân biệt.
b) Tìm tất cả giá trị của $m$ để $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1, x_2$ thỏa mãn $\left(x_1+1\right)\left(x_2+1\right)=-3$.
Hướng dẫn giải:
Xét phương trình hoành độ giao điểm của đường thằng $(d)$ và parabol $(P)$ : $x^2=2 x+m^2 \Leftrightarrow x^2-2 x-m^2=0$ (1)
Ta có: $\Delta^{\prime}=1+m^2$. Suy ra $\Delta^{\prime}>0$ với mọi giá trị của $m$.
Do đó phương trình (1) luôn có 2 nghiệm phân biệt.
Vậy $(d)$ luôn cắt $(P)$ tại hai điểm phân biệt.
Vì $x_1, x_2$ là hoành độ giao điểm của của đường thẳng $(d)$ và parabol $(P)$ nên $x_1, x_2$ là hai nghiệm của phương trình (1).
Theo định lý Vi-ét, ta có: $\left\{\begin{array}{l}x_1+x_2=2 \\ x_1 \cdot x_2=-m^2\end{array}\right.$.
Từ đó: $\left(x_1+1\right)\left(x_2+1\right)=-3 \Leftrightarrow x_1+x_2+x_1 \cdot x_2+4=0$.
Suy ra $2-m^2+4=0 \Leftrightarrow m= \pm \sqrt{6}$.
Vậy đề $\left(x_1+1\right)\left(x_2+1\right)=-3$ thì $m= \pm \sqrt{6}$.
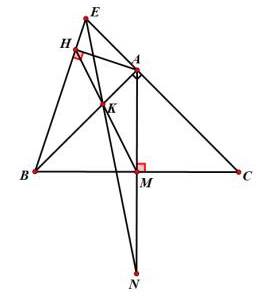
Cho tam giác $A B C$ vuông cân tại định $A$. Gọi $E$ là một điểm bất kỳ trên tia $C A$ sao cho điềm $A$ nằm giữa hai điểm $C$ và $E$. Gọi $M$ và $H$ lần lượt là chân các đường vuông góc kẻ từ điểm $A$ đến các đường thẳng $B C$ và $B E$.
1) Chứng minh tứ giác $A M B H$ là tứ giác nội tiếp.
2) Chứng minh $B C \cdot B M=B H$. $B E$ và $H M$ là tia phân giác của góc $A H B$.
3) Lấy điểm $N$ sao cho $M$ là trung điềm của đoạn thẳng $A N$. Gọi $K$ là giao điểm của hai đường thẳng $E N$ và $A B$. Chứng minh ba điểm $H, K, M$ là ba điểm thẳng hàng.
Hướng dẫn giải:
1) $\mathrm{Vi} A M \perp B C \Rightarrow \widehat{A M B}=90^{\circ}$
Vi $A H \perp B E \Rightarrow \widehat{A H B}=90^{\circ}$.
Xét tứ giác $A M B H$ có:
$\widehat{A M B}+\widehat{A H B}=90^{\circ}+90^{\circ}=180^{\circ}$.
Mà hai góc này ờ vị trí đối nhau nên tứ giác $A M B H$ là tứ giác nội tiếp.
2) Xét tam giác $A B C$ vuông tại $A$, có đường cao $A M$ nên $A B^2=B M \cdot B C$ (1) (hệ thức lượng trong tam giác vuông).
Xét tam giác $A B E$ vuông tại $A$, có đường cao $A H$ nên $A B^2=B H \cdot B E$ (2) (hệ thức lượng trong tam giác vuông).
Từ (1), (2) $\Rightarrow B C \cdot B M=B H \cdot B E$.
Ta có: $\widehat{A H M}=\widehat{A B M}$ (3) (hai góc nội tiếp cùng chắn cung $A M$ của đường tròn ngoại tiếp tứ giác $A M B H$ ).
Ta có: $\widehat{B H M}=\widehat{B A M}$ (4) (hai góc nội tiếp cùng chắn cung $B M$ của đường tròn ngoại tiếp tứ giác $A M B H$ ).
Vì tam giác $A M B$ cân tại $M \Rightarrow \widehat{A H M}=\widehat{B H M}$ (5)
Vì tia $H M$ nằm giữa hai tia $H A, H B$ nên từ $(3),(4)$, (5) suy ra tia $H M$ là tia phân giác của $\widehat{A H B}$.
3) Vì tam giác $A B C$ vuông cân tại $A$ và $A M \perp B C$ nên $M$ là trung điểm $B C$. Tứ giác $A C N B$ có hai đường chéo $A N$ và $B C$ cắt nhau tại trung điểm $M$ của mỗi đường chéo nên tứ giác $A C N B$ là hình bình hành.
Hình bình hành $A C N B$ có hai đường chéo $A N$ và $B C$ vuông góc nhau nên tứ giác $A C N B$ là hình thoi. Do đó $N B=A B$ và $N B / / A E$.
Áp dụng định lý Talet trong tam giác $A K E$ ta có: $\dfrac{K A}{K B}=\dfrac{A E}{B N}=\dfrac{A E}{A B}(6)$
Mặt khác, $\dfrac{A E}{A B}=\dfrac{A H}{H B}(=\tan \widehat{A B E})(7)$.
Từ $(6),(7)$ suy ra: $\dfrac{K A}{K B}=\dfrac{A H}{H B}$, do đó tia $H K$ là tia phân giác của $\widehat{A H B}(8)$. Mà tia $H M$ là tia phân giác của $\widehat{A H B}(9)$.
Từ $(8),(9)$ suy ra ba điểm $H, K, M$ thẳng hàng.
Hướng dẫn giải:
Vì $x, y \geq 0$ nên $P \geq 0$ và $P^2=x^2+4 x y+4 y^2=\left(x^2+y^2\right)+\left(4 x y+3 y^2\right) \geq 4$.
Từ đó $P^2 \geq 4 \Leftrightarrow P \geq 2$.
Với $x=2, y=0$ (thỏa mãn điều kiện bài toán), ta có: $P=2$.
Vậy giá trị nhỏ nhất của $P$ bằng 2 .
