Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Nam Định năm 2022 - 2023 (Tự luận) SVIP

Hướng dẫn giải:

a) Chứng minh $\dfrac{8 \sqrt{2}-\sqrt{32}-4}{1-\sqrt{2}}=-4$

Ta có: VT $= \dfrac{8 \sqrt{2}-\sqrt{32}-4}{1-\sqrt{2}}$

$=\dfrac{8 \sqrt{2}-\sqrt{2 . 4^2}-4}{1-\sqrt{2}} =\dfrac{8 \sqrt{2}-4 \sqrt{2}-4}{1-\sqrt{2}}$

$=\dfrac{4 \sqrt{2}-4}{1-\sqrt{2}} =\dfrac{-4(1-\sqrt{2})}{1-\sqrt{2}} =-4=$ V P

Vậy $\dfrac{8 \sqrt{2}-\sqrt{32}-4}{1-\sqrt{2}}=-4$

b) ĐKXĐ: $\left\{\begin{aligned}x \geq 0 \\ \sqrt{x}+2 \neq 0 \\ \sqrt{x}-2 \neq 0 \\ x-4 \neq 0\end{aligned}\right.\Leftrightarrow\left\{\begin{aligned}x \geq 0 \\ \sqrt{x} \neq 2 \\ x \neq 4\end{aligned} \Leftrightarrow\left\{\begin{aligned}x \geq 0 \\ x \neq 4\end{aligned}\right.\right.$.

Vậy ĐKXĐ của ${P}$ là $x \geq 0$, $x \neq 4$.

Với $x \geq 0$, $x \neq 4$ ta có:

$P =\left(\dfrac{2}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}-2}+\dfrac{7}{x-4}\right) .(\sqrt{x}-1) $

$=\left(\dfrac{2}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}-2}+\dfrac{7}{(\sqrt{x}-2)(\sqrt{x}+2)}\right) .(\sqrt{x}-1)$

$=\left(\dfrac{2(\sqrt{x}-2)-(\sqrt{x}+2)+7}{(\sqrt{x}-2)(\sqrt{x}+2)}\right) .(\sqrt{x}-1)$

$=\dfrac{2 \sqrt{x}-4-\sqrt{x}-2+7}{(\sqrt{x}-2)(\sqrt{x}+2)} .(\sqrt{x}-1) $

$=\dfrac{\sqrt{x}+1}{(\sqrt{x}-2)(\sqrt{x}+2)} .(\sqrt{x}-1) $

$=\dfrac{x-1}{x-4}$.

Vậy $P=\dfrac{x-1}{x-4}$ với $x \geq 0$, $x \neq 4$.

Hướng dẫn giải:

a) Ta có: $\Delta =(-m)^2-4(m-5) =m^2-4 m+20 =m^2-4 m+4+16 =(m-2)^2+16>0$ $\forall m$.

Do đó phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị $m$.

b) Gọi $x_1$, $x_2$ là hai nghiệm của phurơng trình (1).

Theo hệ thức Vi-ét ta có: $\left\{\begin{aligned}x_1+x_2=\dfrac{-b}{a}=m \\ x_1 x_2=m-5\end{aligned}\right.$

Ta có: $x_1+2 x_2=1 \Leftrightarrow x_1=1-2 x_2$

Thay $x_1=1-2 x_2$ vào $x_1+x_2=m$ ta có: $1-2 x_2+x_2=m \Leftrightarrow-x_2=m-1 \Leftrightarrow x_2=1-m$.

Suy ra $x_1=1-2(1-m)=1-2+2 m=2 m-1$

Thay $x_1$; $x_2$ vào $x_1 x_2=m-5$ ta có: $ (2 m-1)(1-m)=m-5$

$\Leftrightarrow -2 m^2+2 m-1+m-m+5=0$

$\Leftrightarrow -2 m^2+2 m+4=0 \Leftrightarrow m^2-m-2=0$.

Phương trình có $a-b+c=1-(-1)+(-2)=0$ nên có mọ̉t nghiệm $m=-1$, nghiệm còn lại $m=-\dfrac{c}{a}=2$.

Vậy $m \in\{-1 ; 2\}$ là các giá trị thỏa mãn yêu cầu.

Hướng dẫn giải:

Ta có $\left\{\begin{aligned} &2 x - y - 2 = 0\\ &3 x^2 - x y - 8 = 0\\ \end{aligned} \Leftrightarrow \left\{\begin{aligned} &y=2 x-2 \\ &3 x^2-x(2 x-2)-8=0\\ \end{aligned}\right.\right.$

$\Leftrightarrow \left\{\begin{aligned} &y = 2 x - 2 \\ &3 x^2 - 2 x^2 + 2 x - 8 = 0\\ \end{aligned} \Leftrightarrow \left\{\begin{aligned} &y=2 x-2 \\ &x^2+2 x-8=0 \, \,  (*)\\ \end{aligned}\right.\right.$.

Phương trình $\left(^*\right)$ có $\Delta'=1+8=9>0$ nên phương trình có hai nghiệm phân biệt $\left[\begin{aligned}&x_1=-1+3=2 \\ &x_2=-1-3=-4\\ \end{aligned}\right.$

+ Với $x_1=2 \Rightarrow y_1=2 x_1-2=2.2-2=2$.

+ Với $x_2=-4 \Rightarrow y_2=2 x_2-2=2 .(-4)-2=-10$.

Vậy hệ phương trinh có nghiệm $(x ; y)$ là $(2 ; 2)$ và $(-4 ;-10)$.

Hướng dẫn giải:

1) Diện tích tam giác $ABC$ là: $S_1=\dfrac{1}{2} A B . A C=\dfrac{1}{2} . 4 . 4=8$ (cm$^2$).

Áp dụng định lí Py-ta-go trong tam giác vuông $ABC$ ta có:

$B C^2=A B^2+A C^2 \Rightarrow B C^2=4^2+4^2 \Rightarrow B C^2=32 \Rightarrow B C=4 \sqrt{2}$ (cm).

Mà $AH$ là đường cao của tam giác cân $ABC$ đồng thời là đường trung tuyến ứng với cạnh huyền $BC$

$ \Rightarrow A H=\dfrac{1}{2} B C=\dfrac{1}{2} . 4 \sqrt{2}=2 \sqrt{2}$ (cm)

Diện tích hình quạt $ADE$ bằng $\dfrac14$ diện tích hình tròn tâm ${A}$, bán kính ${AH}$ nên có diện tích là $S_2=\dfrac{1}{4} \pi . A H^2=\dfrac{1}{4} \pi .(2 \sqrt{2})^2=2 \pi$ (cm$^2$).

Vậy diện tích phần tô màu là $S=S_1-S_2=8-2 \pi$ (cm$^2$). 

2)

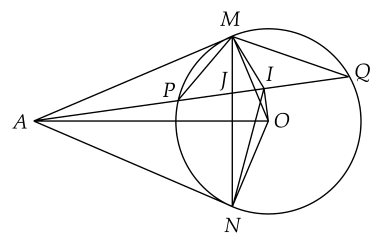
a) Năm điểm $A, \, M, \, O, \, I, \, N$ cùng nằm trên một đường tròn và $\widehat{ J IM}=\widehat{ J I N}$.

Xét đường tròn $(O)$ có $I$ là trung điểm của dây cung $PQ$ (dây cung $PQ$ không đi qua tâm $O$)

$\Rightarrow O I \perp P Q$ (quan hệ đường kính và dây cung)

$\Rightarrow \widehat{PIO}=90^{\circ} \Rightarrow \widehat{ A I O}=90^{\circ}$

$\Rightarrow \triangle A I O$ vuông tại $I \Rightarrow I$ thuộc đường tròn đường kính ${AO}$.

$AM$ là tiếp tuyến của đường tròn $(O) \Rightarrow \widehat{ A M O}=90^{\circ}$ (tính chất tiếp tuyến của đường tròn)

$\Rightarrow \triangle A M O$ vuông tại $M$ $\Rightarrow M$ thuộc đường tròn đường kính ${AO}$.

$A N$ là tiếp tuyến cua đường tròn $(O) \Rightarrow \widehat{ A N O}=90^{\circ}$ (tính chất tiếp tuyến của đường tròn)

$\Rightarrow N$ thuộc đường tròn đường kính ${AO}$.

Ta có $I, \, M, \, N$ cùng thuộc đường tròn đường kính ${AO}$

$\Rightarrow$ Năm điểm ${A}, \, {M}, \, {O}, \, {I}, \, {N}$ cùng nằm trên một đường tròn (đpcm).

$\widehat{ JI M}=\widehat{ J I N}$ 

${AM}$, $AN$ là tiếp tuyến của đường tròn $(O) \Rightarrow OA$ là phân giác của $\widehat{ M O N}$ (tính chất hai tiếp tuyến cắt nhau)

$ \Rightarrow \widehat{ A O M}=\widehat{ A O N}$.

Ta có $\widehat{ A O M}=\widehat{ A IM}$ (hai góc nội tiếp cùng chắn cung $AM$)

$\widehat{ A O N}=\widehat{ A I N}$ (hai góc nội tiếp cùng chắn cung $AN$)

Mà $\widehat{ A O M}=\widehat{ A O N}$ (cmt) 

$\Rightarrow \widehat{ A I M}=\widehat{ A I N}$

$\Rightarrow \widehat{J IM}=\widehat{ J I N}$ (đpcm)

b) Tam giác $AMP$ đồng dạng với tam giác $A Q M$ và $A P . A Q=A I . A J$.

Xét $(O)$ có: $\widehat{ M Q P}=\widehat{ A M P}$ (góc nội tiếp; góc tạo bởi tiếp tuyến và dây cung cùng chắn cung $PM$)

$\Rightarrow \widehat{MQA} = \widehat{AMP}$

Xét $\triangle A M P$ và $\triangle A Q M$ có:

$\widehat{ M A Q}$ chung;

$\widehat{ A M P}=\widehat{ M Q A}$ (cmt)

$\Rightarrow \triangle A M P \backsim \triangle A Q M$ (g.g)

$\Rightarrow \dfrac{A P}{A M}=\dfrac{A M}{A Q}$ (cặp cạnh tương ứng tỉ lệ)

$\Rightarrow A P . A Q=A M^2$

Ta có: $\widehat{ A M N}=\widehat{ A I N}$ (hai góc nội tiếp cùng chắn cung $AN$)

$\Rightarrow \widehat{ A M J}=\widehat{ J I N}$

Mà $\widehat{ J IM}=\widehat{ J I N}$ (cmt)

$\Rightarrow \widehat{ A M J}=\widehat{ J IM}$

$\Rightarrow \widehat{ A M J}=\widehat{ A I M} $

Xét $\triangle A M J$ và $\triangle A I M$ có:

$\widehat{ M A I}$ chung

$\widehat{ A M J}=\widehat{ A I M}$ (cmt)

$\Rightarrow \triangle A M J \backsim \triangle A I M$ (g.g)

$\Rightarrow \dfrac{A M}{A I}=\dfrac{A J}{A M}$ (cặp cạnh tương ứng tỉ lệ)

$\Rightarrow A I . A J=A M^2$

Từ (1) và (2) $\Rightarrow A P . A Q=A I . A J$.

Hướng dẫn giải:

a) Giải phương trinh: $x+4=\sqrt{x^2+9 x+19}-2 \sqrt{x+3}$

ĐKXĐ: $x \geq-3$.

$x+4=\sqrt{x^2+9 x+19}-2 \sqrt{x+3} \Leftrightarrow x+3+2 \sqrt{x+3}+1=\sqrt{x^2+6 x+9+3 x+10} $

$\Leftrightarrow (\sqrt{x+3}+1)^2=\sqrt{(x+3)^2+3(x+3)+1}$.

Đặt $x+3=t, \, (t \geq 0)$, khi đó phương trình trở thành: $(\sqrt{t}+1)^2=\sqrt{t^2+3 t+1}$

Vì $(\sqrt{t}+1)^2>0$, nên ta có: $\left[(\sqrt{t}+1)^2\right]^2=t^2+3 t+1$

$\Leftrightarrow(t+2 \sqrt{t}+1)^2=t^2+3 t+1$

$\Leftrightarrow t^2+4 t+1+4 t \sqrt{t}+2 t+4 \sqrt{t}=t^2+3 t+1 $

$\Leftrightarrow t^2+4 t+1+4 t \sqrt{t}+2 t+4 \sqrt{t}-t^2-3 t-1=0 $

$\Leftrightarrow 4 t \sqrt{t}+3 t+4 \sqrt{t}=0 $

$\Leftrightarrow \sqrt{t}(4 t+3 \sqrt{t}+4)=0$

$\Leftrightarrow \left\{ \begin{aligned}&\sqrt{t}=0 \\ &4 t+3 \sqrt{t}+4=0\\ \end{aligned} \right.$

Vì $t \geq 0 \Rightarrow 4 t+3 \sqrt{t} \geq 0 \Rightarrow 4 t+3 \sqrt{t}+4>0 \Rightarrow 4 t+3 \sqrt{t}+4=0$ vô nghiệm.

Suy ra $\sqrt{l}=0 \Rightarrow l=0$ (thỏa mãn).

Với $t=0 \Rightarrow \sqrt{x+3}=0  \Leftrightarrow x+3=0  \Leftrightarrow x=-3$ (thỏa mãn)

Vậy phương trình có nghiệm duy nhất là $x=-3$.

b) Ta xét $A=(x+y-z)(y+z-x)(z+x-y)$

Nhận thấy: $x+y-z+y+z-x+z+x-y=x+y+z \geq 0$.

TH1: $A$ có $2$ thừa số dương, $1$ thừa số âm.

Khi đó $A<0 \Rightarrow A-x y z<0$ (vì $x, \, y, \, z>0$)

Nên GTLN của $P < 0$.

TH2: $A$ có $2$ thừa số âm, $1$ thừa số dương (điều này vô lí) vì tổng của $2$ thừa số bất kì luôn $\geq 0$

TH3: $A$ có $3$ thừa số đều không âm.

Sử dụng bất đẳng thức Cauchy ta có:

$(x+y-z)(y+z-x) \leq\left(\dfrac{x+y-z+y+z-x}{2}\right)^2=y^2 $

$(y+z-x)(z+x-y) \leq\left(\dfrac{y+z-x+z+x-y}{2}\right)^2=z^2 $

$(z+x-y)(x+y-z) \leq\left(\dfrac{z+x-y+x+y-z}{2}\right)^2=x^2 $

Nhân vế với vế của ba bất đẳng thức trên ta được: ${[(x+y-z)(y+z-x)(z+x-y)]^2 \leq x^2 y^2 z^2} $

$\Leftrightarrow(x+y-z)(y+z-x)(z+x-y) \leq x y z $

$\Leftrightarrow(x+y-z)(y+z-x)(z+x-y)-x y z \leq 0$

Dấu bằng xảy ra khi $x=y=z$.

Vậy GTLN của $P=0$ khi $x=y=z$.