Đề số 2 (thời gian: 90 phút) SVIP

Hướng dẫn giải:

a) $2x+4=x-1 \Leftrightarrow 2x-x=-1-4 \Leftrightarrow x=-5$.

Vậy tập nghiệm của phương trình đã cho là \(S = \left\{ { - 5} \right\}\).

b) 

\(\begin{aligned} & 2 x(x-3)-5(x-3)=0 \\ \Leftrightarrow & (2 x-5)(x-3)=0 \\ \Leftrightarrow & {\left[\begin{array}{l} 2 x-5=0 \\ x-3=0 \end{array}\right.} \\ \Leftrightarrow & {\left[\begin{array}{l} \displaystyle x=\frac{5}{2} \\ x=3. \end{array}\right.} \end{aligned}\)

Vậy tập nghiệm của phương trình đã cho là $\displaystyle S = \left\{ {\frac{5}{2};3} \right\}$.

c) 

\(\begin{aligned} & \frac{2 x}{x+1}=\frac{x^2-x+8}{(x+1)(x-4)} \text{(đk: } x \neq -1, x\neq 4 \text{)}\\ \Leftrightarrow & \frac{2 x(x-4)}{(x+1)(x-4)}=\frac{x^2-x+8}{(x+1)(x-4)} \\ \Rightarrow & 2 x(x-4)=x^2-x+8 \\ \Leftrightarrow & 2 x^2-8 x-x^2+x-8=0 \\ \Leftrightarrow & x^2-7 x-8=0 \\ \Leftrightarrow & x^2-8 x+x-8=0 \\ \Leftrightarrow & (x+1)(x-8)=0 \\ \Leftrightarrow & {\left[\begin{array}{l} x=-1 \text{(loại)} \\ x=8\text{(tm)} \end{array}\right.} \end{aligned}\)

Vậy tập nghiệm của phương trình đã cho là $S = \left\{ 8 \right\}$.

Hướng dẫn giải:

Gọi độ dài quãng đường $AB$ là $x$ $(\mathrm{km})$, $x>0$. 

Thời gian người đó đi từ $A$ đến $B$ là $\displaystyle \frac{x}{15}$ (giờ).

Thời gian người đó đi từ $B$ về $A$ là $\displaystyle \frac{x}{12}$ (giờ).

Vì thời gian về nhiều hơn thời gian đi là \(22\) phút \(=\dfrac{11}{30}\) giờ nên ta có phương trình:

\(\displaystyle \frac{x}{12}-\frac{x}{15}=\frac{11}{30} \Leftrightarrow 15 x-12 x=\frac{11}{30}.12.15 \Leftrightarrow x=22\) (thỏa mãn). 

Vậy độ dài quãng đường $AB$ là $22 \mathrm{~km}$.

Hướng dẫn giải:

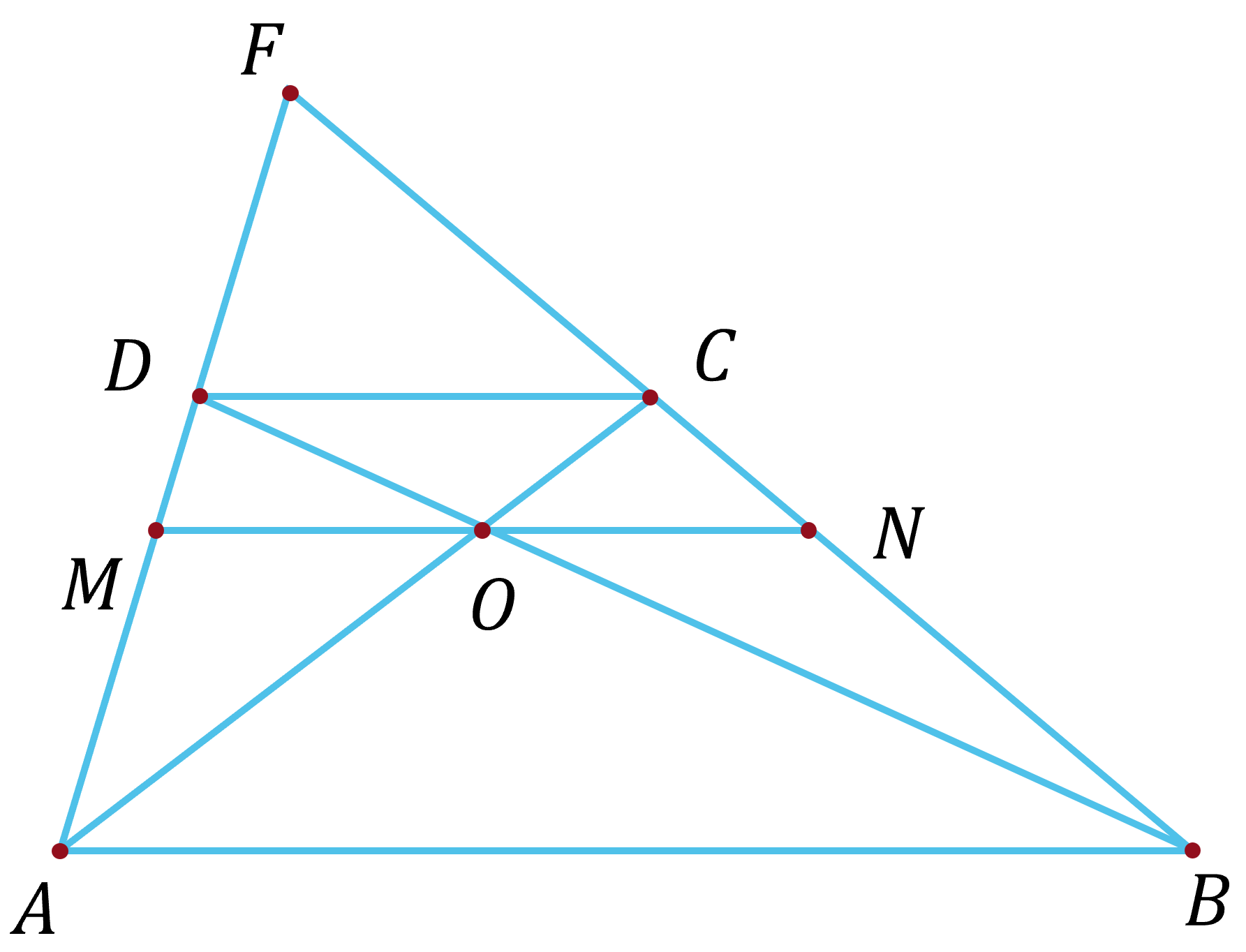
a) Xét tam giác $OAB$ có $CD \parallel AB$: 

$\displaystyle \frac{OC}{OA}= \frac{OD}{OB} = \frac{CD}{AB}$ (định lí Thales)

hay $\displaystyle \frac{OC}{12}= \frac{3}{9} = \frac{CD}{18}$

suy ra $OC=4cm, CD=6cm$. 

b) Xét tam giác $FAB$ có $CD \parallel AB$: 

$\displaystyle \frac{FD}{DA} = \frac{FC}{CB}$ (định lí Thales)

suy ra $FD.BC=FC.AD$.

c) Xét tam giác $DAB$ có $MO \parallel AB$: 

$\displaystyle \frac{OM}{AB} = \frac{DO}{OB} = \frac{1}{3}$ (định lí Thales).

Xét tam giác $CAB$ có $NO \parallel AB$: 

$\displaystyle \frac{ON}{AB} = \frac{CO}{OA} = \frac{1}{3}$ (định lí Thales).

Suy ra $\displaystyle \frac{OM}{AB} = \frac{ON}{AB}$ 

do đó $OM=ON$. 

Hướng dẫn giải:

Ta có: 

\(\begin{aligned} & \left(x^2+1\right)^2+3 x\left(x^2+1\right)+2 x^2=0 \\ \Leftrightarrow & \left(x^2+1\right)^2+x\left(x^2+1\right)+2 x\left(x^2+1\right)+2 x^2=0 \\ \Leftrightarrow & \left(x^2+1\right)\left(x^2+x+1\right)+2 x\left(x^2+x+1\right)=0 \\ \Leftrightarrow & \left(x^2+1+x\right)(x+1)^2=0 \\ \Leftrightarrow & (x+1)^2=0\left(x^2+1+x = {\left( {x + \frac{1}{2}} \right)^2} + \frac{3}{4}> 0, \forall x \in \mathbb{R}\right) \\ \Leftrightarrow & x=-1 \end{aligned}\)

Vậy tập nghiệm của phương trình đã cho là $S = \left\{ { - 1} \right\}$.