Đề số 1 (thời gian: 90 phút) SVIP

Hướng dẫn giải:

a) \(\displaystyle\frac{x-3}{5}+\frac{1+2 x}{3}=6 \Leftrightarrow 3 x-9+5+10 x=90 \Leftrightarrow 13 x=94 \Leftrightarrow x=\frac{94}{13}\).

Vậy tập nghiệm của phương trình đã cho là \(S=\left\{\dfrac{94}{13}\right\}\).

b) \(\left(2x-3\right)\left(x^2+1\right)=0\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x^2+1=0\end{matrix}\right.\Leftrightarrow2x-3=0\Leftrightarrow x=\dfrac{3}{2}\).

Vậy tập nghiệm của phương trình đã cho là \(S=\left\{\dfrac{3}{2}\right\}\).

c)

 \(\begin{aligned} & \frac{2}{x+1}-\frac{1}{x-2}=\frac{3 x-11}{(x+1)(x-2)} \text{(đk: } x \neq -1, x \neq 2 \text{)}\\ \Rightarrow & 2(x-2)-(x+1)=3 x-11 \\ \Leftrightarrow & 2 x-4-x-1=3 x-11 \\ \Leftrightarrow & -2 x=-6 \\ \Leftrightarrow & x=3 (\text{thỏa mãn}) \end{aligned}\)

Vậy tập nghiệm của phương trình đã cho là \(S=\left\{3\right\}\).

Hướng dẫn giải:

Gọi $x$ là chữ số hàng chục của số cần tìm ($x \in \mathbb{N}^*, 0 < x \le 9$).

Vì số cần tìm là số lẻ và chia hết cho $5$ nên chữ số hàng đơn vị của số đó là $5$. 

Vì hiệu của số đó và chữ số hàng chục của nó bằng $86$ nên ta có phương trình: 

\(\overline {x5} - x = 86 \Leftrightarrow \left( {10x + 5} \right) - x = 86\)

\( \Leftrightarrow 9x = 81 \Leftrightarrow x = 9\) (thỏa mãn).

Vậy số cần tìm là $95$. 

Hướng dẫn giải:

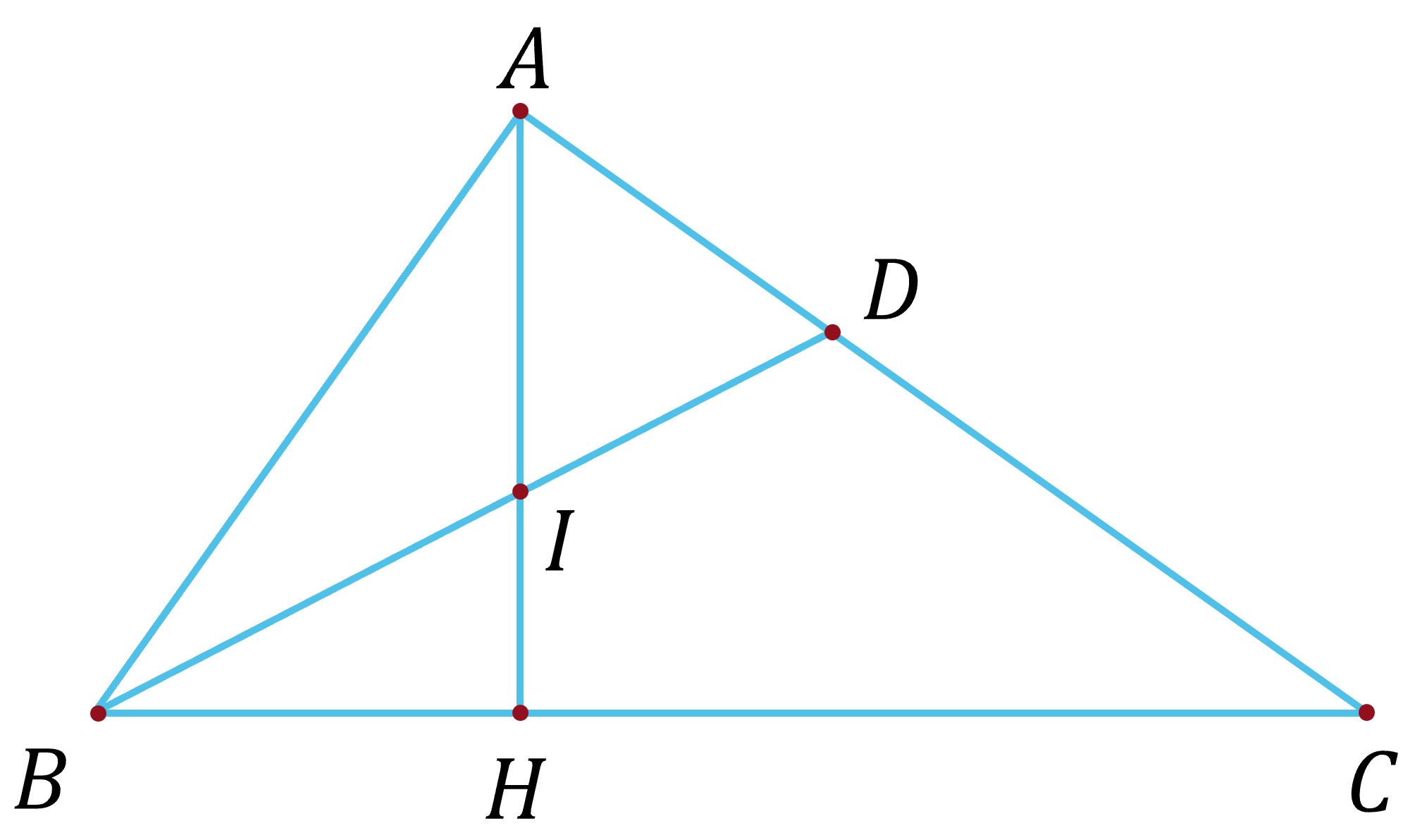
a) Xét tam giác $ABC$ vuông tại $A$: 

$BC^2=AB^2+AC^2$ (định lí Pythagoras)

$\Leftrightarrow BC^2 = 6^2+8^2=100 \Leftrightarrow BC = 10 (cm)$. 

Xét tam giác $ABC$ phân giác $BD$ có: 

$\displaystyle\frac{AB}{BC} = \frac{AD}{DC} \Leftrightarrow \frac{AB}{BC+AB} = \frac{AD}{DC+AD}$ 

$\displaystyle\frac{AD}{AC} = \frac{AB}{BC+AB} \Leftrightarrow AD = 3(cm)$

suy ra $DC=5(cm)$.

b) Xét tam giác $ABH$ phân giác $BI$ có: $\displaystyle\frac{IH}{IA} = \frac{HB}{AB}$.

Xét $\triangle HBA$ và $\triangle ABC$ có: 

$\widehat{HBA} = \widehat{ABC}$ (góc chung)

$\widehat{BHA} = \widehat{BAC} (=90^\circ)$

suy ra $\triangle HBA \sim \triangle ABC$ (g.g).

Suy ra $\displaystyle\frac{HB}{AB} = \frac{BA}{BC}$ 

$\displaystyle\Rightarrow \frac{BA}{BC} = \frac{IH}{IA}$. 

Mà ta lại có $\displaystyle\frac{AB}{BC} = \frac{AD}{DC}$ nên $\displaystyle\frac{IH}{IA} = \frac{AD}{DC}$. 

c) Ta có $\triangle ABD \sim \triangle HBI$ (g.g) 

suy ra $\displaystyle \frac{AB}{HB} = \frac{BD}{BI} \Rightarrow AB.BI = BD.HB$.

$\widehat{BDA} = \widehat{BIH}$ (hai góc tương ứng) 

mà $\widehat {BIH} = \widehat{AID}$ (hai góc đối đỉnh)

suy ra $\widehat{BDA} = \widehat{AID}$ 

do đó tam giác $AID$ cân tại $A$.

Hướng dẫn giải:

Ta có: 

\(\begin{aligned} & x^2-4 x+y^2-6 y+15=2 \\ \Leftrightarrow & x^2-4 x+4+y^2-6 y+9=0 \\ \Leftrightarrow & (x-2)^2+(y-3)^2=0 \\ \Leftrightarrow & \left\{ \begin{array}{l} {\left( {x - 2} \right)^2} = 0\\ {\left( {y - 3} \right)^2} = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 2\\ y = 3 \end{array} \right. \\ \end{aligned}\)

(vì $(x-2)^2 \ge 0$ với mọi $x \in \mathbb{R}$, $(y-3)^2 \ge 0$ với mọi $y \in \mathbb{R}$).

Vậy $x=2$, $y=3$.