Đề số 3 (thời gian: 90 phút) SVIP

Hướng dẫn giải:

a) Điều kiện: \(x\ne\pm1,x\ne-4\).

\(A=\left(\dfrac{2}{x+1}-\dfrac{1}{x-1}\right)\div\dfrac{x+4}{x^2-1}\)

\(=\left[\dfrac{2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}-\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}\right].\dfrac{x^2-1}{x+4}\)

\(=\dfrac{2x-2-x-1}{\left(x+1\right)\left(x-1\right)}.\dfrac{\left(x+1\right)\left(x-1\right)}{x+4}=\dfrac{x-3}{x+4}\).

Vậy \(A=\dfrac{x-3}{x+4}\) với \(x\ne\pm1,x\ne-4\).

b) \(A=\dfrac{x-3}{x+4}=\dfrac{x+4-7}{x+4}=1-\dfrac{7}{x+4}\) (\(x\ne\pm1,x\ne-4\))

Để \(A\) nguyên thì \(\dfrac{7}{x+4}\) nguyên mà \(x\) nguyên nên \(x+4\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)

\(\Leftrightarrow x\in\left\{-11;-5;-3;3\right\}\) (thỏa mãn).

Hướng dẫn giải:

a) \(x-5=7-x\Leftrightarrow x+x=7+5\Leftrightarrow2x=12\Leftrightarrow x=6\).

Vậy tập nghiệm của phương trình đã cho là \(S=\left\{6\right\}\).

b) \(3x-15=2x\left(x-5\right)\)

\(\Leftrightarrow3\left(x-5\right)-2x\left(x-5\right)=0\)

\(\Leftrightarrow\left(3-2x\right)\left(x-5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}3-2x=0\\x-5=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=5.\end{matrix}\right.\)

Vậy tập nghiệm của phương trình đã cho là \(S=\left\{\dfrac{3}{2};5\right\}\).

c) 

\(\begin{aligned} & \frac{1}{x^2+5 x+6}+\frac{1}{x^2+7 x+12}+\frac{1}{x^2+9 x+20}+\frac{1}{x^2+11 x+30}=\frac{1}{8} \\ & \Leftrightarrow \frac{1}{(x+2)(x+3)}+\frac{1}{(x+3)(x+4)}+\frac{1}{(x+4)(x+5)}+\frac{1}{(x+5)(x+6)}=\frac{1}{8} \end{aligned}\)

Điều kiện xác định: \(x\notin\left\{-6;-5;-4;-3;-2\right\}\). Phương trình đã cho tương đương với

\(\begin{aligned} & \frac{1}{x+2}-\frac{1}{x+3}+\frac{1}{x+3}-\frac{1}{x+4}+\frac{1}{x+4}-\frac{1}{x+5}+\frac{1}{x+5}-\frac{1}{x+6}=\frac{1}{8} \\ & \Leftrightarrow \frac{1}{x+2}-\frac{1}{x+6}=\frac{1}{8} \Rightarrow 8(x+6)-8(x+2)=(x+2)(x+6) \\ & \Leftrightarrow x^2+8 x-20=0 \Leftrightarrow(x-2)(x+10)=0 \\ & \Leftrightarrow\left[\begin{array} { l l } { x - 2 = 0 } \\ { x + 1 0 = 0 } \end{array} \Leftrightarrow \left[\begin{array}{ll} x=2 & (\text { tm }) \\ x=-10 & (\text { tm }) \end{array}\right.\right. \end{aligned}\)

Vậy tập nghiệm của phương trình đã cho là \(S=\left\{2;-10\right\}\).

Hướng dẫn giải:

Gọi độ dài quãng đường $AB$ là $x (\mathrm{km}), x>0$.

Vận tốc lúc đi của người đó là $\displaystyle\frac{x}{3} (\mathrm{km} / \mathrm{h})$.

Vận tốc lúc đi của người đó là $\displaystyle\frac{x}{4} (\mathrm{km} / \mathrm{h})$.

Vì lúc đi từ $B$ về $A$ người đó đi với vận tốc bé hơn vận tốc lúc đi là $10 \mathrm{~km} / \mathrm{h}$ nên ta có phương trình:

$\displaystyle\frac{x}{3}-\frac{x}{4} = 10 \Leftrightarrow \frac{4x-3x}{12}=10 \Leftrightarrow x=120 (\text{tm})$.

Vậy độ dài quãng đường $AB$ là $120 \mathrm{~km}$; vận tốc ô tô khi đi từ $A$ đến $B$ là $\displaystyle\frac{120}{3}=40~(\mathrm{km}/\mathrm{h})$. 

Hướng dẫn giải:

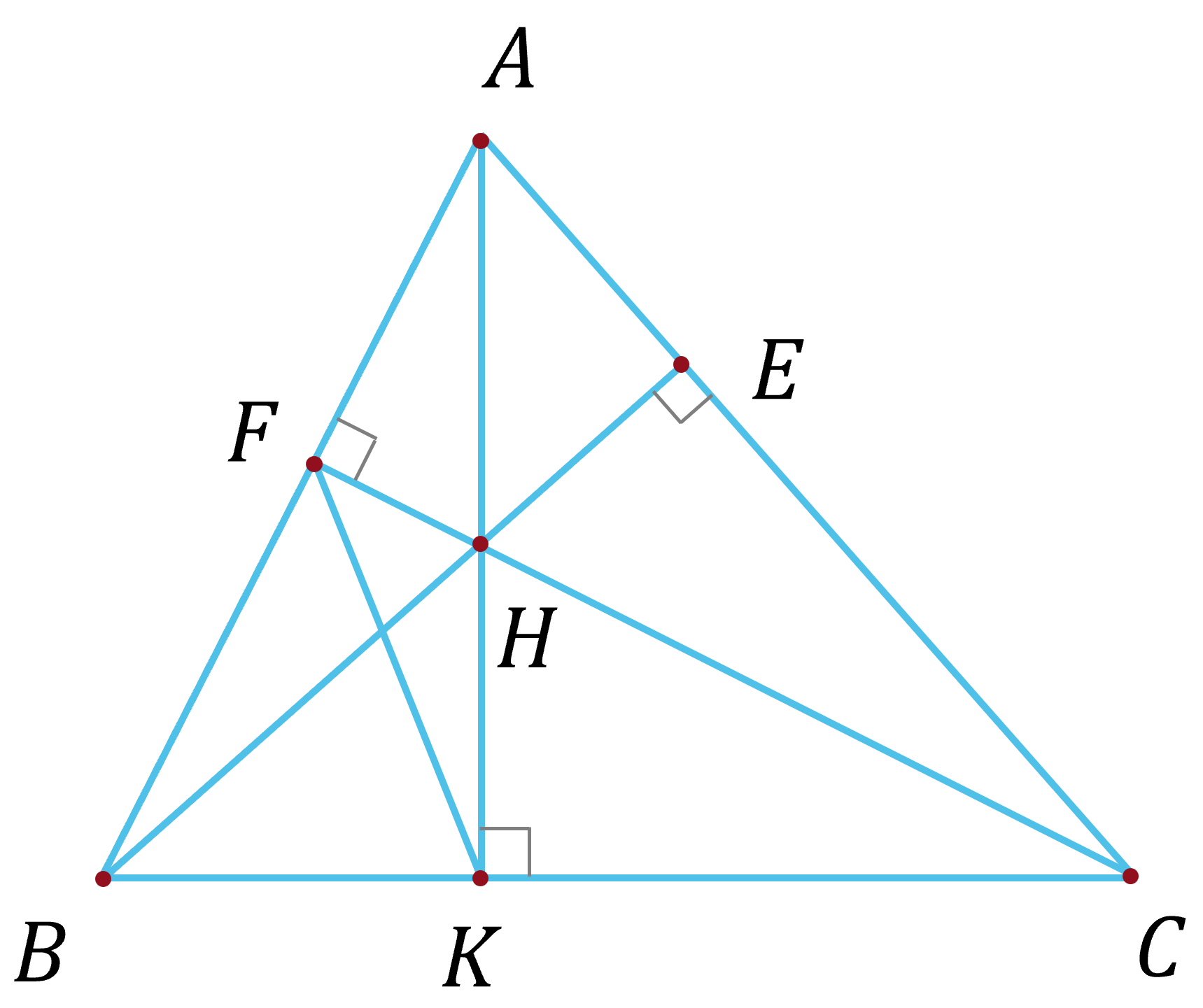
a) Vì đường cao $BE$, $CF$ của tam giác $ABC$ cắt nhau tại $H$ nên $H$ là trực tâm của $\triangle ABC$. Suy ra $AH \bot BC$ tại $K$.

Do $AK \bot BC$ suy ra $\widehat{AKB}=90^\circ$, $CF \bot AB$ suy ra $\widehat{CFB}=90^\circ$.

Xét $\triangle BAK$ và $\triangle BCF$ có: 

$\widehat{ABK}=\widehat{CBF}$ (góc chung)

$\widehat{AKB} = \widehat{CFB} (=90^\circ)$

suy ra $\triangle BAK \backsim \triangle BCF$ (g.g)

 \(\displaystyle\Rightarrow \frac{B A}{B C}=\frac{B K}{B F} \Rightarrow B A \cdot B F=B K \cdot B C\) (1).

b) Xét $\triangle BKF$ và $\triangle BAC$ có:

$\widehat{KBF} = \widehat{ABC}$ (góc chung)

$\displaystyle\Rightarrow \frac{B A}{B C}=\frac{B K}{B F}$

suy ra $\triangle BKF \backsim \triangle BAC$ (c.g.c).

c) Chứng minh tương tự ý a), ta thu được $\triangle CAB \backsim \triangle CKE$ 

\(\displaystyle\Rightarrow \frac{CA}{CK}=\frac{CB}{CE} \Rightarrow CA \cdot CE=CB \cdot CK\) (2)

Cộng (1) và (2) vế với vế ta được:

\(B A \cdot B F+C E \cdot C A=B K \cdot B C+C K \cdot B C=B C(B K+C K)=B C^2=16\).