Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 4 (thời gian: 90 phút) SVIP
(2,0 điểm) Giải phương trình:
a) $3x+9=0$;
b) \(\left(x-4\right)\left(x+3\right)=0\);
c) \(5\left(x-2\right)=x+\left(3x-4\right)\).
Hướng dẫn giải:
a) \(3x+9=0\Leftrightarrow3x=-9\Leftrightarrow x=-3\).
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{-3\right\}\).
b) \(\left(x-4\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{4;-3\right\}\).
c) \(5\left(x-2\right)=x+\left(3x-4\right)\)
\(\Leftrightarrow5x-10=x+3x-4\)
\(\Leftrightarrow5x-x-3x=-4+10\)
\(\Leftrightarrow x=6\)
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{6\right\}\).
(2,0 điểm) Cho phương trình \(\dfrac{3}{x+1}+\dfrac{5}{x}=0\).
a) Tìm ĐKXĐ của phương trình trên.
b) Giải phương trình trên.
Hướng dẫn giải:
a) Điều kiện xác định của phương trình đã cho là:
\(\left\{{}\begin{matrix}x+1\ne0\\x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\x\ne0\end{matrix}\right.\)
Vậy điều kiện xác định của phương trình đã cho là \(x\ne-1,x\ne0\).
b) \(\dfrac{3}{x+1}+\dfrac{5}{x}=0\Leftrightarrow\dfrac{3x}{\left(x+1\right).x}+\dfrac{5\left(x+1\right)}{x\left(x+1\right)}=0\)
\(\Rightarrow3x+5\left(x+1\right)=0\)
\(\Leftrightarrow8x+5=0\)
\(\Leftrightarrow x=-\dfrac{5}{8}\) (thỏa mãn)
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{-\dfrac{5}{8}\right\}\).
(1,5 điểm) Giải bài toán sau bằng cách lập phương trình
Một ô tô chạy từ Phan Rang lên Đà Lạt với vận tốc trung bình \(40 \mathrm{~km} / \mathrm{h}\). Sau đó ô tô trở về Phan Rang, ô tô chạy với vận tốc trung bình $60 \mathrm{~km} / \mathrm{h}$. Biết cả đi lẫn về hết $5$ giờ. Tính độ dài quãng đường từ Phan Rang lên Đà Lạt.
Hướng dẫn giải:
Gọi độ dài quãng đường từ Phan Rang lên Đà Lạt là $x$ ($\mathrm{km}$), $x>0$.
Thời gian ô tô đi từ Phan Rang lên Đà Lạt là \(\dfrac{x}{40}\) giờ.
Thời gian ô tô đi từ Đà Lạt về Phan Rang là \(\dfrac{x}{60}\) giờ.
Vì cả đi lẫn về hết $5$ giờ nên ta có phương trình
\(\dfrac{x}{40}+\dfrac{x}{60}=5\Leftrightarrow60x+40x=5.40.60\Leftrightarrow x=120\) (thỏa mãn)
Vậy độ dài quãng đường từ Phan Rang lên Đà Lạt là $120 \mathrm{~km}$.
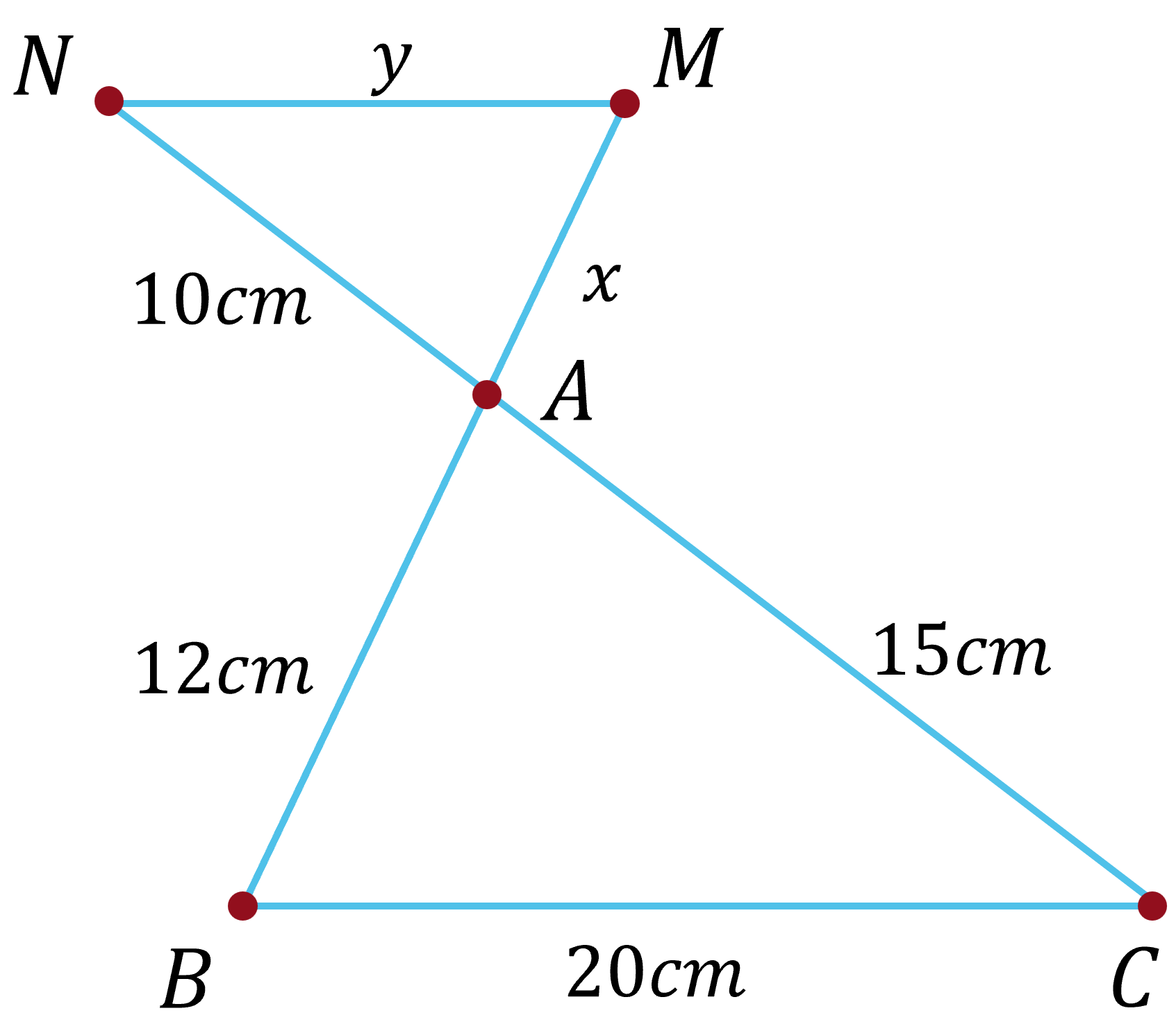
(1,5 điểm) Cho hình vẽ, biết $MN \parallel BC$. Tìm $x$, $y$.
Hướng dẫn giải:
Vì $MN \parallel BC$ nên \(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\) suy ra \(\dfrac{x}{12}=\dfrac{10}{15}=\dfrac{y}{20}\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=\dfrac{40}{3}.\end{matrix}\right.\)
(3,0 điểm) Cho tam giác $ABC$ có $AB=9 \mathrm{~cm}$, $AC=12 \mathrm{~cm}$. Lấy điểm $D$ thuộc $AB$, điểm $E$ thuộc $AC$ sao cho $AD = 3 \mathrm{~cm}$, $AE=4\mathrm{~cm}$.
a) Chứng minh: $\triangle ABC \backsim \triangle ADE$.
b) Chứng minh: $DE \parallel BC$.
c) Cho $BE$ là tia phân giác của góc $\widehat{ABC}$. Tính $BC$.
d) Tính $DE$.
Hướng dẫn giải:
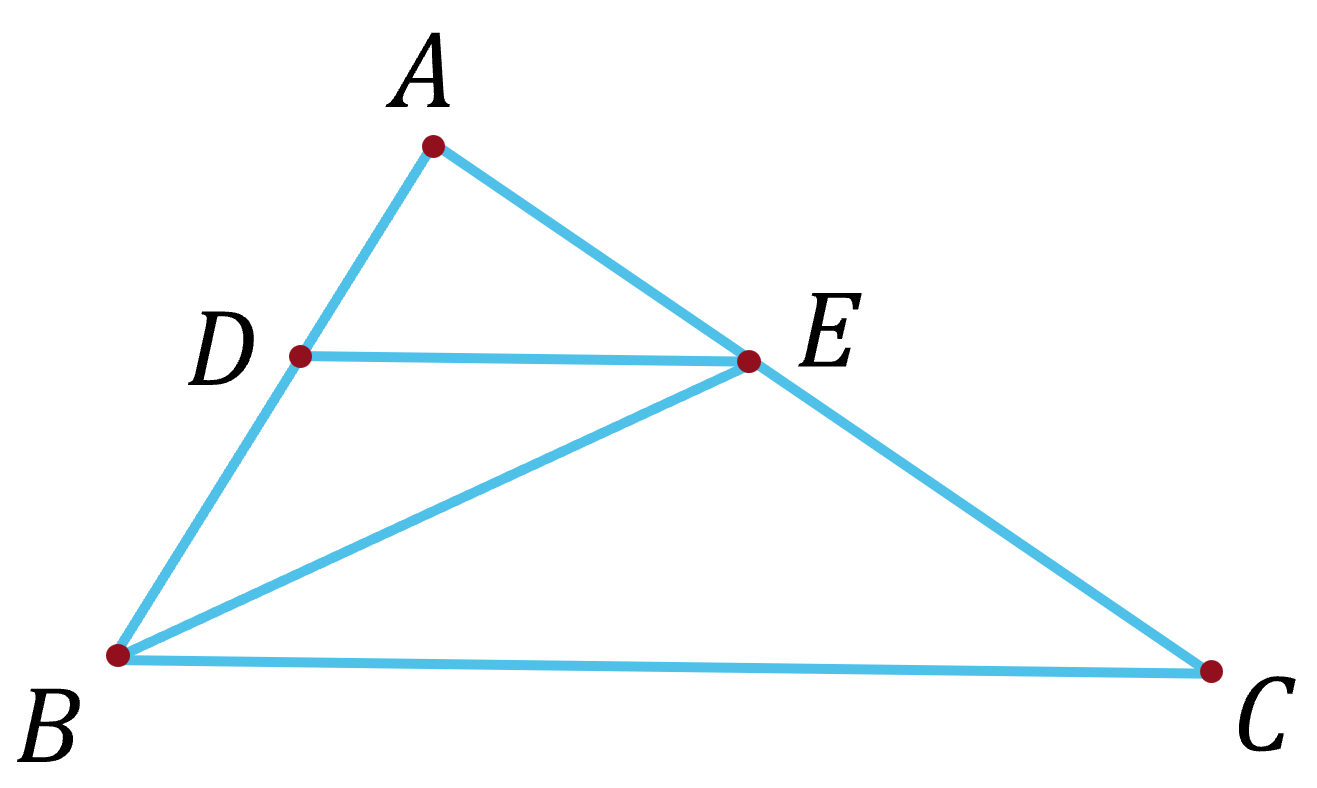
a) Chứng minh: $\triangle ABC \backsim \triangle ADE$
Xét tam giác $ABC$ và tam giác $ADE$ có:
\(\dfrac{AB}{AD}=\dfrac{AC}{AE}\)
$\widehat{BAC} = \widehat{DAE}$ (góc chung)
suy ra $\triangle ABC \backsim \triangle ADE$ (c.g.c).
b) Chứng minh: $DE \parallel BC$
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) suy ra $DE \parallel BC$ (định lí đảo Thales)
c) Tính $BC$
Tam giác $ABC$ có $BE$ là tia phân giác của $\widehat{ABC}$ suy ra
\(\dfrac{AE}{EC}=\dfrac{AB}{BC}\Leftrightarrow\dfrac{4}{8}=\dfrac{9}{BC}\Leftrightarrow BC=18\)$\mathrm{(cm)}$.
d) Tính $DE$
Vì $DE \parallel BC$ nên \(\dfrac{DE}{BC}=\dfrac{AD}{AB}\) hay \(\dfrac{DE}{18}=\dfrac{3}{9}\Leftrightarrow DE=6\)$\mathrm{(cm)}$.
