Chứng minh các điểm cùng thuộc một đường tròn SVIP

Hướng dẫn giải:

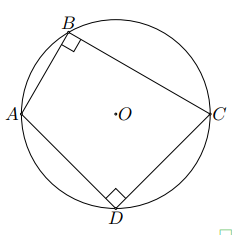
Tứ giác $ABCD$ có $\widehat{B}=\widehat{D}=90^\circ $ nên $OA=OB=OC=OD$ (đường cao ứng với cạnh huyền).

Suy ra bốn điểm $A$, $B$, $C$, $D$ cùng nằm trên một đường tròn tâm $O$, đường kính $AC$.

Hướng dẫn giải:

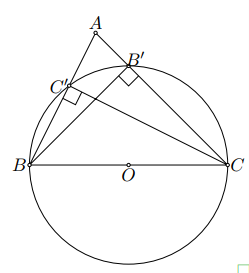
Tam giác $ABC$ có hai đường cao $B{B}'$ và $C{C}'$ nên $\widehat{B{C}'C}=\widehat{B{B}'C}=90^\circ.$

Suy ra $OB=OC=O{B}'=O{C}'$ (đường cao ứng với cạnh huyền).

Do đó bốn điểm $B$, ${C}'$, ${B}'$, $C$ cùng nằm trên một đường tròn.

Hướng dẫn giải:

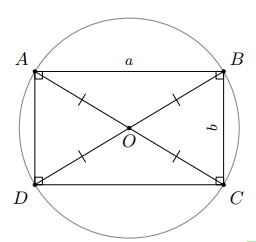
Gọi $O$ là giao điểm của hai đường chéo $AC$ và $BD$.

Theo tính chất hai đường chéo của hình chữ nhật, ta có $OA=OB=OC=OD \, \Big( =\dfrac{1}{2}AC=\dfrac{1}{2}BD \Big)$.

Vậy bốn điểm $A$, $B$, $C$, $D$ cùng thuộc $\Big( O;\dfrac{1}{2}AC \Big)$.

Áp dụng định lí Pythagore vào tam giác vuông $ABC$, ta có: $AC^2=AB^2+BC^2=a^2+b^2$

Do đó $R=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{a^2+b^2}$.

Hướng dẫn giải:

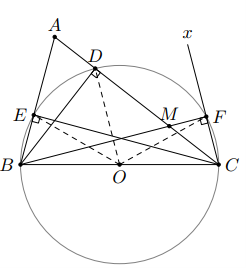
Gọi $O$ là trung điểm của $BC$.

Ta có $BD$ là đường cao nên $BD\bot AC$, hay tam giác $BCD$ vuông tại $D$.

Trong tam giác vuông $BCD$ có $DO$ là trung tuyến ứng với cạnh huyền $BC$ nên:

$OD=OB=OC=\dfrac{1}{2}BC$ $(1)$

Tương tự ta có: $OE=OB=OC=\dfrac{1}{2}BC$ $(2)$

Và $OF=OB=OC=\dfrac{1}{2}BC$ $(3)$

Từ $(1)$, $(2)$ và $(3)$ suy ra $OB=OC=OD=OD=OE=OF$.

Do đó năm điểm $B$, $C$, $D$, $E$, $F$ cùng thuộc một đường tròn.

Hướng dẫn giải:

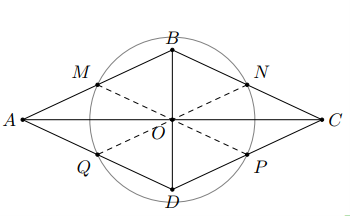
Gọi $M$, $N$, $P$, $Q$ lần lượt là trung điểm của bốn cạnh $AB$, $BC$, $CD$ và $DA$ của hình thoi $ABCD$.

Gọi $O$ là giao điểm của $AC$ và $BD$.

Ta có $AC\bot BD$.

Theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông, ta được:

$OM=\dfrac{1}{2}AB$; $ON=\dfrac{1}{2}BC$;

$OP=\dfrac{1}{2}CD$; $OQ=\dfrac{1}{2}AD$

Mặt khác $AB=BC=CD=DA$ nên $OM=ON=OP=OQ$.

Do đó bốn điểm $M$, $N$, $P$, $Q$ cùng nằm trên một đường tròn.

Hướng dẫn giải:

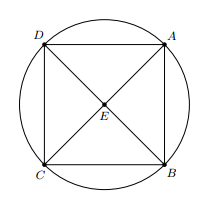
a) Vì hình vuông $ABCD$ có tâm $E$ suy ra $EA=EB=EC=ED$.

Do đó, các điểm $A$, $B$, $C$ và $D$ cùng thuộc một đường tròn tâm $E$.

Hai trục đối xứng của đường tròn là $AC$ và $BD$.

b) Cạnh hình vuông bằng $3$ cm nên áp dụng định lí Pythagore, ta có:

$AC=\sqrt{AB^2+BC^2}=3\sqrt{2}$ suy ra $EA=\dfrac{AC}{2}=\dfrac{3\sqrt{2}}{2}$.

Vậy bán kính của đường tròn là $R=EA=\dfrac{3\sqrt{2}}{2}$ cm.

Hướng dẫn giải:

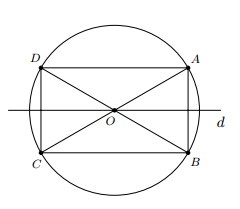
a) Giả sử đường tròn $(O)$ có bán kính $R$ suy ra $OA=R$ $(1)$

Do $B$ là điểm đối xứng với $A$ qua $d$ suy ra $OA=OB$ $(2)$

Do $C$ là điểm đối xứng với $A$ qua $O$ suy ra $OA=OC$ $(3)$

Do $D$ là điểm đối xứng với $B$ qua $O$ suy ra $OB=OD$ $(4)$

Từ $(1)$, $(2)$, $(3)$ và $(4)$ suy ra $B$, $C$ và $D$ cùng thuộc $(O)$.

b) Ta thấy $AC$ và $BD$ cắt nhau tại $O$ là trung điểm của mỗi đường, suy ra $ABCD$ là hình chữ nhật.

c) Ta thấy $OC=OD$ suy ra $d$ là đường trung trực của $CD$.

Suy ra $C$ và $D$ đối xứng với nhau qua $d$.

Hướng dẫn giải:

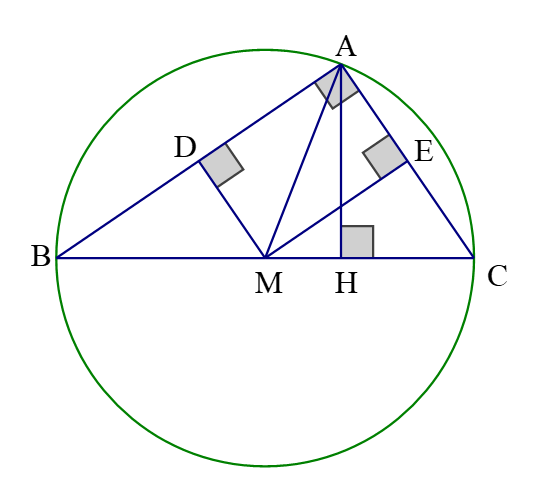
Vì ba tam giác $ADM, \, AEM, \, AHM$ có chung cạnh huyền $AM$ nên ba đỉnh góc vuông $D, \, E, \, H$ nằm trên đường tròn đường kính $AM$ có tâm là trung điểm của $AM$.

Vậy năm điểm $A, \, D, \, M, \, H, \, E$ cùng nằm trên một đường tròn.

Hướng dẫn giải:

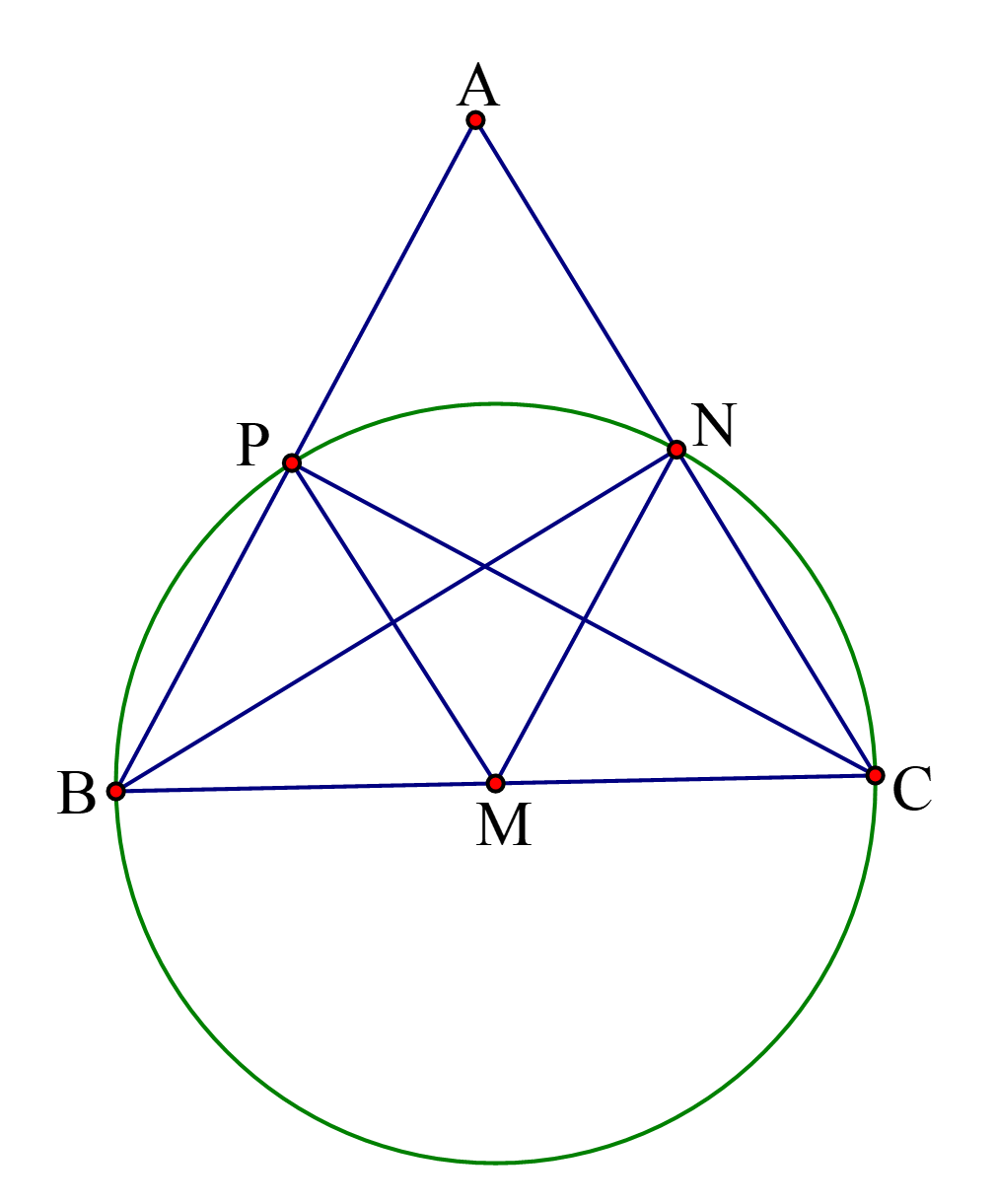
Vì tam giác $ABC$ đều nên các trung tuyến đồng thời cũng là đường cao.

Suy ra $AM, \, BN, \, CP$ lần lượt vuông góc với $BC, \, AC, \, AB$.

$\Delta BPC$ là tam giác vuông, có $BC$ là cạnh huyền nên $MP=\dfrac{1}{2}BC=BM=MC$ (1)

$\Delta BNC$ là tam giác vuông, có $BC$ là cạnh huyền nên $NM=\dfrac{1}{2}BC=BM=MC$ (2) 

Từ (1) và (2) suy ra $PM=NM=MB=MC$ hay các điểm $B, \, P, \, N, \, C$ cùng thuộc đường tròn, đường kính $BC=a$, tâm đường tròn là trung điểm $M$ của $BC$.

Hướng dẫn giải:

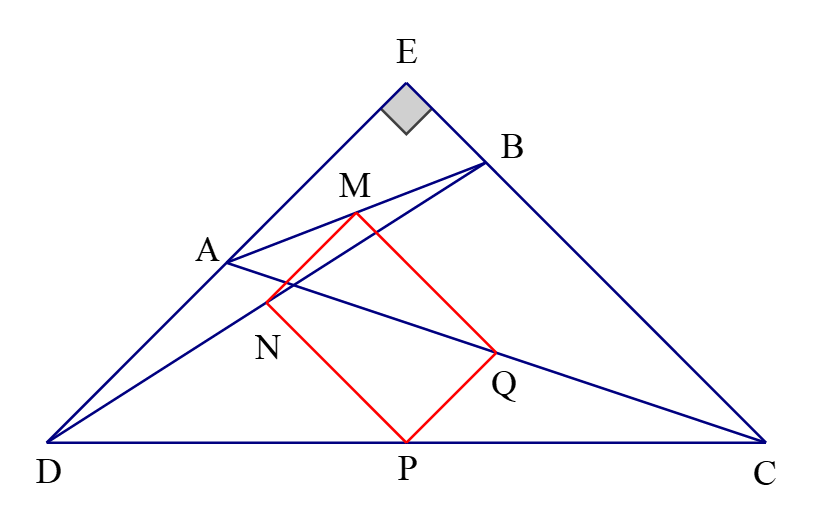
Xét tứ giác $MNPQ$, ta có: $MQ$ // $NP$ và $MN$ // $PQ $ suy ra $MNPQ$ là hình bình hành.

Kéo dài $AD$ và $BC$ cắt nhau tại $E$.

Ta có: $\widehat{C}+\widehat{D}= 90^\circ$ suy ra $\widehat E=90^\circ$.

Lại có:$MN$ // $ED$ và $MQ$ // $EC$ suy ra $MN \bot MQ$

Do đó $MNPQ$ là hình chữ nhật suy ra $M, \, N, \, P, \, Q$ nằm trên một đường tròn với tâm là giao điểm của hai đường chéo của hình chữ nhật, bán kính bằng nửa đường chéo.