bài 1:cho nửa đường tròn (o) đường kính AB và đường thẳng d vuông góc với AB tại H, M là điểm di động trên nửa đường tròn. đường thẳng MA,MB lần lượt tại C và D.
a,c/m HA.HB=HC.HD
b,gọi B' là điểm đói xứng với B qua h .c/m ACDB nội tiếp
c,khi M di đọng trên (o) thì tâm I của đường tròn ngoại tiếp tam giác ABC chạy trên đường nào.
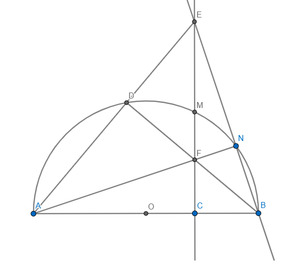
Bài 2:cho (o) và C nằm ngoài đường tròn . kẻ các tiếp tuyến CE , CF với đường tròn , cát tuyến CMN, đường thẳng CO cắt đường tròn tại 2 điểm A và B,CA nằm giữa C và O . gọi I là giao điểm của ABEF
a,c/m tam giácCME đòng dạng tam giác CEN
b,c/m \(CE^2\)= CI .CD
c,c/m tam giác CMI đồng dạng tam giác CON
d,c/m MION nội tiếp
e,c/m góc AIM =góc BIN
__________________________________CÁC BẠN LÀM NHANH HỘ MÌNH NHA ____________________________________________