cho tam giác ABC vuông tại A .Kẻ AH vuông góc BC tại H.Biết BH=18cm,HC=32cm.Tính AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 12 2021
a: Xét ΔABC có \(AC^2=AB^2+BC^2\)
nên ΔABC vuông tại B
BK
Cho tam giác ABC,góc A=90*,AH vuông góc với BC biết HC=18cm,HB=32cm.Tính AH và các cạnh tam giác ABC
1
14 tháng 8 2021
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=18\cdot32=576\)
hay AH=24cm
Ta có: BH+CH=BC
nên BC=18+32=50cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=32\cdot50=1600\\AC^2=18\cdot50=900\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=40cm\\AC=30cm\end{matrix}\right.\)
I
25 tháng 2 2020
a) áp dụng đ/l pitago zô tam giác zuông abh ta đc
=> AB^2=AH^2+HB^2
=> AH^2=Ab^2-HB^2
=> AH=24
áp dụng dl pitago zô tam giác zuông ahc
=> AC^2=AH^2+HC^2
=> AC=40
b) Tco : CH+HB=32+18=50
Tam giac ABC có
\(\hept{\begin{cases}AB^2+AC^2=40^2+30^2=2500\\BC^2=50^2=2500\end{cases}}\)
=> \(AB^2+AC^2=BC^2\)
=> tam giác abc zuông
VT
1
30 tháng 1 2020
https://olm.vn/hoi-dap/tim-kiem?id=1153717&subject=1&q=++++++++++cho+tam+gi%C3%A1c+ABC+vu%C3%B4ng+t%E1%BA%A1i+A+.K%E1%BA%BB+AH+vu%C3%B4ng+g%C3%B3c+BC+t%E1%BA%A1i+H.Bi%E1%BA%BFt+BH=18cm,HC=32cm.T%C3%ADnh+AC+++++++++
3 tháng 3 2022
Ta có: BC = HB+HC = 9+16=25cm
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=\sqrt{225}=15cm\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=AH^2+BH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=\sqrt{144}=12cm\)
3 tháng 3 2022
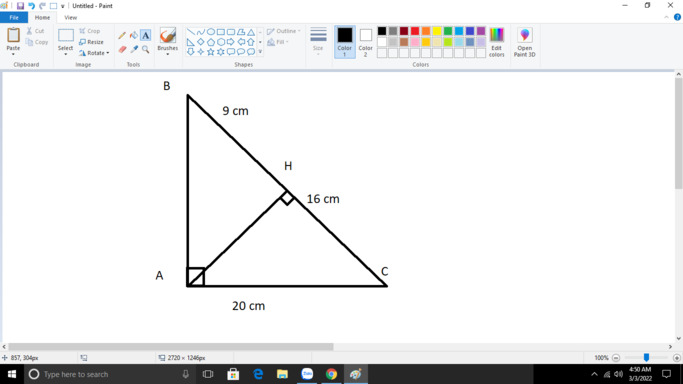
\(BC=BH+HC\)
\(\Rightarrow BC=9cm+16cm=25\left(cm\right)\)
\(\text{Xét }\Delta ABC\text{ vuông tại }A\text{ có:}\)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow AB^2=25^2-20^2=625-400=225\left(cm\right)\)
\(\Rightarrow AB=\sqrt{225}=15\left(cm\right)\)
\(\text{Xét }\Delta AHC\text{ vuông tại }H\text{ có:}\)
\(AC^2=AH^2+HC^2\)
\(\Rightarrow AH^2-AC^2-HC^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow AH^2=20^2-16^2=400-256=144\left(cm\right)\)
\(\Rightarrow AH=\sqrt{144}=12\left(cm\right)\)
PT
3
KT
11 tháng 2 2018
Ap dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
T
14 tháng 2 2018
Ta có hình vẽ:
Áp dụng định lý Pitago. Ta có:
BC2 = AB2 + AC2 <=> 62 + 82 = 100 cm2
100 = 10 x 10
=> BC = 10 cm
Áp dụng công thức Heron để tính chiều cao. Ta có:
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (p là chu vi, S là diện tích, a,b,c là độ dài 3 cạnh)
Ta có: Chu vi tam giác là: 6 + 8 + 10 =24 cm
Vậy \(S=\sqrt{24\left(24-6\right)\left(24-8\right)\left(24-10\right)}=48\sqrt{42}\)
Để tính chiều cao AH, ta lấy 2 lần diện tích chia cho đáy ( BC) sẽ có được chiều cao
2 lần diện tích là: \(48\sqrt{42}.2=96\sqrt{42}\)
\(\Rightarrow AH=96\sqrt{42}:10=\frac{24\sqrt{42}}{25}\)
Độ dài cạnh BH là: (Bạn tự làm)
Độ dài cạnh HC là: (Bạn tự làm nhé)
DT
2
5 tháng 1 2022
BC=25cm
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
=>AC=20cm
PT
9 tháng 2 2021
a) Xét tam giác BAH và tam giác CAH, có:
AH: cạnh chung
AB = AC ( tam giác ABC cân tại A )
góc AHB = góc AHC ( = 90 độ )
-> tam giác BAH = tam giác CAH ( ch-cgv )
-> HB = HC ( 2 cạnh tương ứng )
b) Xét tam giác FBH và tam giác ECH, có:
HB = HC ( cmt )
góc D = góc E ( = 90 độ )
góc B = góc C ( tam giác ABC cân tại A )
-> tam giác FBH = tam giác ECH ( ch-gn )
-> HF = HE ( 2 cạnh tương ứng )
-> tam giác HEF là tam giác cân tại H
9 tháng 2 2021
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
b) Xét ΔFHB vuông tại F và ΔEHC vuông tại E có
BH=CH(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔFHB=ΔEHC(cạnh huyền-góc nhọn)
Suy ra: HF=HE(Hai cạnh tương ứng)
Xét ΔHEF có HF=HE(cmt)
nên ΔHEF cân tại H(Định nghĩa tam giác cân)
Vẽ hình :
Áp dụng định lý Py-ta-go vào \(\Delta ABH\)ta có :
\(AB^2=AH^2+BH^2=AH^2+18^2=AH^2+324\)
\(\Rightarrow\)\(AH^2=AB^2-324\)
Áp dụng định lý Py-ta-go vào \(\Delta AHC\)ta có :
\(AC^2=HC^2+AH^2=32^2+\left(AB^2-324\right)=1024-324+AB^2=700+AB^2\)
\(\Rightarrow\)\(AC=\sqrt{700+AB^2}\)