x4-13x2+36=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 5 2022
3: \(x^4-13x^2+36\)
\(=x^4-9x^2-4x^2+36\)
\(=\left(x^2-9\right)\left(x^2-4\right)\)
\(=\left(x-3\right)\left(x+3\right)\left(x-2\right)\left(x+2\right)\)
4: \(x^4+3x^2-2x+3\)
\(=x^4+x^3+3x^2-x^3-x^2-3x+x^2+x+3\)
\(=\left(x^2+x+3\right)\left(x^2-x+1\right)\)
5: \(x^4+2x^3+3x^2+2x+1\)
\(=x^4+x^3+x^2+x^3+x^2+x+x^2+x+1\)
\(=\left(x^2+x+1\right)^2\)
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
a.
$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$
b.
$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$
c.
$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$
d.
$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$
$=(x+1)(x^2-4x+1)$
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
e.
$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$
$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$
f.
$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$
$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$
g.
$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$
$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$
$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$
$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$
h.
$x^6+2x^5+x^4-2x^3-2x^2+1$
$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$
$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$
AH
Akai Haruma
Giáo viên
24 tháng 6
Lời giải:
$(5.2^{13}.2^{22}-2^{36}):(3.2^{34})$
$=(5.2^{35}-2^{36}):(3.2^{34})=2^{35}(5-2):(3.2^{34})$
$=2^{35}.3:(3.2^{34})=2^{35}:2^{34}=2$
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2021
\(\Leftrightarrow\left(x^4+6x^3+6x^2\right)+\left(6x^3+36x^2+36x\right)+\left(6x^2+36x+36\right)=0\)
\(\Leftrightarrow x^2\left(x^2+6x+6\right)+6x\left(x^2+6x+6\right)+6\left(x^2+6x+6\right)=0\)
\(\Leftrightarrow\left(x^2+6x+6\right)^2=0\)
\(\Leftrightarrow x^2+6x+6=0\)
\(\Rightarrow x=-3\pm\sqrt{3}\)
16 tháng 8 2021
a: Ta có: x=31
nên x-1=30
Ta có: \(A=x^3-30x^2-31x+1\)
\(=x^3-x^2\left(x-1\right)-x^2+1\)
\(=x^3-x^3+x^2-x^2+1\)
=1
c: Ta có: x=16
nên x+1=17
Ta có: \(C=x^4-17x^3+17x^2-17x+20\)
\(=x^4-x^3\left(x+1\right)+x^2\left(x+1\right)-x\left(x+1\right)+20\)
\(=x^4-x^4-x^3+x^3+x^2-x^2-x+20\)
\(=20-x=4\)
16 tháng 8 2021
d: Ta có: x=12
nên x+1=13
Ta có: \(D=x^{10}-13x^9+13x^8-13x^7+...+13x^2-13x+10\)
\(=x^{10}-x^9\left(x+1\right)+x^8\left(x+1\right)-x^7\left(x+1\right)+...+x^2\left(x+1\right)-x\left(x+1\right)+10\)
\(=10-x\)
=-2
14 tháng 8 2021
d: Ta có: x=12
nên x+1=13
Ta có: \(D=x^{10}-13x^9+13x^8-13x^7+...+13x^2-13x+10\)
\(=x^{10}-x^9\left(x+1\right)+x^8\left(x+1\right)-x^7\left(x+1\right)+...+x^2\left(x+1\right)-x\left(x+1\right)+10\)
\(=x^{10}-x^{10}-x^9+x^9+x^8-x^8-x^7+...+x^3+x^2-x^2-x+1+9\)
\(=-x+10=-2\)
PT
1
CM
21 tháng 10 2017
⇔ 2 x 2 - 9x - 11 = 0 có hệ số a = 2, b = -9, c = -11
Ta có: a –b +c =2 – (-9) +(-11) =0
Suy ra nghiệm của phương trình là x 1 =-1 , x 2 = -c/a = -(-11)/2 =11/2
PT
1
CM
24 tháng 2 2019
Phương trình 1 3 x 2 + 2 x - 16 3 = 0 ⇔ x 2 +6x – 16 = 0 có hệ số a = 1, b = 6, c = -16
∆ '= 3 2 -1(-16) = 9 +16 =25 > 0
∆ ' = 25 =5
CM
16 tháng 6 2018
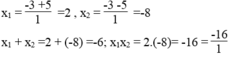
Ta có:
−13x2 + 22x − 13 = 0 (a = −13; b = 22; x = −13)
⇒ ∆ = b2 – 4ac = 222 – 4.(−13). (−13) = −192 < 0
nên phương trình vô nghiệm
Đáp án cần chọn là: B
Ta có x4-13x2+36=0
<=> x4-12x2+36-x2=0
<=> (x2-6)2-x=0
<=> (x2+x-6)(x2-x-6)=0
=> x2+x-6=0 hoặc x2-x-6=0
• x2+x-6=0 <=> x2-2x+3x-6=0
<=> x(x-2)+3(x-2)=0
<=> (x-2)(x+3)=0
=> x-2=0 hoặc x+3=0 => x=2 hoặc x=-3
• x2-x-6=0 <=> x2-3x+2x-6=0
<=> x(x-3)+2(x-3)=0
<=> (x-3)(x+2)=0
=> x-3=0 hoặc x+2=0 => x=3 hoặc x=-2
Vậy ...