Cho tam giác abc có góc bma = góc cma. M là trung điểm bc . Chứng minh tam giác abc cân..^,•
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


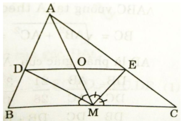
a) DM là đường phân giác của ΔABM nên theo tính chất đường phân giác của tam giác ta có:
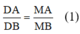
Tương tự EM là đường phân giác ΔACM nên:
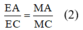
Mà MB = MC nên từ (1) và (2) suy ra

![]()
![]()
![]()
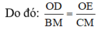
![]()

a, Vì MD là phân giác AMB \(\Rightarrow\frac{AD}{AM}=\frac{BD}{BM}\)\(\Rightarrow\frac{AD}{BD}=\frac{AM}{BM}\)\(\Rightarrow\frac{AD}{BD}=\frac{AM}{CM}\)(MB = MC)
Vì ME là phân giác AMC \(\Rightarrow\frac{AE}{AM}=\frac{EC}{MC}\)\(\Rightarrow\frac{AE}{EC}=\frac{AM}{MC}\)
\(\Rightarrow\frac{AE}{EC}=\frac{AD}{BD}\) => DE // BC (định lý Thales đảo)
b, Vì DE // BE (cmt) \(\Rightarrow\frac{DO}{BM}=\frac{AO}{OM}\)(Hệ quả định lý Thales) và \(\frac{OE}{MC}=\frac{OA}{OM}\) (Hệ quả định lý Thales)
\(\Rightarrow\frac{DO}{BM}=\frac{OE}{MC}\)
Mà BM = MC (gt)
=> DO = OE

a) Vì AM là trung tuyến của \(\Delta ABC\Rightarrow BM=CM;M\in BC\)
Xét \(\Delta ABM\)có MD là p/g \(\widehat{BMA}\Rightarrow\frac{AD}{BD}=\frac{AM}{BM}\)hay \(\frac{AD}{BD}=\frac{AM}{CM}\left(1\right)\)
Xét \(\Delta ACM\)có ME là p/g \(\widehat{CMA}\Rightarrow\frac{AE}{CE}=\frac{AM}{CM}\left(2\right)\)
Từ (1)(2)\(\Rightarrow\frac{AD}{BD}=\frac{AE}{CE}\Rightarrow DE//BC\)(đ/ lí Ta-lét đảo)
b) Có \(DE//BC\), \(O\in DE,M\in BC\Rightarrow OD//BM;OE//CM\)
Xét \(\Delta ABM\)có \(OD//BM\Rightarrow\frac{OD}{BM}=\frac{OA}{AM}\left(3\right)\)
Xét \(\Delta ACM\)có \(OE//CM\Rightarrow\frac{OE}{CM}=\frac{OA}{AM}\left(4\right)\)
Từ (3)(4) \(\Rightarrow\frac{OD}{BM}=\frac{OE}{CM}\).Mà BM=CM \(\Rightarrow OD=OE\)

Tam giác ABC có :
BM=CM(GT)
\(\widehat{BAM}=\widehat{CAM}\left(gt\right)\)
Một tam giác có tia phân giác đồng thời là đường trung tuyến thì là tam giác cân
=> Tam giác ABC cân tại A (đccm)
Ok cách khác
Kẻ \(MD\perp AB;ME\perp AC\)
Xét tam giác ADM và AEM, có :
\(\widehat{ADM}=\widehat{AEM}=90^o\)
\(\widehat{BAM}=\widehat{CAM}\left(gt\right)\)
AM-cạnh chung
=> Tam giác ADM=AEM(cạnh huyền-góc nhọn)
=> DM=ME
Xét tam giác BMD và CME,có :
DM=ME(cmt)
\(\widehat{MEC}=\widehat{MDB}=90^o\)
BM=CM(gt)
=> Tam giác BMD=CME(cạnh huyền-cạnh góc vuông)
=> \(\widehat{B}=\widehat{C}\)
=> Tam giác ABC cân tại A (2 góc đáy bằng nhau)
*Hơi dài dòng TÍ

a: Xét ΔABI và ΔACI có
AB=AC
\(\widehat{BAI}=\widehat{CAI}\)
AI chung
Do đó: ΔABI=ΔACI
Ta có: ΔABC cân tại A
mà AI là đường trung tuyến
nên AI là đường phân giác
b: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
c: Ta có: ΔABC cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
mình chưa học đến bài tam giác cân thì có bài làm nào khác không ạ?
Xét tam giác AMB và AMC có
AM là cạnh chung
BM=MC(gt)
góc BMA=CMA (gt)
=>Tam giác AMB=tam giác AMC (c.g.c)
=>AB=AC
=>Tam giác ABC cân tại A ( dpcm)