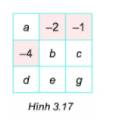
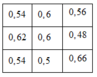
Cho bảng vuông 4x4.Thay các chữ bằng các số thích hợp sao cho tổng các số trong mỗi hàng,mỗi cột,mỗi đường chéo bằng 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
2 tháng 10 2023
a) Tổng các số trong bảng = Tổng các hàng
Mà tổng các hàng bằng 0 nên tổng các số trong bảng đó bằng 0.
b) Xét hàng số 1 ta có:
a + (-2) + (-1) = 0 => a + (-3) = 0 => a = 3
Xét cột số 1 ta có:
3 + (-4) + d = 0 => (-1) + d = 0 => d = 1.
Xét đường chéo chứa b và d có:
(-1) + b + d = 0 => (-1) + b +1 = 0 => b = 0.
Xét cột số 2 ta có:
(-2) + 0 + e = 0 => e = 2
Xét dòng số 2 có:
-4 + b + c = 0 => -4 + 0 + c = 0 => c =4
Xét dòng số 3 có:
d + e + g = 0 => 1 + 2 + g = 0 => g = -3
DD
Đoàn Đức Hà
Giáo viên
28 tháng 5 2022
Trên mỗi hàng, mỗi cột phải có hai số -1, hai số 1.
Ta sẽ xếp theo hàng.
Ta có các khả năng của các hàng như sau:
(1) 1, 1, -1, -1
(2) 1, -1, -1, 1
(3) -1, -1, 1, 1
(4) -1, 1, -1, 1
(5) 1, -1, 1, -1
(6) -1, 1, 1, -1
Giả sử hàng 1 ta điền bộ (1). Ta có các trường hợp sau:
TH1: Hàng 2 điền bộ (1), khi đó hàng 3, hàng 4 ta phải điền bộ (3).
TH2: Hàng 2 điền bộ để tổng 2 số trong của các cột bằng 0, khi đó ta điền bộ (3). Hàng 3 và hàng 4 khi đó cũng phải điền sao cho tổng các cột trong hai hàng bằng 0. Có 6 cách điền như vậy.
TH3: Hàng 2 điền sao cho có 2 cột trong 4 cột có tổng bằng 0. Có 4 cách. Khi đó điền hàng 3 có 2 cách, điền hàng 4 có 1 cách. Tổng số cách là: 1.4.2.1=8 (cách).
Vậy có tổng số cách là: 6.(1 + 6 + 8) = 90 (cách).
NH
Cách sắp xếp các số từ 1 đến 16 vào hình vuông 4x4 sao cho tổng mỗi hàng, cột, đường chéo bằng nhau?
3
2 tháng 8 2016
các số sắp xếp như sau:
1 14 15 4
12 7 6 9
8 11 10 5
12 2 3 16
tổng mỗi hàng, cột, chéo là 34
2 tháng 8 2016
các số sắp xếp như sau:
1 14 15 4
12 7 6 9
8 11 10 5
12 2 3 16
tổng mỗi hàng, cột, chéo là 34
16 tháng 4 2016
Giá trị nhỏ nhất của mỗi tổng là: -1 + -1 + -1 + -1+ -1 = -5
Giá trị lớn nhất của mỗi tổng là : 1+1+1+1+1=5
=> Số giá trị mà mỗi tổng có thể nhận được là : [5 - (-5) ] +1 = 11 giá trị
có 5 tổng theo hàng ngang, 5 tổng theo hàng dọc, 2 tổng theo hàng chéo
=> có tất cả 12 tổng nhận 11 giá trị
=> theo nguyên lý ĐRL thì có ít nhất 2 tổng bằng nhau