Ai giải giúp mình bài này với mình cần gấp sáng mai
Cho ( O ), điểm K nằm ngoài ( O ). Kẻ các tiếp tuyến KA, KB với ( O ). Kẻ đường kính AOC, tiếp tuyến của ( O ) tại C cắt AB ở E. CMR:
a, \(\Delta KBC\)đồng dạng với \(\Delta OBE\)
b, CK \(\perp\) OE

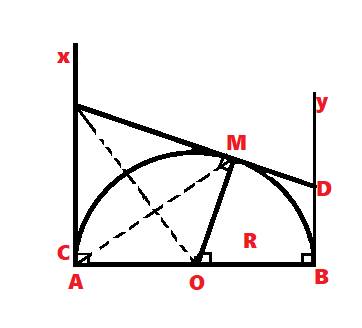
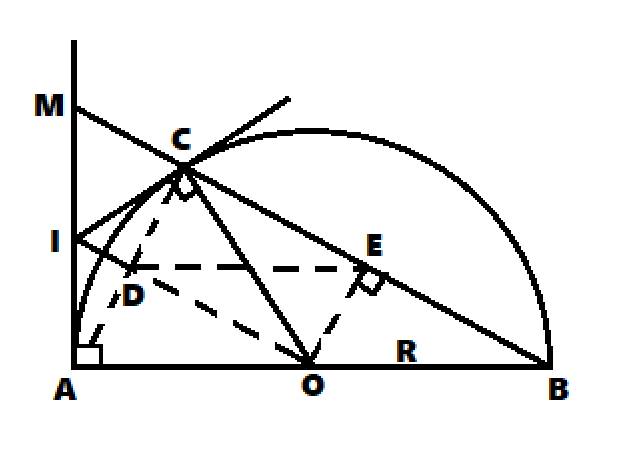
Vẽ hình giúp mình luôn nha cảm ơn nhiều