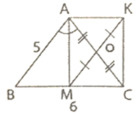
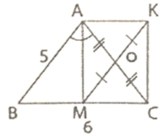
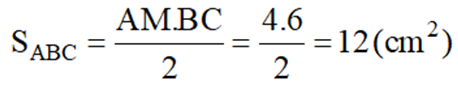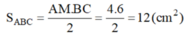cho tam giác ABC cân tại A có AB=5cm,BC=6cm , phân giác AM (M thuộc BC).Gọi O là trung điểm của AC ,K là điểm đối xứng của M qua O.
a)Tính diện tích tam giác ABC
b)chứng minh AK // MC
c)tứ giác AMCK là hình gì? Vì sao?
d)tam giác ABC có điều kiện gì thì AMCK là hình vuông.