Cho \(E=1.2.3+2.3.4+...+n\left(n+1\right)\left(n+2\right).\)( n \(\in\)N*). CMR : 4E + 1 luôn là bình phương của một số tự nhiên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
3 tháng 8 2023
4S=1.2.3.4+2.3.4.4+3.4.5.4+...+k(k+1)(k+2).4=
=1.2.3.4+2.3.4(5-1)+3.4.5.(6-2)+...+k(k+1)(k+2)[(k+3)-(k-1)]=
=1.2.3.4-1.2.3.4+2.3.4.5-2.3.4.5+3.4.5.6-...-(k-1)k(k+1)(k+2)+k(k+1)(k+2)(k+3)=
=k(k+1)(k+2)(k+3)=k(k+3)(k+1)(k+2)=
=(k2+3k)(k2+3k+2)=(k2+3k)2+2(k2+3k)
=> 4S+1=(k2+3k)2+2(k2+3k)+1=[(k2+3k)+1]2
11 tháng 2 2019
S1= 1.2.3
S2= 2.3.4
S3=3.4.5
...........
Sn = n(n+1)(n+2)
S= S1+S2+S3+...+Sn
Chứng minh 4S + 1 là 1 số chính phương
11 tháng 2 2019
\(S=1\cdot2\cdot3+2\cdot3\cdot4+3\cdot4\cdot5+...+k\left(k+1\right)\left(k+2\right)\)
\(\Rightarrow4S=1\cdot2\cdot3\cdot4+2\cdot3\cdot4\cdot4+3\cdot4\cdot5\cdot4+...+k\left(k+1\right)\left(k+2\right)\cdot4\)
\(=1\cdot2\cdot3\left(4-0\right)+2\cdot3\cdot4\left(5-1\right)+3\cdot4\cdot5\left(6-2\right)+.....+k\left(k+1\right)\left(k+2\right)\left[\left(k+3\right)-\left(k-1\right)\right]\)\(=1\cdot2\cdot3\cdot4-0\cdot1\cdot2\cdot3+2\cdot3\cdot4\cdot5-1\cdot2\cdot3\cdot4+....+k\left(k+1\right)\left(k+2\right)\left(k+3\right)-\left(k-1\right)k\left(k+1\right)\left(k+2\right)\)\(=k\left(k+1\right)\left(k+2\right)\left(k+3\right)\)
Ta cần chứng minh:\(k\left(k+1\right)\left(k+2\right)\left(k+3\right)+1\) là số chính phương.
Thật vậy:\(k\left(k+1\right)\left(k+2\right)\left(k+3\right)+1=\left[k\left(k+3\right)\right]\left[\left(k+1\right)\left(k+2\right)\right]+1\)
\(=\left(k^2+3k\right)\left(k^2+3k+2\right)+1\left(1\right)\)
Đặt \(k^2+3k=t\) thì (1) sẽ trở thành:
\(t\left(t+2\right)+1=t^2+2t+1=\left(t+1\right)^2=\left(k^2+3k+1\right)^2\)
Vì \(k\in N\)nên \(\left(k^2+3k+1\right)^2\) là số chính phương hay \(4S+1\) là số chính phương.
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 12 2018
\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{n\left(n+1\right)\left(n+2\right)}=\dfrac{637}{2550}\)
\(\Leftrightarrow\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...+\dfrac{1}{n\left(n+1\right)}-\dfrac{1}{\left(n+1\right)\left(n+2\right)}\right)=\dfrac{637}{2550}\)
\(\Leftrightarrow\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{\left(n+1\right)\left(n+2\right)}\right)=\dfrac{637}{2550}\)
\(\Leftrightarrow\dfrac{1}{1.2}-\dfrac{1}{\left(n+1\right)\left(n+2\right)}=\dfrac{637}{1275}\)
\(\Leftrightarrow\dfrac{1}{\left(n+1\right)\left(n+2\right)}=\dfrac{1}{2}-\dfrac{637}{1275}=\dfrac{1}{2550}\)
\(\Leftrightarrow\left(n+1\right)\left(n+2\right)=2550\)
\(\Leftrightarrow n^2+3n-2548=0\)
\(\Rightarrow n=49\)
NP
1
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 2 2020
- Với \(n=1\Rightarrow1.2.3=\frac{1.2.3.4}{4}\) (đúng)
- Giả sử biểu thức đúng với \(n=k\) hay:
\(1.2.3+...+k\left(k+1\right)\left(k+2\right)=\frac{k\left(k+1\right)\left(k+2\right)\left(k+3\right)}{4}\)
Ta cần chứng minh nó đúng với \(n=k+1\) hay:
\(1.2.3+...+k\left(k+1\right)\left(k+2\right)+\left(k+1\right)\left(k+2\right)\left(k+3\right)=\frac{\left(k+1\right)\left(k+2\right)\left(k+3\right)\left(k+4\right)}{4}\)
Thật vậy, ta có:
\(1.2.3+...+k\left(k+1\right)\left(k+2\right)+\left(k+1\right)\left(k+2\right)\left(k+3\right)\)
\(=\frac{k\left(k+1\right)\left(k+2\right)\left(k+3\right)}{4}+\left(k+1\right)\left(k+2\right)\left(k+3\right)\)
\(=\left(k+1\right)\left(k+2\right)\left(k+3\right)\left[\frac{k}{4}+1\right]\)
\(=\left(k+1\right)\left(k+2\right)\left(k+3\right).\frac{\left(k+4\right)}{4}\)
\(=\frac{\left(k+1\right)\left(k+2\right)\left(k+3\right)\left(k+4\right)}{4}\) (đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1
Bài toán chia kẹo kinh điển đây mà.
Trước hết chúng ta đếm 1 chút theo kiểu lớp 1 lớp 2 gì đó: có 1 đoạn thẳng, cần chia đoạn thẳng ấy làm 3 phần, vậy cần chấm lên đoạn thẳng ấy mấy điểm? Câu trả lời rõ ràng là 2 điểm. Cần chia 1 con cá thành 3 khúc, ta cần 2 nhát cắt; cần ngăn 4 con cọp xếp hàng ngang để chúng đỡ cắn nhau, ta cần 3 vách ngăn. Hay để chia 1 đối tượng làm n phần, ta cần dùng n-1 vách ngăn để chia nó ra, Như thế này:
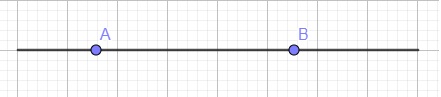
Bây giờ có số tự nhiên n, ta phân tích nó như sau:
\(n=1+1+1+...+1+1+1\)
Giả sử ta "vách ngăn" vào một vài vị trí giữa các số 1, kiểu thế này:
\(1+1+\left|1+1+1\right|+1+|1+1+...+1\)
Rõ ràng với 3 vách ngăn trên, ta chia n thành 3+1=4 phần, mỗi phần đều có giá trị nguyên dương, lần lượt là 2,3,1,n-6.
Bây giờ cần chia dãy \(1+1+...+1\) trên thành m phần, vậy cần đặt bao nhiêu vách ngăn? Cũng như ban đầu đã phân tích, ta cần đặt \(m-1\) tấm vách ngăn.
Ta có bao nhiêu vị trí để đặt \(m-1\) vách ngăn nói trên? Có n số 1, ta sẽ có \(n-1\) vị trí đặt vách ngăn, sao cho giữa 2 vách ngăn có ít nhất một số 1 (hay giữa 2 vách ngăn luôn là 1 giá trị nguyên dương).
Tóm lại, để chia dãy tổng \(1+1+...+1\) (n số hạng) thành m phần, sao cho mỗi phần chứa ít nhất một số 1, ta cần đặt \(m-1\) tấm vách ngăn vào \(n-1\) vị trí khả dĩ. Như vậy, ta có \(C_{n-1}^{m-1}\) cách.
Hiển nhiên, giá trị của mỗi phần (tức là tổng các số 1 trong phần đó) chính là giá trị nghiệm \(x_i\) của pt \(\sum\limits^m_{i=1}x_i=n\). Vậy pt có \(C_{n-1}^{m-1}\) nghiệm nguyên dương.
//Bay giờ tới nghiệm tự nhiên thì đơn giản, số tự nhiên khác số nguyên dương đúng 1 số 0, bây giờ ta "loại" nó đi là ra bài toán bên trên. Bằng cách đặt \(y_1=x_1+1;y_2=x_2+1...;y_m=x_m+1\), ta đảm bảo \(y_i\) luôn nguyên dương khi \(x_i\) tự nhiên.
Khi đó:
\(y_1+y_2+...+y_m=\left(x_1+1\right)+\left(x_2+1\right)+...+\left(x_m+1\right)\)
\(=\left(x_1+x_2+...+x_m\right)+m=n+m\)
Quay về bài trên, ta có pt \(y_1+y_2+...+y_m=n+m\) có \(C_{n+m-1}^{m-1}\) nghiệm.
Ứng với mỗi \(y_i\) cho đúng 1 giá trị \(x_i=y_i-1\) tương ứng, do đó pt:
\(\sum\limits^m_{i=1}x_i=n\) có \(C_{n+m-1}^{m-1}\) nghiệm tự nhiên
Công thức đầu của em có vẻ bị sai :D
6 tháng 1
Wow, big brain, cảm ơn thầy nhiều ;) (mà hình như 2 công thức đó bằng nhau vì \(C^k_n=C^{n-k}_n\) ấy thầy).
PT
1
15 tháng 7 2018
Đặt \(A=\frac{1}{1.2.3}+\frac{1}{2.3.4}+....+\frac{1}{n\left(n+1\right)\left(n+2\right)}\)
\(\Rightarrow2A=\frac{2}{1.2.3}+\frac{2}{2.3.4}+....+\frac{2}{n\left(n+1\right)\left(n+2\right)}\)
\(=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+...+\frac{1}{n\left(n+1\right)}-\frac{1}{\left(n+1\right)\left(n+2\right)}\)
\(=\frac{1}{1.2}-\frac{1}{\left(n+1\right)\left(n+2\right)}\)
\(=\frac{1}{2}-\frac{1}{\left(n+1\right)\left(n+2\right)}\)
\(=\frac{\left(n+1\right)\left(n+2\right)-2}{2\left(n+1\right)\left(n+2\right)}\)
\(\Rightarrow A=\frac{\left(n+1\right)\left(n+2\right)-2}{4\left(n+1\right)\left(n+2\right)}\)
TK nha!!
Ta có: \(E=1.2.3+2.3.4+.....+n\left(n+1\right)\left(n+2\right)\)
\(\Rightarrow4E=1.2.3.4+2.3.4.\left(5-1\right)+......+n\left(n+1\right)\left(n+2\right)\left[\left(n+3\right)-\left(n-1\right)\right]\)
\(\Rightarrow4E=1.2.3.4+2.3.4.5-1.2.3.4+....+\) \(n\left(n+1\right)\left(n+2\right)\left(n+3\right)-\left(n-1\right)n\left(n+1\right)\left(n+2\right)\)
\(\Rightarrow4E=n\left(n+1\right)\left(n+2\right)\left(n+3\right)\)
\(\Rightarrow4E=n\left(n+3\right)\left(n+1\right)\left(n+2\right)=\left(n^2+3n\right)\left(n^2+3n+2\right)\)
Đặt n2 + 3n +1 = y
\(\Rightarrow4E+1=\left(y-1\right)\left(y+1\right)+1=y^2-1+1=y^2\)
\(\Rightarrow4E+1=\left(n^2+3n+1\right)^2\)
Vì n tự nhiên => n2 + 3n + 1 tự nhiên => 4E + 1 là số chính phương
=> đpcm.