Cho hai số dương x,y thỏa mãn: 2x2+xy-y2=0. Tính giá trị biểu thức:
A = \(\frac{x^2y+xy^2}{x^3+y^3}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 2 2019
Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
<=> 
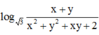
(2)
Đặt 
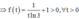
=> f(t) đồng biến trên (0;+∞)
<=> 
<=> 
Khi đó,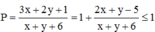 
vì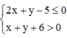 
Vậy Pmax = 1 khi và chỉ khi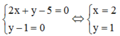 
CM
13 tháng 9 2019
Đáp án C
Phương pháp giải:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Lời giải:
log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y (1)
(2)
Đặt 
=> f(t) đồng biến trên (0;+∞)
Khi đó, 
vì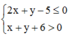 
Vậy Pmax = 1 khi và chỉ khi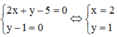 
HM
0
CM
25 tháng 11 2019
Chọn A.
Phương pháp:
- Biến đổi điều kiện bài cho về dạng f u = f v với u, v là các biểu thức của x, y.
- Xét hàm f t suy ra mối quan hệ của u, v rồi suy ra x, y.
- Đánh giá P theo biến t=x+y bằng cách sử dụng phương pháp hàm số.
Cách giải:
SM
25 tháng 4 2018
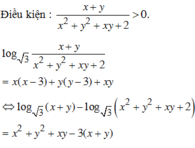
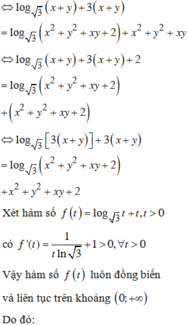
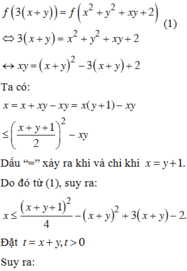
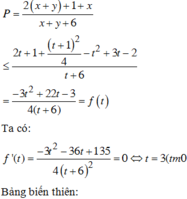
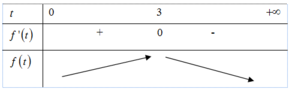
Nhận xét :
x2 lớn hơn 0 ( với mọi x dương )
y2 lớn hơn 0 ( với mọi y dương )
Để Amin => \(\frac{1}{x^2}+\frac{1}{y^2}\) Min => x2 và y2 max
Nhưng x + y = 2
=> x = y = 1
A min = \(\frac{1}{1}+\frac{1}{1}+\frac{3}{1}=5\)
Vậy A min = 5 <=> x = y = 1
25 tháng 4 2018
\(A=\frac{1}{x^2}+\frac{1}{y^2}+\frac{3}{xy}\) và x + y = 2
AM-GM => x + y >= \(2\sqrt{xy}\)
=> \(2\sqrt{xy}\)<= 2
=> xy <= 1
\(\frac{1}{x^2}+\frac{1}{y^2}\ge\frac{1}{xy}\)
=> A >= 1/xy + 3/xy
=> A >= 4/xy
mà xy <= 1
=> A >= 4/1
=> A>= 4
dấu bằng sảy ra khi x = y = 2/2 = 1
Vậy GTNN của A là 4 khi x = y = 1
CM
17 tháng 10 2017
Ta có ( x + y ) 2 = x 2 + y 2 + 2 x y = 4 − 2 3 = ( 3 − 1 ) 2 ⇒ x + y = 3 − 1.
Suy ra P = x + y = 3 − 1 k h i x + y ≥ 0 1 − 3 k h i x + y < 0 .