Cho một đường tròn (O) và một điểm A cố định Thuộc đường tròn kẻ tiếp tuyến AT và lấy trên At một điểm M Từ M kẻ Tiếp tuyến thứ hai với MB và đường tròn tìm tập hợp tâm đường tròn ngoại tiếp tam giác MAB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 8 2017
Gọi I là giao điểm của MN và AC.
Ta có: \(\widehat{IHO}=\widehat{OEI}=90°\)
\(\Rightarrow\)Tứ giác EIHO nội tiếp đường tròn.
\(\Rightarrow\)Tâm của đường tròn ngoại tiếp ∆OHE nằm trên đường trung trực của EI.(*)
Ta có ∆AIH \(\approx\)∆AOE
\(\Rightarrow\)AH.AO = AE.AI (1)
Ta có: ∆AMB \(\approx\)AOM
\(\Rightarrow\)AM2 = AH.AO (2)
Ta lại có: ∆ABM \(\approx\)∆AMC
\(\Rightarrow\)AM2 = AB.AC (3)
Từ (1), (2), (3) \(\Rightarrow\)AE.AI = AB.AC
Vì A,B,C,E cố định nên I cố định (**)
Từ (*), (**) suy ta tâm đường tròn ngoại tiếp ∆OHE nằm trên đường trung trực của EI.
PS: không chứng minh được nó nằm trên đường tròn nha b. Hình tự vẽ.
1 tháng 8 2023
a: Xét ΔMCD và ΔMEC có
góc MCD=góc MEC
góc CMD chung
=>ΔMCD đồng dạng với ΔMEC
b: Xét (O) có
MA,MC là tiếp tuyến
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC tại K
ΔMCO vuông tại C có CK là đường cao
nên MK*MO=MC^2
c: góc AOC=2*góc AIC=120 độ
=>góc AOM=góc COM=60 độ
Xét ΔCOM vuông tại C có tan COM=CM/CO
=>CM/R=căn 3
=>CM=R*căn 3
CM
26 tháng 4 2018
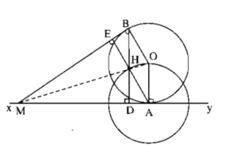
Tứ giác AOBH có BH // OA, AH // OB và OA = OB nên là hình thoi.
CM
25 tháng 12 2018
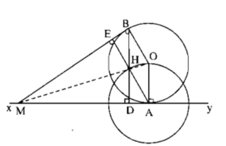
Gọi BD, AE là đường cao của ∆ MAB. Ta có ΔMAE = ∆ MBD (cạnh huyền – góc nhọn) nên ME = MD, ∆ MHE = ∆ MHD (cạnh huyền – cạnh góc vuông) nên ∠ (EMH) = ∠ (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.
4 tháng 1 2022
a: \(MA=3\sqrt{3}\left(cm\right)\)
b: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO\(\perp\)AB