Một người đứng ở một đỉnh dốc bờ biển ném một hòn đá ra biển. Hỏi người ấy phải ném hòn đá dưới một góc bằng bao nhiêu so với phương nằm ngang để nó rơi xa chân bờ biển nhất. Khoảng cách xa nhất ấy là bao nhiêu? Cho biết bở dốc thẳng đứng, hòn đá được ném từ độ cao H =20m so với mặt nước và có vận tốc đầu là vo = 14m/s. Lấy g = 9,8m/s²
giúp mình bài này với!Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Thời gian hòn đá rơi chạm mặt nước biển:
\(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot10}{9,8}}=\dfrac{10}{7}s\approx1,43s\)
b)Tầm xa của vật: \(L=v_0\sqrt{\dfrac{2h}{g}}=5\cdot\sqrt{\dfrac{2\cdot10}{9,8}}=\dfrac{50}{7}m\)
Vận tốc vật khi chạm mặt nước biển:
\(v=v_0+gt=5+9,8\cdot\dfrac{10}{7}=19m/s\)

Đáp án: A
Chọn gốc tọa độ tại mặt đất, Ox nằm ngang, Oy hướng thẳng đứng lên trên. Gốc thời gian là lúc ném hòn đá.
t là thời gian hòn đá chuyển động.
Ta có:
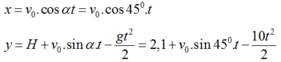
Khi chạm đất thì:
![]()
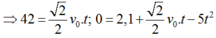
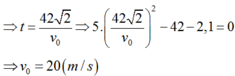

Đáp án A
Chọn gốc tọa độ tại mặt đất, Ox nằm ngang, Oy hướng thẳng đứng lên trên. Gốc thời gian là lúc ném hòn đá.
t là thời gian hòn đá chuyển động.
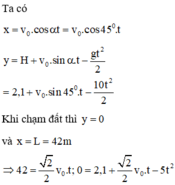
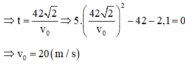

a)Qũy đạo của hòn đá: \(y=25+v_0sin\alpha\cdot t-\dfrac{1}{2}gt^2\)
Thời gian chuyển động của hòn đá:
\(\Rightarrow0=25+v_0\cdot sin\alpha\cdot t-\dfrac{1}{2}gt^2\)
\(\Rightarrow0=25+15\cdot sin30\cdot t-\dfrac{1}{2}\cdot10\cdot t^2\)
\(\Rightarrow t\approx3,11s\)
b)Khoảng cách từ chân tháp đến chỗ rơi:
\(S=x=v_0\cdot cos\alpha\cdot t\)
\(\Rightarrow S=15\cdot sin30\cdot3,11=23,325m\)
c)Ta có: \(v_x=v_0\cdot cos\alpha\)
\(v_y=v_0\cdot sin\alpha-gt\)
Vận tốc hòn đá lúc chạm đất:
\(v=\sqrt{(v_0\cdot sin\alpha)^2+\left(v_0\cdot sin\alpha-gt\right)^2}\)
\(=\sqrt{\left(15\cdot sin30\right)^2+\left(15\cdot sin30-10\cdot3,1\right)^2}\)
\(\approx24,7\)m/s
ở trên cho vx=v0⋅cosα sao xuống dưới chuyển thành sin rồi, v của bài này là 26,94 m/s ấy.

a)Phương trình quỹ đạo: \(y=\dfrac{g}{2v_0^2}x^2=\dfrac{9,8}{2\cdot5^2}x^2=0,196x^2\)
b)Thời gian hòn đá chạm mặt nước biển: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot10}{9,8}}=2,04s\)
c)Tầm xa vật: \(L=x_{max}=v_0t\)
Tọa độ Ox: \(\left\{{}\begin{matrix}v_{0x}=v_0\\a_x=0\\v_x=v_0\end{matrix}\right.\)
Tọa độ Oy: \(\left\{{}\begin{matrix}v_{0y}=0\\a_y=g\\v_y=gt\end{matrix}\right.\)
Độ lớn vận tốc: \(v=\sqrt{\left(gt\right)^2+v_0^2}\)
c)Sau 1s:
Tầm xa: \(L=v_0t=5\cdot1=5m\)
Độ lớn: \(v=\sqrt{\left(gt\right)^2+v_0^2}=\sqrt{\left(9,8\cdot1\right)^2+5^2}=11m/s\)

* Tóm tắt : | Giải :
\(v_0=12\) m/s | a, Thời gian hòn đá chạm mặt biển :
\(h=19,6m\) | \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2.19,6}{9,8}}=2\left(s\right)\)
\(g=9,8\) (m/s2) | b, Tầm Xa của hòn đá :
( đề ko cho, tức | \(L=v_o.t=12.2=24\left(m\right)\)
là g = 9,8)
----------
a, \(t=?\left(s\right)\)
b, \(L=?\left(m\right)\)\(\)

