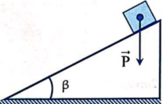
một chiếc hộp có trọng lượng 50N bắt đầu trượt không vận tốc đầu từ một mặt phẳng nghiên cao 15m, dài 10m. Độ giảm thế năng của chiếc hộp khi nó trượt đến mặt phẳng nghiên là bao nhieeu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


chọn ý B vì vật chịu thêm tác dụng của lực ma sát cơ năng của vật sẽ thay đổi. Công của lực ma sát bằng độ biến thiên cơ năng của vật

Chọn mốc thế năng tại chân mặt phẳng nghiêng.
a) Cơ năng tại đỉnh mặt phẳng nghiêng
\(W=mgh=mg.AB\sin 30^0=1,2.10.AB.\sin 30^0=24\)
\(\Rightarrow AB = 4(m)\)
b) Tại D động năng bằng 3 lần thế năng, ta có: \(W_đ=3W_t\Rightarrow W = 4W_t \Rightarrow W_t = 24: 4 = 6(J)\)
\(\Rightarrow mgh_1=mg.DB\sin 30^0=1,2.10.DB.\sin 30^0=6\)
\(\Rightarrow DB = 1(m)\)
c) Tại trung điểm mặt phẳng nghiêng
Thế năng: \(W_t = mgh_2=mg.\dfrac{AB}{2}\sin 30^0=1,2.10.2.\sin 30^0=12(J)\)
Động năng: \(W_đ=W-W_t=24-12=12(J)\)
\(\Rightarrow \dfrac{1}{2}.1,2.v^2=12\)
\(\Rightarrow 2\sqrt 5(m/s)\)
d) Công của lực ma sát trên mặt ngang: \(A_{ms}=\mu mg.S\)
Theo định lí động năng: \(W_{đ2}-W_{đ1}=-A_{ms}\Rightarrow 0-24=-\mu.1,2.10.1\Rightarrow \mu = 2\)
anh ơi , anh quên tính vận tốc của vật tại chân mặt phẳng nghiêng kìa . Đãng trí quá .![]()

Chọn hệ trục tọa độ \(Oxy\) gồm:
- \(Oy\) vuông góc với mặt phẳng nghiêng
- \(Ox\) song song với mặt phẳng nghiêng
- Lấy gốc thời gian lúc vật bắt đầu trượt xuống mặt phẳng nghiêng
Các lực tác dụng lên vật khi nó trượt xuống mặt phẳng nghiêng:
+ Trọng lực \(\overrightarrow{P}\), phản lực \(\overrightarrow{Q}\), lực ma sát \(\overrightarrow{F_{ms}}\)
Áp dụng định luật II Newton cho vật: \(\overrightarrow{a}=\dfrac{\overrightarrow{P}+\overrightarrow{Q}+\overrightarrow{F_{ms}}}{m}\) \(\left(1\right)\)
Chiếu (1) lên \(Ox\): \(a=\dfrac{P.\sin30-F_{ms}}{m}\) \(\left(2\right)\)
Mà \(F_{ms}=\mu.N=\mu.Q\)
Chiếu (1) lên \(Oy\): \(O=\dfrac{-P.\cos30+Q}{m}\)
\(\Rightarrow Q=P.\cos30\)
\(\Rightarrow F_{ms}=\mu.P.\cos30\)
Thay vào (2): \(a=\dfrac{P.\sin30-\mu.P.\cos30}{m}\) \(=\dfrac{m.g\left(\sin30-\mu.\cos30\right)}{m}\)
\(\Rightarrow a=g\left(\sin30-\mu.\cos30\right)\) \(=10\left(\dfrac{1}{2}-0,2.\dfrac{\sqrt{3}}{2}\right)=3,268\) (m/s2)
Ta có: \(S=\dfrac{1}{2}at^2\Rightarrow t=\sqrt{\dfrac{2S}{a}}\left(3\right)\)
Áp dụng hệ thức lượng ta có:
\(\sin30=\dfrac{h}{l}\Rightarrow h=\sin30.l\) \(=sin30.5=2,5\left(m\right)\)
Thay vào (3) ta có: \(t=\sqrt{\dfrac{2S}{a}}=\sqrt{\dfrac{2.2,5}{3,286}}\approx1,233\left(s\right)\)
Vậy vận tốc ở chân mặt phẳng nghiêng là 1,233 giây

Cơ năng tại chân dốc B: \(W_B=\dfrac{1}{2}mv^2_B\)
Cơ năng tại đỉnh dốc A: \(W_A=mgh\)
Công ma sát: \(A=-F_{ms}\cdot l=\mu N\cdot l=\mu.mg.cos\alpha.l\)
Bảo toàn cơ năng: \(A_{ms}=W_B-W_A\)
\(\Rightarrow W_A=mgh=-A_{ms}=0,1\cdot0,5\cdot10\cdot cos30^o\cdot0,14=0,07\dfrac{\sqrt{3}}{2}\left(J\right)\)
cho em hỏi sao ta ko thể tính thế năng = mgh = 0,5.10.0,14.sin30 ạ

\(v_2=\sqrt{2as}=10\left(m/s\right)\) ( hoặc bảo toàn cơ năng tại đỉnh và chân dốc cũng dễ tính đc vận tốc )
Dễ tính đc a như sau: Thành phần kéo vật đi xuống là Px ( trong đó có trọng lực và phản lực tác dụng vào vật)
\(P_x=ma\Rightarrow P\sin\alpha=ma\Rightarrow a=5\left(m/s^2\right)\)
a) Độ biến thiên động năng: \(W_{đ2}-W_{đ1}=\dfrac{1}{2}mv_2^2-\dfrac{1}{2}mv_1^2=100\left(J\right)\) ( v1=0 )
b) Dễ tính đc h=5m ( Vì sina=h/l => h=5m )
Áp dụng định luật bảo toàn cơ năng: ( vì vật chỉ chịu tác dụng của trọng trường )
\(W_1=W_2\Leftrightarrow mgh=2mgh'\Leftrightarrow h'=\dfrac{5}{2}\left(m\right)\)

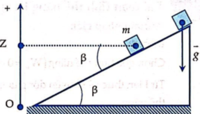
+ Chọn mốc tính thế năng tại vị trí chân mặt phẳng nghiêng
+ Tính giá trị đạỉ số độ cao Z của vật so với mốc:
- Gia tốc của vật trượt không ma sát trên mặt phẳng nghiêng
![]()
- Quãng đường vật trượt sau 2 giây bằng:
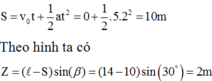
+ Vậy thế năng trọng trường của vật ở thời điểm t = 2 giây bằng
![]()

Chọn mốc thế năng tại mặt nằm ngang BC
a. Ta có cotan α = B H A H = 0 , 6 0 , 1 = 6
Mà W A = m . g . A H = m .10.0 , 1 = m ( J ) ; W B = 1 2 m v B 2 ( J ) A m s = μ m g cos α . A B = 0 , 1. m .10. cos α . A H sin α = m . c o tan α .0 , 1 = 0 , 6 m ( J )
Theo định luật bảo toàn năng lượng
W A = W B + A m s ⇒ m = 1 2 m v B 2 + 0 , 6 m ⇒ v B = 0 , 8944 ( m / s )
b. Theo định luật bảo toàn năng lượng
⇒ m = 1 2 m v B 2 + 0 , 6 m ⇒ v B = 0 , 8944 ( m / s )
Mà W A = m g . A H = m .10.0 , 1 = m ( J ) ; W C = 0 ( J ) A m s = μ m g cos α . A B + μ m g . B C = 0 , 6 m + m . B C ⇒ m = 0 + 0 , 6 m + m . B C ⇒ B C = 0 , 4 ( m )