Đa thức thích hợp điền vào chỗ trống trong đẳng thức:
\(\frac{...}{x^2-9}=\frac{x}{x+3}\)
*Giải thích từng bước giúp mình nhé!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{x^2-2xy+y^2}{x+y}=\frac{P}{x^2-y^2}\)
\(\frac{\left(x-y\right)^2}{x+y}=\frac{P}{\left(x-y\right)\left(x+y\right)}\)
\(P=\frac{\left(x-y\right)^3\left(x+y\right)}{x+y}=\left(x-y\right)^3\)

Ta có: x - x 2 = x 1 - x
(Tử thức của phân thức bên phải bằng tử thức của phân thức bên trái chia cho (1 – x).
Do đó ta chia cả tử và mẫu của phân thức bên trái cho 1 – x thì thu được phân thức bên phải.)
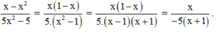
Vậy đa thức cần điền là -5x – 5.

Áp dụng quy tắc đổi dấu ta có:
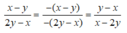
Vậy đa thức cần điền là x – 2y
Chọn đáp án B

TL
3y - x
Khi nào rảnh vào kênh H-EDITOR xem vid nha!!! Thanks!

3 y - x 2 = 3 . x - y 2 = x - y . 3 x - y
(Mẫu thức của phân thức bên trái bằng mẫu thức của phân thức bên phải chia cho 3(x – y)
Do đó ta chia cả tử và mẫu của phân thức bên phải cho 3(x – y) để thu được phân thức bên trái)
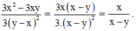
Vậy đa thức cần điền là x.

Gọi \(P\) là đa thức cần tìm.
Ta có:
\(\frac{x^5-1}{x^2-1}=\frac{\left(x-1\right)\left(x^4+x^3+x^2+x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{x^4+x^3+x^2+x+1}{x+1}\)
Vậy, \(P=x^4+x^3+x^2+x+1\)
\(\frac{x}{x+3}=\frac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{x^2-3x}{x^2-9}\)
VẬy ta điền x^2 - 3x vào chỗ ....
Đặt chỗ trống cần tìm là a
Ta có : \(\frac{a}{x^2-9}=\frac{x}{x+3}\Leftrightarrow\frac{a}{\left(x-3\right)\left(x+3\right)}=\frac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}\)
Khử mẫu : \(a=x\left(x-3\right)=x^2-3x\)
Vậy chỗ trống cần tìm là x^2 - 3x