Chứng minh hằng đẳng thức: (x - y)(x4+x3y+x2y2+xy3+y4)=(x5--y5)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-y\right)\left(x^4+x^3y+x^2y^2+xy^3+y^4\right)=x^5-y^5\)
Ta có VT:
\(\left(x-y\right)\left(x^4+x^3y+x^2y^2+xy^3+y^4\right)\)
\(=x.x^4+x.x^3y+x.x^2y^2+x.xy^3+x.y^4-y.x^4-y.x^3y-y.x^2y^2-y.xy^3-y.y^4\)
\(=x^5+x^4y+x^3y^2+x^2y^3+xy^4-x^4y-x^3y^2-x^2y^3-xy^4-y^5\)
\(=x^5-y^5\)
VT=VP
Vậy:...

Thực hiện phép nhân đa thức với đa thức ở vế trái
=> VT = VP (đpcm)

a) (x-y)(x4+x3y+x2y2+xy3+y4) = x(x4+x3y+x2y2+xy3+y4)-y(x4+x3y+x2y2+xy3+y4) =(x5+x4y+x3y2+x2y2+xy4)-(x4y+x3y2+x2y2+xy4+y5) = x5+x4y+x3y2+x2y2+xy4-x4y-x3y2-x2y2-xy4-y5 =x5-y5⇒Điều cần chứng minh
Các câu b d tương tự

Ta có
x 4 – x 3 y + x 2 y 2 – x y 3 = x 4 + x 2 y 2 – ( x 3 y + x y 3 ) = x 2 ( x 2 + y 2 ) – x y ( x 2 + y 2 ) = ( x 2 + y 2 ) ( x 2 – x y ) = ( x 2 + y 2 ) x ( x – y ) N ê n ( x 4 – x 3 y + x 2 y 2 – x y 3 ) : ( x 2 + y 2 ) = ( x 2 + y 2 ) x ( x – y ) : ( x 2 + y 2 ) = x ( x – y )
Đáp án cần chọn là : B

a) Để tính giá trị của biểu thức x^4 + y^4, ta có thể sử dụng công thức Newton về tổng lũy thừa của một đa thức. Theo công thức Newton, ta có: x^4 + y^4 = (x^2 + y^2)^2 - 2x^2y^2 Từ đó, ta có thể tính giá trị của biểu thức x^4 + y^4 theo a và b: x^4 + y^4 = (a^2 - 2b)^2 - 2(a - 2b)b b) Tương tự, để tính giá trị của biểu thức x^5 + y^5, ta có thể sử dụng công thức Newton về tổng lũy thừa của một đa thức. Theo công thức Newton, ta có: x^5 + y^5 = (x + y)(x^4 - x^3y + x^2y^2 - xy^3 + y^4) Từ đó, ta có thể tính giá trị của biểu thức x^5 + y^5 theo a và b: x^5 + y^5 = (a)(a^4 - a^3b + a^2b^2 - ab^3 + b^4)

Ta có: \(M=x^4-xy^3+xy^3-y^4-1\)
\(=x^4-y^4-1\)
\(=\left(x^2-y^2\right)\left(x^2+y^2\right)-1\)
\(=\left(x+y\right)\left(x-y\right)\left(x^2+y^2\right)-1\)(1)
Thay x+y=0 vào biểu thức (1), ta được:
\(M=0-1=-1\)
Vậy: Khi x+y=0 thì M=-1
`M=x^4-xy^3+xy^3-y^4-1`
`=x(x^3+y^3)-y^3(x+y)-1`
`=x(x+y)(x^2-xy+y^2)-0-1`(do `x+y=0`)
`=0-0-1`
`=-1`


\(\text{a) x^2 + y^2 = (x+y)^2 - 2xy = a^2 - 2b}\)
\(\text{b) x^3 + y^3 = (x+y)^3 - 3xy(x+y) = a^3 - 3ab}\)
\(\text{c) x^4 + y^4 = (x^2+y^2)^2 - 2x^2y^2 = (a^2-2b)^2 - 2b^2 = a^4 - 4a^2b + 2b^2}\)
\(\text{d) x^5 + y^5 = (x^3+y^3)(x^2+y^2) - x^2y^2(x+y) = a^5 - 5a^3b + 5ab^2}\)
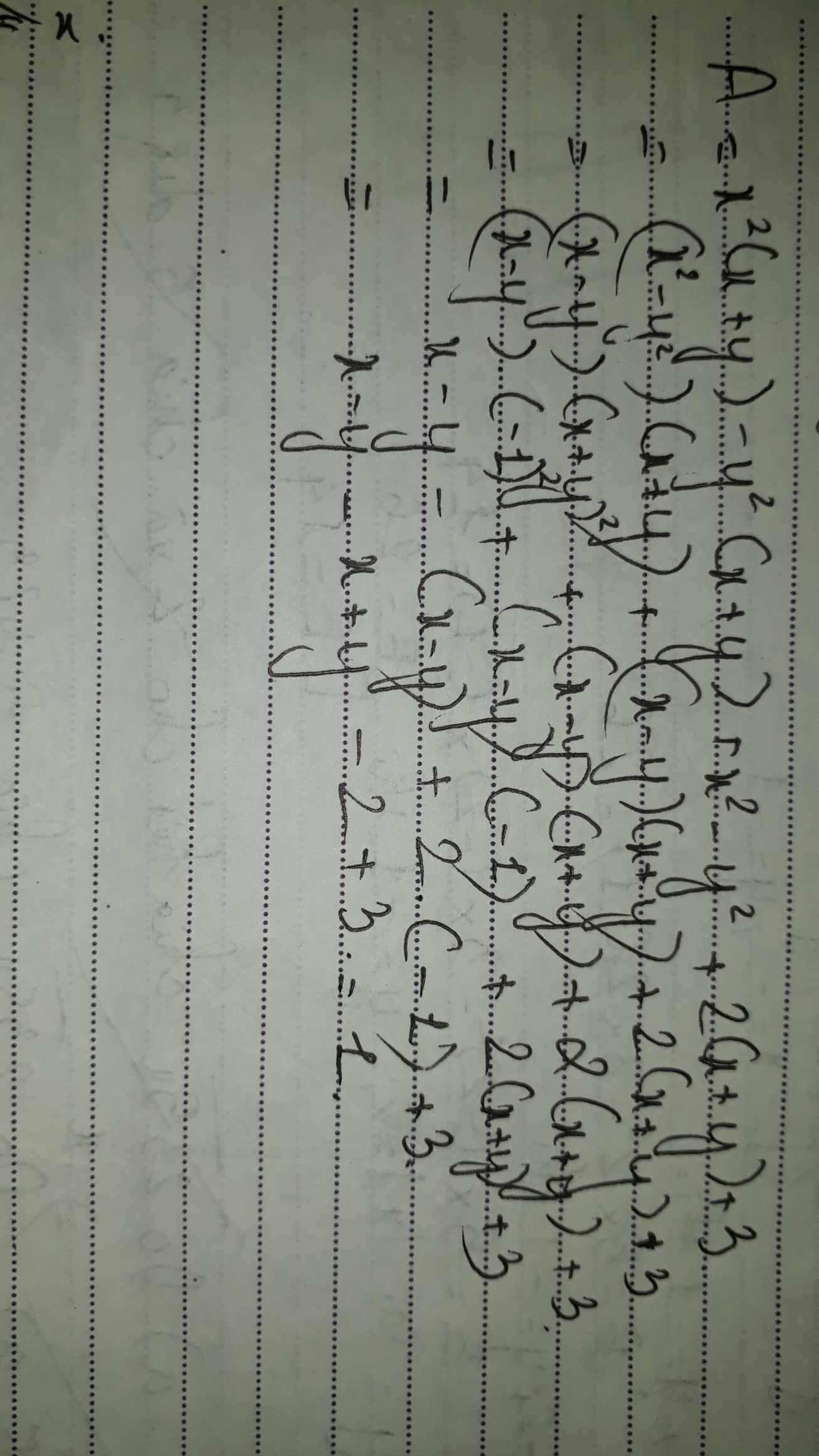
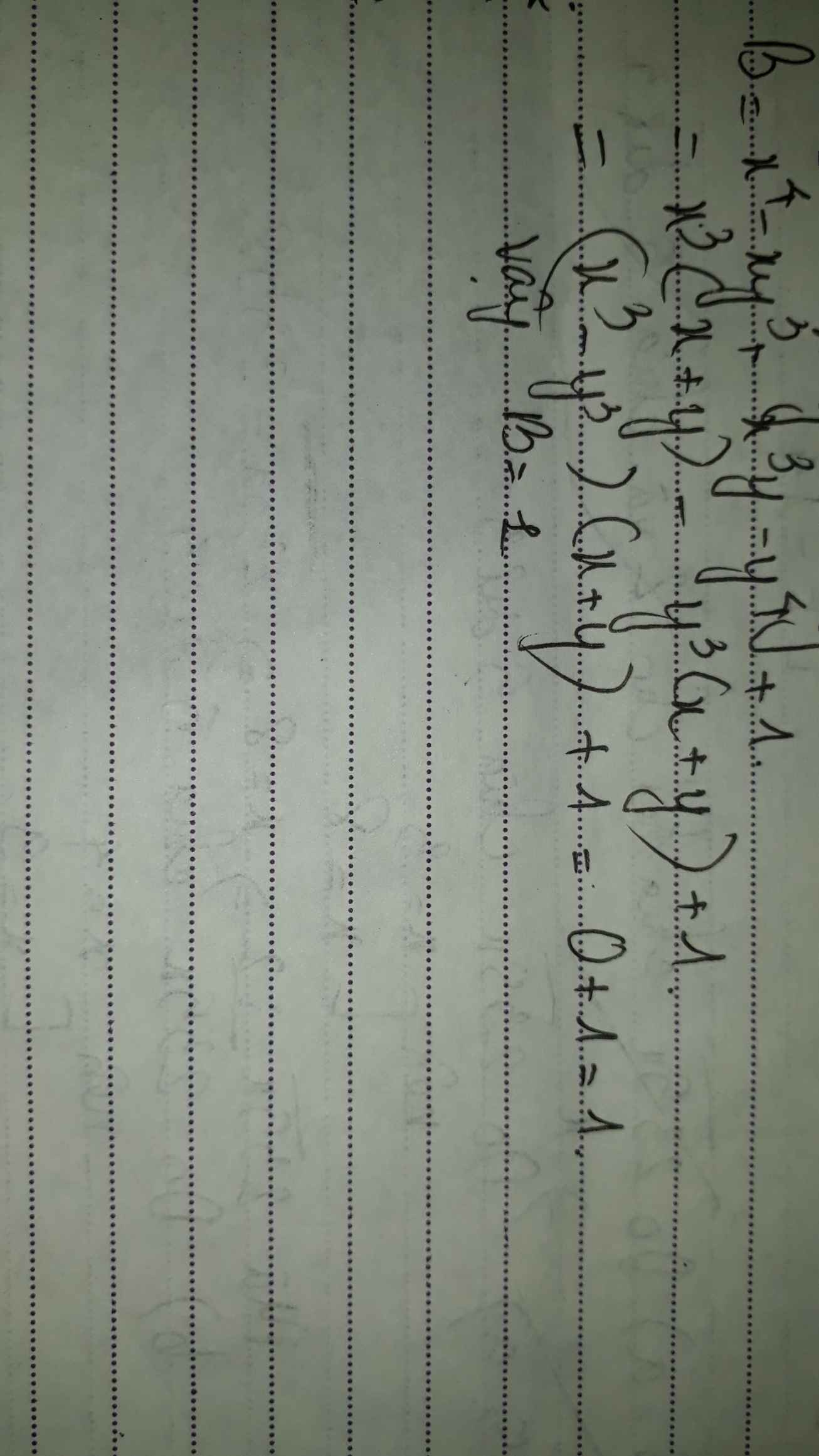
Sửa đề :Chứng minh hằng đẳng thức: ( x - y ) ( x4 + x3y + x2y2 + xy3 + y4 ) = x5 - y5
Ta có : ( x - y ) ( x4 + x3y + x2y2 + xy3 + y4 )
= x ( x4 + x3y + x2y2 + xy3 + y4 ) - y ( x4 + x3y + x2y2 + xy3 + y4 )
= x5 + x4y + x3y2 + x2y3 + xy4 - x4y - x3y2 - x2y3 - xy4 - y5
= x5 - y5
\(\implies\) ( x - y ) ( x4 + x3y + x2y2 + xy3 + y4 ) = x5 - y5 ( đpcm )
ta có : ( x - y ) ( x4 + x3y + x2y2 +xy3+ y4 )
= x ( x4 + x3y + x2y2 + xy3 + y4 ) - y ( x4 + x3y + x2y2 + xy3 + y4 )
= x5 + x4y + x3y2 + x2y3 + xy4 - x4y - x2y3 = xy4 - y5
= x5 - y5
=> ( x - y ) ( x4 + x3y + x2y2 + xy3 + y4 ) = x5 - y5 ( đpcm )
đề hơi sai nha bạn