Tính giá trị của biểu thức
\(E=cos^273+cos^247+cos73.cos47\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(B = \left( {\cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9}} \right) + \cos \frac{{11\pi }}{9} = \left( {2\cos \frac{{\frac{\pi }{9} + \frac{{5\pi }}{9}}}{2}\cos \frac{{\frac{\pi }{9} - \frac{{5\pi }}{9}}}{2}} \right) + \cos \frac{{11\pi }}{9} = 2\cos \frac{\pi }{3}\cos \frac{{2\pi }}{9} + \cos \frac{{11\pi }}{9}\)
\( = \cos \frac{{2\pi }}{9} + \cos \frac{{11\pi }}{9} = 2\cos \frac{{\frac{{2\pi }}{9} + \frac{{11\pi }}{9}}}{2}\cos \frac{{\frac{{2\pi }}{9} - \frac{{11\pi }}{9}}}{2} = 2\cos \frac{{13\pi }}{{18}}\cos \frac{\pi }{2} = 0\)

\(A.sin\dfrac{\pi}{7}=sin\left(\dfrac{\pi}{7}\right)cos\left(\dfrac{\pi}{7}\right)cos\left(\dfrac{2\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)\)
\(=\dfrac{1}{2}sin\left(\dfrac{2\pi}{7}\right)cos\left(\dfrac{2\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)\)
\(=\dfrac{1}{4}sin\left(\dfrac{4\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)\)
\(=\dfrac{1}{8}sin\left(\dfrac{8\pi}{7}\right)\)
\(=\dfrac{1}{8}sin\left(\pi+\dfrac{\pi}{7}\right)=\dfrac{1}{8}sin\left(-\dfrac{\pi}{7}\right)\)
\(=-\dfrac{1}{8}sin\left(\dfrac{\pi}{7}\right)\)
\(\Rightarrow A=-\dfrac{1}{8}\)

Chọn D.
Ta có : sin2a = 2.sina. cosa và sin2a = 1 - cos2a.
Do đó;
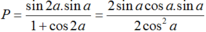
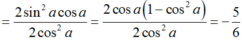

Sửa đề
\(A=cos^212+cos^223+cos^234+cos^245+cos^256+cos^267+\)
\(=\left(cos^212+cos^278\right)+\left(cos^223+cos^267\right)+\left(cos^234+cos^256\right)+cos^245\)
\(=\left(cos^212+sin^212\right)+\left(cos^223+sin^223\right)+\left(cos^234+sin^234\right)+cos^245\)
\(=1+1+1+\frac{\sqrt{2}}{2}=\frac{6+\sqrt{2}}{2}\)

\(P.sin\left(\dfrac{\pi}{7}\right)=sin\dfrac{\pi}{7}.cos\dfrac{\pi}{7}.cos\dfrac{2\pi}{7}.cos\dfrac{4\pi}{7}\)
\(\Leftrightarrow P.sin\dfrac{\pi}{7}=\dfrac{1}{2}sin\dfrac{2\pi}{7}cos\dfrac{2\pi}{7}cos\dfrac{4\pi}{7}\)
\(\Leftrightarrow P.sin\dfrac{\pi}{7}=\dfrac{1}{4}sin\dfrac{4\pi}{7}cos\dfrac{4\pi}{7}\)
\(\Leftrightarrow P.sin\dfrac{\pi}{7}=\dfrac{1}{8}sin\dfrac{8\pi}{7}=\dfrac{1}{8}sin\left(\pi+\dfrac{\pi}{7}\right)\)
\(\Leftrightarrow P.sin\dfrac{\pi}{7}=-\dfrac{1}{8}sin\dfrac{\pi}{7}\)
\(\Rightarrow P=-\dfrac{1}{8}\)

\(A = \cos {75^0}\cos {15^0} = \frac{1}{2}\left[ {\cos \left( {{{75}^0} - {{15}^0}} \right) + \cos \left( {{{75}^0} + {{15}^0}} \right)} \right] \\= \frac{1}{2}.\cos {60^0}.\cos {90^0} = 0\)
\(B = \sin \frac{{5\pi }}{{12}}\cos \frac{{7\pi }}{{12}} = \frac{1}{2}\left[ {\sin \left( {\frac{{5\pi }}{{12}} - \frac{{7\pi }}{{12}}} \right) + \sin \left( {\frac{{5\pi }}{{12}} + \frac{{7\pi }}{{12}}} \right)} \right] \\= \frac{1}{2}\sin \left( { - \frac{{2\pi }}{{12}}} \right).\sin \left( {\frac{{12\pi }}{{12}}} \right) = - \frac{1}{2}\sin \frac{\pi }{6}\sin \pi = 0\)
\(E=\)\(cos^273+1-sin^247+cos73\left(cos120.cos73+sin120.sin73\right)\)
\(=cos^273+1-\left(sin120.cos73-cos120.sin73\right)^2-\dfrac{1}{2}.cos^273+\dfrac{\sqrt{3}}{2}cos73.sin73\)
\(=cos^273+1-\left(\dfrac{\sqrt{3}}{2}.cos73+\dfrac{1}{2}.sin73\right)^2-\dfrac{1}{2}.cos73^2+\dfrac{\sqrt{3}}{2}cos73.sin73\)
\(=\dfrac{1}{2}cos^273+1-\left(\dfrac{3}{4}cos^273+\dfrac{\sqrt{3}}{2}.cos73.sin73+\dfrac{1}{4}sin^273\right)+\dfrac{\sqrt{3}}{2}.cos73.sin73\)
\(=1-\dfrac{1}{4}.cos^273-\dfrac{1}{4}.sin^273\)
\(=1-\dfrac{1}{4}=\dfrac{3}{4}\)
Đề có sai không bạn nhỉ?