Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải
c) Gọi đường tròn tâm O tiếp xúc với AB có bán kính R.
Gọi H, K là chân đường vuông góc hạ từ O đến DE và AB.
⇒ R = OK.
O ∈ đường phân giác của 
⇒ OH = OK.
⇒ OH = R
⇒ DE tiếp xúc với (O; R) (đpcm).
Lời giải
c) Gọi đường tròn tâm O tiếp xúc với AB có bán kính R.
Gọi H, K là chân đường vuông góc hạ từ O đến DE và AB.
⇒ R = OK.
O ∈ đường phân giác của 
⇒ OH = OK.
⇒ OH = R
⇒ DE tiếp xúc với (O; R) (đpcm).
\(OB^2=BD.CE\Rightarrow OB.OB=BD.CE\Rightarrow\frac{OB}{BD}=\frac{CE}{0B}\)MÀ 0B= 0B
\(\Rightarrow\frac{OB}{BD}=\frac{CE}{0C}\Rightarrow\frac{OB}{CE}=\frac{BD}{OC}\)
xét tam giác BDO và tam giác COE
CÓ \(\frac{OB}{CE}=\frac{BD}{OC}\) ( CMT )
góc DBO = góc ECO ( tam giác cân )
=> tam giác BDO đoòng dạng với tam giác COE ( trường hợp 2 c-g-c)
b)
có tam giác BDO đồng dạng với tam giác COE (cmt ) => bdo =oec mà dbo = eco => dob = eoc (1)
cm doe = dob
* : bài mk có thể sai và chưa chính xác vì vậy xin m.n đừng cmt ns lung tung ,ko hiểu thì hỏi ,sai thì ib chỉ hộ mk ,mk chỉ làm bt chứ ko phải vì kiếm 'k' vì vì thê mấy thể loại xx jj đó xin đừng quan tâm ,
thanks nhé ,có thể sai lên mk ko chắc,sai chỗ nào xin chỉ giúp mk để mk pít mà sửa ak ,thanks
a, Theo đề bài ta có: BO^2 = BD.CE => BO.BO = BD. CE mà BO=CO (O là trung điểm BC)
=>BO.CO=BD.CE => \(\frac{BO}{CE}=\frac{BD}{CO}\)
Xét tam giác BDO và tam giác COE có:
góc B = góc C (tam giác ABC cân tại A)
\(\frac{BO}{CE}=\frac{BD}{CO}\)(c.m.t)
=> tam giác BDO đồng dạng với tam giác COE (c.g.c) (đpcm)
H là gì , ở đâu đấy bn?
bn xem lại đề đi nhé
có j mk giúp
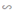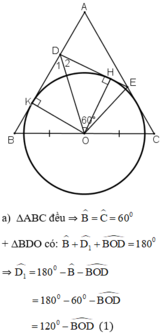
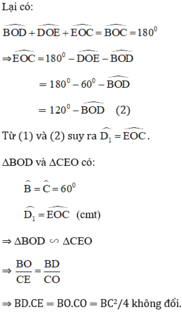
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
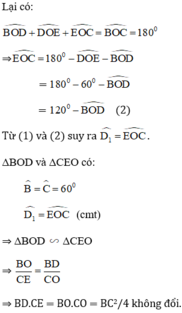
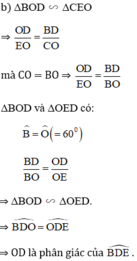
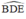
a, ^BOD + ^OBD = 120 = ^BOD + ^EOC (vì ^DOE = 60)
=> ^BDO = ^EOC
=> ∆BDO đồng dạng ∆COE
=> BD/BO = CO/CE
<=> BD.CE = BC²/4
b, DO/OE = BD/CO
<=> BO/OE = BD/OD
=> ∆BOD đồng dạng ∆OED
=> ^BDO = ^ODE
=> OD là tia phân giác của góc BDE
c, kẻ OI,OK lần lượt vuông góc với AB,DE
AB tiếp xúc với (O;OI)
có ∆IOD = ∆KOD (cạnh huyền góc nhọn)
=> OI = OK
mà OK ┴ DE
=> (O) luôn tiếp xúc với DE
a) \(\Delta ABC\Rightarrow\widehat{B}=\widehat{C}=60^o\)
+) \(\Delta BDO\)có : \(\widehat{B}+\widehat{D_1}+\widehat{BOD}=180^o\)
\(\Rightarrow\widehat{D_1}=180^o-\widehat{B}-\widehat{BOD}\)
\(=180^o-60^o-\widehat{BOD}\)
\(=120^o-\widehat{BOD}\left(1\right)\)
Ta lại có :
\(\widehat{BOD}+\widehat{DOE}+\widehat{EOC}=\widehat{BOC}=180^o\)
\(\Rightarrow\widehat{EOC}=180^o-\widehat{DOE}-\widehat{BOD}\)
\(=180^o-60^o-\widehat{BOD}\)
\(=120^o-\widehat{BOD}\left(2\right)\)
Từ (1) và (2) , suy ra : \(\widehat{D_1}=\widehat{EOC}\)
\(\Delta BOD\)và \(\Delta EOC\)có :
\(\widehat{B}=\widehat{C}=60^o\)
\(\widehat{D_1}=\widehat{EOC}\left(cmt\right)\)
\(\Rightarrow\Delta BOD~\Delta EOC\)
\(\Rightarrow\frac{BO}{CE}=\frac{BD}{CO}\)
\(\Rightarrow BD.CE=BO.CO=\frac{BC^2}{4}\)
b) \(\Delta BOD~\Delta EOC\)
\(\Rightarrow\frac{OD}{EO}=\frac{BD}{CO}\)
mà CO = BO \(\Rightarrow\frac{OD}{EO}=\frac{BD}{BO}\)
\(\Delta BOD\)và \(\Delta OED\)có :
\(\widehat{B}=\widehat{O}\left(=60^o\right)\)
\(\frac{BD}{BO}=\frac{OD}{OE}\)
\(\Rightarrow\Delta BOD~\Delta OED\)
\(\Rightarrow\widehat{BDO}=\widehat{ODE}\)
=> OD là tia phân giác của góc BDE
c) Gọi đường tròn tâm O tiếp xúc với AB có bán kính R
Gọi H, K là chân đường vuông góc hạ từ O đến DE và AB
=> R = OK
O thuộc đường phân giác của \(\widehat{BDE}\)
=> OH = OK.
=> OH = R
=> DE tiếp xúc với ( O ; R ) (đpcm)