với giá trị nào của m , thì hàm số y=(m2-5m+6)x2+(m2+mn-6n2)x+3 là hàm số bậc nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
5 tháng 11 2023
a) Để hàm số đã cho là hàm số bậc nhất thì:
3m + 5 ≠ 0
⇔ 3m ≠ -5
⇔ m ≠ -5/3
b) Để hàm số đã cho là hàm số bậc nhất thì:
2m² + 3 ≠ 0
⇔2m² ≠ -3 (luôn đúng)
Vậy m ∈ R
c) Để hàm số đã cho là hàm số bậc nhất thì:
m² - 3m = 0 và 3 - m ≠ 0
*) m² - 3m = 0
⇔ m(m - 3) = 0
⇔ m = 0 hoặc m - 3 = 0
**) m - 3 = 0
⇔ m = 3
*) 3 - m ≠ 0
⇔ m ≠ 3
Vậy m = 0 thì hàm số đã cho là hàm số bậc nhất
5 tháng 11 2023
a: Để đây là hàm số bậc nhất thì 3m+5<>0
=>3m<>-5
=>\(m< >-\dfrac{5}{3}\)
b: Để đây là hàm số bậc nhất thì \(2m^2+3\ne0\)
mà \(2m^2+3>=3>0\forall m\)
nên \(m\in R\)
c: Để đây là hàm số bậc nhất thì \(\left\{{}\begin{matrix}m^2-3m=0\\3-m< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-3\right)=0\\m< >3\end{matrix}\right.\Leftrightarrow m=0\)
CM
20 tháng 4 2017
Hàm số y = ( m 2 – 9 m + 8 ) x + 10 là hàm số bậc nhất khi m 2 – 9 m + 8 ≠ 0
( m – 1 ) ( m – 8 ) ≠ 0 ⇔ m − 1 ≠ 0 m − 8 ≠ 0 ⇔ m ≠ 1 m ≠ 8
Đáp án cần chọn là: A
CM
22 tháng 6 2018
Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
y′(1) = –3
m
2
– 3m + 6 = 0 ⇔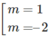 
Mặt khác, y” = –6( m 2 + 5m)x + 12m
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 8 2021
Hàm là bậc nhất khi:
a. \(3m-2\ne0\Rightarrow m\ne\dfrac{2}{3}\)
b. \(3-m>0\Rightarrow m< 3\)
c. \(\left\{{}\begin{matrix}2m-1\ne0\\m+2\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\m\ne-2\end{matrix}\right.\)
d. \(\left\{{}\begin{matrix}m^2-4=0\\m+2\ne0\end{matrix}\right.\) \(\Rightarrow m=2\)
17 tháng 8 2021
a: ĐKXĐ: \(m\ne\dfrac{2}{3}\)
b: ĐKXĐ: \(m< 3\)
c: ĐKXĐ: \(\left[{}\begin{matrix}m\ge\dfrac{1}{2}\\m< -2\end{matrix}\right.\)
d: ĐKXĐ: \(m=2\)
15 tháng 1 2022
a: ĐKXĐ: m<>1
b: ĐKXĐ: \(m^2-2m-3-m-1< >0\)
=>(m-4)(m+1)<>0
hay \(m\notin\left\{4;-1\right\}\)
CM
13 tháng 12 2017
a) y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+) m2 + 5m = 0 ⇔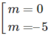 
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
Δ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
b) Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
y′(1) = –3
m
2
– 3m + 6 = 0 ⇔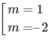 
Mặt khác, y” = –6( m 2 + 5m)x + 12m
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.
TM
18 tháng 2 2021
câu a và b thay số vào là ra nhé, bài mik hơi khác:
Ta có m^2 + 2m + 3 = m^2 + 2m + 1 + 2 = (m + 1)^2 + 2 > 0 với mọi m.
Suy ra hàm số đã cho đồng biến với mọi m với x > 0 và nghịch biến với x < 0
18 tháng 2 2021
a) Vì \(m^2+2m+5>0\forall m\) nên để hàm số \(y=\left(m^2+2m+5\right)x^2\) đồng biến thì x>0
b) Vì \(m^2+2m+5>0\forall m\) nên để hàm số \(y=\left(m^2+2m+5\right)x^2\) nghịch biến thì x<0
c) Thay x=1 và y=8 vào hàm số \(y=\left(m^2+2m+5\right)x^2\), ta được:
\(m^2+2m+5=8\)
\(\Leftrightarrow m^2+2m-3=0\)
\(\Leftrightarrow m^2+3m-m-3=0\)
\(\Leftrightarrow m\left(m+3\right)-\left(m+3\right)=0\)
\(\Leftrightarrow\left(m+3\right)\left(m-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m+3=0\\m-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-3\\m=1\end{matrix}\right.\)