Cho △ABC có góc B và góc C là góc nhọn, AH ⊥ BC tại H. Các khẳng định nào sau đây là sai?
A. AH < AB, AH < AC
B. HB < AB, HC < AC
C. Nếu góc HBA < góc HCA thì HB < HC
D. Nếu AB < AC thì góc HAB < góc HAC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có AC>AB
nên góc B>góc C
b: Xét ΔABC có AB<AC
mà HB,HC lần lượt là hình chiếu của AB,AC trên BC
nên HB<HC
c: góc B+góc C=90 độ
góc HAC+góc C=90 độ
=>góc B=góc HAC
góc C+góc B=90 độ
góc HAB+góc B=90 độ
=>góc C=góc HAB

Ta có: \(\widehat{HAB}+\widehat{B}=90^0\)(ΔHAB vuông tại H)
\(\widehat{HAC}+\widehat{C}=90^0\)(ΔHAC vuông tại H)
mà \(\widehat{HAB}< \widehat{HAC}\)
nên \(\widehat{B}>\widehat{C}\)
Xét ΔABC có \(\widehat{B}>\widehat{C}\)
mà AC,AB lần lượt là cạnh đối diện của các góc ABC và góc ACB
nên AC>AB
Xét ΔABC có
AB<AC
HB,HC lần lượt là hình chiếu của AB,AC trên BC
Do đó: HB<HC

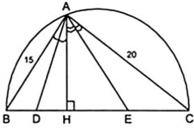
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A, ta được:
B C 2 = A C + A B 2 ⇒ B C 2 = 15 2 + 20 2 ⇔ B C 2 = 25 2 ⇔ BC = 25( cm )
Đặt BD = x ⇒ DC = 25 - x
Áp dụng định lý Py 0 ta – go vào hai tam giác vuông AHB và AHC, ta được:
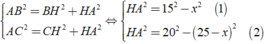
Trừ theo vế các đẳng thức ( 1 ) và ( 2 ) ta được:
15 2 - x 2 - 20 2 + ( 25 - x ) 2 = 0 ⇔ 50x = 450 ⇔ x = 9( cm )
Nên HC = 25 - 9 = 16( cm )
Thay x = 9 vào đẳng thức ( 1 ) ta có: H A 2 = 15 2 - 9 2 = 122 ⇔ HA = 12( cm )
Áp dụng tính chất đường phân giác AD vào tam giác AHB, ta được:
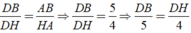
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
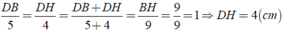
Áp dụng tính chất đường chất đường phân giác AE của tam giác ACH, ta được:
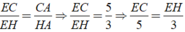
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
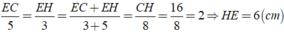

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
b: BH=CH=BC/2=4(cm)
nên AH=3(cm)
c: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
\(\widehat{EAH}=\widehat{DAH}\)
DO đó: ΔAEH=ΔADH
Suy ra: HE=HD
hay ΔHDE cân tại H

Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm
Chọn D