 cíu lẹ ạ!
cíu lẹ ạ!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề bài không rõ ràng, em liên hệ người ra đề xem vẽ đồ thị đường thẳng nào? Vì đường thẳng đề cho có a chưa biết




a. Ta có: $\sin x\in [-1;1]$ nên $|\sin x|\in [0;1]$
$\Rightarrow 1\leq 3-2|\sin x|\leq 3$
Vậy $y_{\min}=1; y_{\max}=3$
b.
$y=\frac{1-\cos 2x}{2}-\frac{3}{2}\sin 2x+1$
$2y=3-\cos 2x-3\sin 2x$
$3-2y=\cos 2x+3\sin x$
Áp dụng định lý Bunhiacopxky:
$(3-2y)^2\leq (\cos ^22x+\sin ^22x)(1+3^2)=10$
$\Rightarrow -\sqrt{10}\leq 3-2y\leq \sqrt{10}$
$\Rightarrow \frac{3-\sqrt{10}}{2}\leq y\leq \frac{3+\sqrt{10}}{2}$
Vậy $y_{\max}=\frac{1+\sqrt{10}}{2}; y_{\min}=\frac{1-\sqrt{10}}{2}$
c.
\(y=\sqrt{5-\frac{1}{4}(2\sin x\cos x)^2}=\sqrt{5-\frac{1}{2}\sin ^22x}\)
Vì $\sin 2x\in [-1;1]$
$\Rightarrow \sin ^22x\in [0;1]$
$\Rightarrow \frac{3\sqrt{2}}{2}\leq \sqrt{5-\frac{1}{2}\sin ^22x}\leq \sqrt{5}$
d.
$\cos (x+\frac{\pi}{3})\in [-1;1]$
$\Rightarrow 2(-1)+3\leq 2\cos (x+\frac{\pi}{3})+3\leq 2.1+3$
$\Rightarrow 1\leq y\leq 5$
$\Rightarrow y_{\min}=1; y_{\max}=5$

 cíu lẹ cíu lẹ
cíu lẹ cíu lẹ 







 Cíu em với ạ:
Cíu em với ạ:
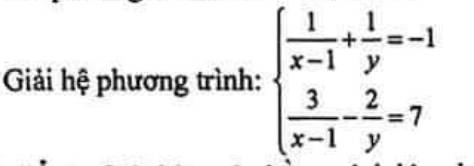
ĐKXĐ: x<>1 và y<>0
\(\left\{{}\begin{matrix}\dfrac{1}{x-1}+\dfrac{1}{y}=-1\\\dfrac{3}{x-1}-\dfrac{2}{y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{x-1}+\dfrac{2}{y}=-2\\\dfrac{3}{x-1}-\dfrac{2}{y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x-1}=5\\\dfrac{1}{x-1}+\dfrac{1}{y}=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-1=1\\\dfrac{1}{y}=-1-1=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\dfrac{1}{2}\end{matrix}\right.\left(nhận\right)\)