9.2
cho `x^2 -4x+m-5=0`
tìm m để pt có 2 nghiệm pb `x_1 ;x_2` thỏa mãn \(\left(x_1-1\right)\left(x_2^2-3x_2+m-6\right)=-3\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

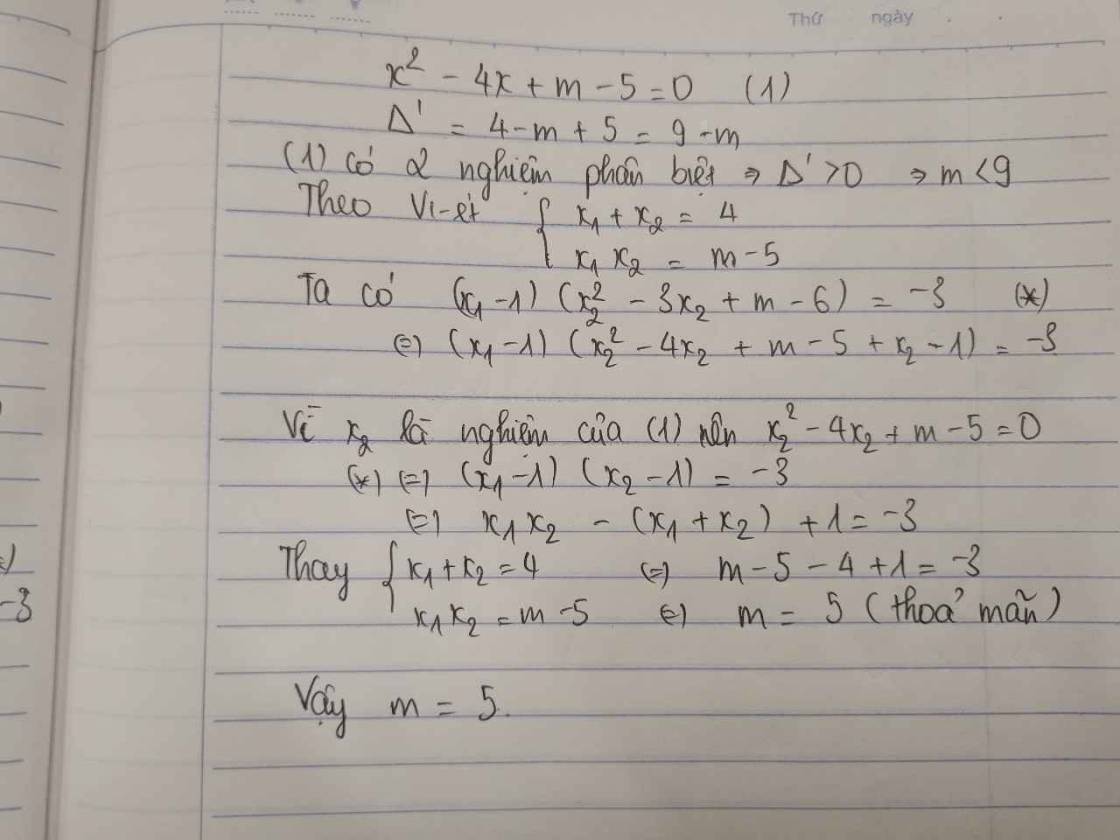

\(a+b+c=1-\left(2m+1\right)+2m=0\)
\(\Rightarrow\) Phương trình có 2 nghiệm \(x=1\) ; \(x=2m\)
Để pt có 2 nghiệm pb \(\Rightarrow2m\ne1\Rightarrow m\ne\dfrac{1}{2}\)
\(\left|x_1^2-x_2^2\right|=35\)
\(\Leftrightarrow\left|4m^2-1\right|=35\)
\(\Leftrightarrow\left[{}\begin{matrix}4m^2-1=35\\4m^2-1=-35\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2=9\\m^2=-\dfrac{17}{2}\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=3\\m=-3< 0\left(loại\right)\end{matrix}\right.\)

Để phương trình có hai nghiệm phân biệt thỏa mãn \(x_1< 0\le x_2\) thì \(1\left(m-4\right)< 0\)
\(\Leftrightarrow m-4< 0\)
hay m<4

a) \(\Delta\)=(m-3)2-4.1.(2m-11)=m2-14m+53=(m-7)2+4\(\ge\)4.
\(\Rightarrow\) Phương trình đã cho luôn có hai nghiệm phân biệt với mọi m.
b) Từ ycđb, ta có: x12+x22=42 \(\Leftrightarrow\) (x1+x2)2-2x1x2=16 \(\Leftrightarrow\) (m-3)2-2(2m-11)=16 \(\Leftrightarrow\) m2-10m+15=0 \(\Leftrightarrow\) \(m=5\pm\sqrt{10}\).

Ta có \(\Delta=\left(m+2\right)^2-4\left(m+8\right)>0\)
<=> \(m^2-28>0\)
<=> \(\orbr{\begin{cases}m>\sqrt{28}\\m< -\sqrt{28}\end{cases}}\)
Áp dụng hệ thức vi-et ta có
\(\hept{\begin{cases}x_1+x_2=m+2\\x_1x_2=m+8\end{cases}}\)
=> \(x_1+x_2-x_1x_2+6=0\)
Mà \(x_1^3=x_2\)
=> \(x_1^3+x_1-x_1^4+6=0\)
<=> \(\)\(x_1=2\)
=> m=8(thỏa mãn ĐK)
Vậy m=8

Lời giải:
Để pt có 2 nghiệm thì: $\Delta=25-4(m-2)\geq 0$
$\Leftrightarrow m\leq \frac{33}{4}$
Áp dụng hệ thức Viet, với $x_1,x_2$ là 2 nghiệm của pt thì:
$x_1+x_2=-5$
$x_1x_2=m-2$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=2$
$\Leftrightarrow \frac{x_1+x_2-2}{(x_1-1)(x_2-1)}=2$
$\Leftrightarrow \frac{-5-2}{(x_1-1)(x_2-1)}=2$
$\Leftrightarrow (x_1-1)(x_2-1)=\frac{-7}{2}$
$\Leftrightarrow x_1x_2-(x_1+x_2)+1=\frac{-7}{2}$
$\Leftrightarrow m-2+5+1=\frac{-7}{2}$
$\Leftrightarrow m=\frac{-15}{2}$ (tm)
Lời giải:
Để pt có 2 nghiệm thì: $\Delta=25-4(m-2)\geq 0$
$\Leftrightarrow m\leq \frac{33}{4}$
Áp dụng hệ thức Viet, với $x_1,x_2$ là 2 nghiệm của pt thì:
$x_1+x_2=-5$
$x_1x_2=m-2$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=2$
$\Leftrightarrow \frac{x_1+x_2-2}{(x_1-1)(x_2-1)}=2$
$\Leftrightarrow \frac{-5-2}{(x_1-1)(x_2-1)}=2$
$\Leftrightarrow (x_1-1)(x_2-1)=\frac{-7}{2}$
$\Leftrightarrow x_1x_2-(x_1+x_2)+1=\frac{-7}{2}$
$\Leftrightarrow m-2+5+1=\frac{-7}{2}$
$\Leftrightarrow m=\frac{-15}{2}$ (tm)

a: Thay m=4 vào phương trình, ta được:
\(x^2-4x+4-1=0\)
=>\(x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
b: \(\text{Δ}=\left(-4\right)^2-4\cdot1\left(m-1\right)\)
\(=16-4m+4=-4m+20\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>-4m+20>0
=>-4m>-20
=>\(m< 5\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{\left(-4\right)}{1}=4\\x_1\cdot x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
\(x_1\left(x_1+2\right)+x_2\left(x_2+2\right)=20\)
=>\(\left(x_1^2+x_2^2\right)+2\left(x_1+x_2\right)=20\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=20\)
=>\(4^2-2\cdot\left(m-1\right)+2\cdot4=20\)
=>-2(m-1)+24=20
=>-2(m-1)=-4
=>m-1=2
=>m=3(nhận)

`1)`
$a\big)\Delta=7^2-5.4.1=29>0\to$ PT có 2 nghiệm pb
$b\big)$
Theo Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{7}{5}\\x_1x_2=\dfrac{1}{5}\end{matrix}\right.\)
\(A=\left(x_1-\dfrac{7}{5}\right)x_1+\dfrac{1}{25x_2^2}+x_2^2\\ \Rightarrow A=\left(x_1-x_1-x_2\right)x_1+\left(\dfrac{1}{5}\right)^2\cdot\dfrac{1}{x_2^2}+x_2^2\\ \Rightarrow A=-x_1x_2+\left(x_1x_2\right)^2\cdot\dfrac{1}{x_2^2}+x_2^2\)
\(\Rightarrow A=-x_1x_2+x_1^2+x_2^2\\ \Rightarrow A=\left(x_1+x_2\right)^2-3x_1x_2\\ \Rightarrow A=\left(\dfrac{7}{5}\right)^2-3\cdot\dfrac{1}{5}=\dfrac{34}{25}\)

a.\(\Delta=\left(-4\right)^2-4.\left(1-2m\right)\)
\(=16-4+8m=12+8m\)
Để pt có 2 nghiệm thì \(12+8m>0\)
\(\Leftrightarrow m>-\dfrac{12}{8}\)
b. Theo hệ thức vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1.x_2=1-2m\end{matrix}\right.\)
\(x_1^2+x^2_2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow4^2-2\left(1-2m\right)=6\)
\(\Leftrightarrow16-2+4m-6=0\)
\(\Leftrightarrow4m=-8\)
\(\Leftrightarrow m=-2\)
a, \(\Delta'=\left(-2\right)^2-\left(1-2m\right)=4-1+2m=2m-3\)
Để pt có nghiệm thì \(\Delta'\ge0\Leftrightarrow2m-3\ge0\Leftrightarrow m\ge\dfrac{3}{2}\)
b, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=1-2m\end{matrix}\right.\)
\(x_1^2+x_2^2=6\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\\ \Leftrightarrow4^2-2\left(1-2m\right)=6\\ \Leftrightarrow16-2+4m-6=0\\ \Leftrightarrow4m-8=0\\ \Leftrightarrow m=2\left(tm\right)\)