Mong mn giúp mình ! Mình cảm ơn trước ạ:<
Làm theo cách của lớp 9,giải theo cách cơ bản
K
Khách
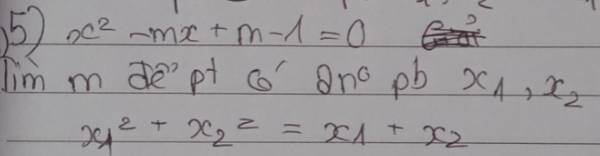
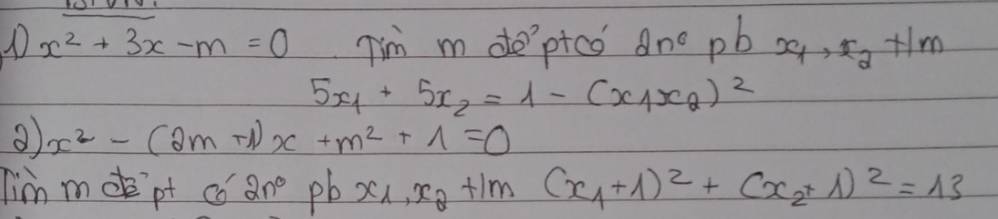
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
1
9 tháng 11 2023
a: ΔAMN vuông tại A
mà AI là đường trung tuyến
nên AI=IM=IN=MN/2
=>I là tâm đường tròn ngoại tiếp ΔAMN
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
LT
1
11 tháng 11 2023
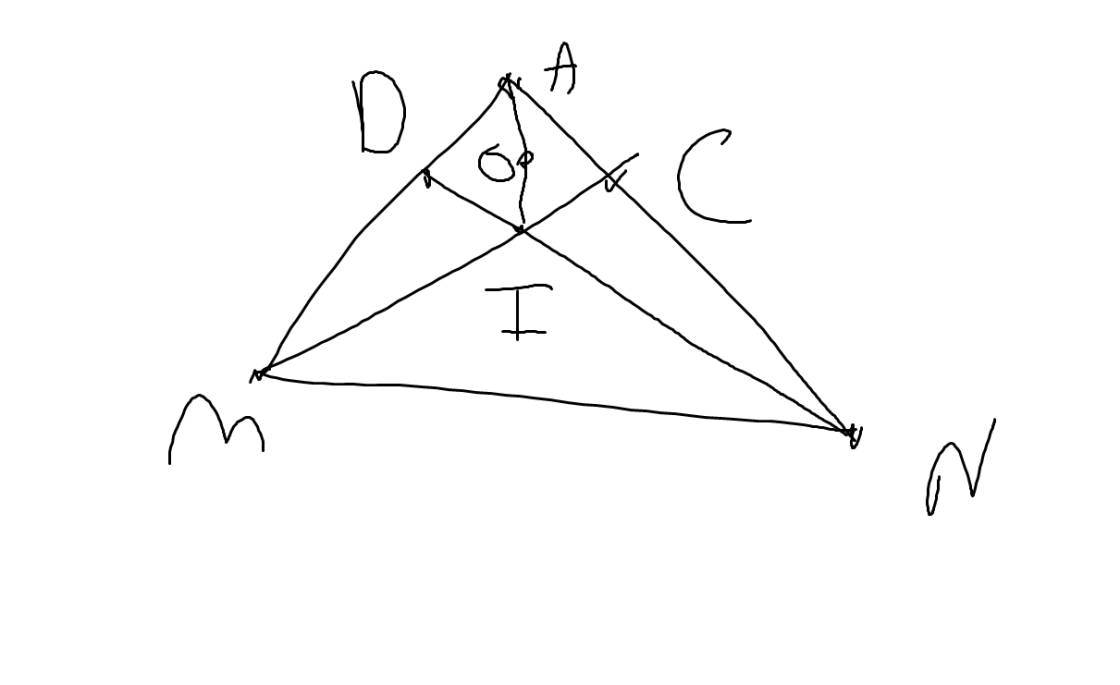
a: Sửa đề: Hai đường cao MC và ND cắt nhau tại I
Xét tứ giác MDCN có \(\widehat{MDN}=\widehat{MCN}=90^0\)
nên MDCN là tứ giác nội tiếp
=>M,D,C,N cùng thuộc một đường tròn
b: Xét tứ giác ADIC có
\(\widehat{ADI}+\widehat{ACI}=90^0+90^0=180^0\)
=>ADIC là tứ giác nội tiếp đường tròn đường kính AI
=>A,D,I,C cùng thuộc đường tròn đường kính AI
Tâm O là trung điểm của AI
DT
1
28 tháng 1 2024
\(\dfrac{S_{AOD}}{S_{DOC}}=\dfrac{10}{20}=\dfrac{1}{2}\)
=>\(AO=\dfrac{1}{2}CO\)
Vì ABCD là hình thang có hai đáy là AB và CD
và AC cắt BD tại O
nên \(S_{AOD}=S_{BOC}\)
=>\(S_{BOC}=10\left(cm^2\right)\)
\(AO=\dfrac{1}{2}OC\)
=>\(S_{AOB}=\dfrac{1}{2}\cdot S_{BOC}=5\left(cm^2\right)\)
\(S_{ABCD}=S_{ABO}+S_{BOC}+S_{DOC}+S_{AOD}\)
\(=5+10+20+10=45\left(cm^2\right)\)
DT
Giúp mình giải bài 3 theo cách của lớp 5 với ạ. Cảm ơn mọi người nhiều.
1
AH
Akai Haruma
Giáo viên
27 tháng 1 2024
Bài 3:
Nếu đáy lớn được tăng thêm 5 cm thì diện tích sẽ tăng một phần bằng 5 x chiều cao : 2
Vậy chiều cao của hình thang là:
$20\times 2:5=2$ (m)
Diện tích hình thang ban đầu là:
$50\times 2:2=50$ (m2)
LT
1
20 tháng 10 2023
a: ΔABC vuông tại B
=>\(\widehat{A}+\widehat{C}=90^0\)
=>\(\widehat{A}=50^0\)
Xét ΔBAC vuông tại B có
\(sinC=\dfrac{AB}{AC}\)
=>\(AC=\dfrac{6}{sin40}\simeq9,33\left(cm\right)\)
ΔBAC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC=\sqrt{9.33^2-6^2}\simeq7,14\left(cm\right)\)
b: ΔBAC vuông tại B có BH là đường cao
nên \(HC\cdot HA=BH^2\left(1\right)\)
ΔBHC vuông tại H có HI là đường cao
nên \(BI\cdot BC=BH^2\left(2\right)\)
Từ (1),(2) suy ra \(HC\cdot HA=BI\cdot BC\)
c: ΔBHA vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\left(3\right)\)
Từ (2),(3) suy ra \(BI\cdot BC=BM\cdot BA\)
=>\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)
Xét ΔBIM vuông tại B và ΔBAC vuông tại B có
\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)
Do đó: ΔBIM đồng dạng với ΔBAC
LT
1
20 tháng 10 2023
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: Xét ΔABC vuông tại A có AM là đường cao
nên \(\left\{{}\begin{matrix}AB\cdot AC=AM\cdot BC\\AB^2=BM\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AM=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\\BM=\dfrac{12^2}{20}=7.2\left(cm\right)\end{matrix}\right.\)
c: ΔABM vuông tại M có ME là đường cao
nên \(AE\cdot AB=AM^2\)
ΔAMC vuông tại M
=>\(MA^2+MC^2=AC^2\)
=>\(MA^2=AC^2-MC^2\)
=>\(AE\cdot AB=AC^2-MC^2\)
C
27 tháng 12 2023
\(5^{x+1}+5^{x-1}=130\)
\(5^x\cdot5^1+5^x\div5^1=130\)
\(5^x\cdot5^1+5^x\cdot\dfrac{1}{5}=130\)
\(5^x\cdot\left(5+\dfrac{1}{5}\right)=130\)
\(5^x\cdot\dfrac{26}{5}=130\)
\(5^x=130\div\dfrac{26}{5}\)
\(5^x=130\cdot\dfrac{5}{26}\)
\(5^x=25\)
\(\Rightarrow5^x=5^2\)
\(\Rightarrow x=2\)
27 tháng 12 2023
Mọi người còn câu trả lời nào khác không cứ trả lời đi mik tick cho
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2024
d.
Ta có: \(AB=AC\) (t/c hai tiếp tuyến cắt nhau)
\(OB=OC=R\)
\(\Rightarrow OA\) là trung trực BC hay OA vuông góc BC tại I
Xét hai tam giác vuông AIB và ABO có:
\(\left\{{}\begin{matrix}\widehat{AIB}=\widehat{ABO}=90^0\\\widehat{BAI}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta AIB\sim\Delta ABO\left(g.g\right)\)
\(\Rightarrow\dfrac{AI}{AB}=\dfrac{AB}{AO}\Rightarrow AI.AO=AB^2\)
Theo c/m câu c có \(AB^2=AE.AF\)
\(\Rightarrow AI.AO=AE.AF\)
e.
Từ đẳng thức trên ta suy ra: \(\dfrac{AI}{AF}=\dfrac{AE}{AO}\)
Xét hai tam giác AIE và AFO có:
\(\left\{{}\begin{matrix}\dfrac{AI}{AF}=\dfrac{AE}{AO}\left(cmt\right)\\\widehat{OAF}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta AIE\sim\Delta AFO\left(c.g.c\right)\)
\(\Rightarrow\widehat{AFO}=\widehat{AIE}\)
Mà \(\widehat{AIE}+\widehat{OIE}=180^0\) (kề bù)
\(\Rightarrow\widehat{AFO}+\widehat{OIE}=180^0\)
\(\Rightarrow\) Tứ giác FOIE nội tiếp
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2024
a.
Do AB là tiếp tuyến của (O) \(\Rightarrow AB\perp OB\Rightarrow\widehat{ABO}=90^0\)
\(\Rightarrow\) 3 điểm A, B, O thuộc đường tròn đường kính OA (1)
Tương tự AC là tiếp tuyến của (O) nên 3 điểm A, C, O thuộc đường tròn đường kính OA
\(\Rightarrow\) 4 điểm A, B, C, O thuộc đường tròn đường kính OA hay tứ giác ABOC nội tiếp
b.
Do M là trung điểm EF \(\Rightarrow OM\perp EF\Rightarrow\widehat{OMA}=90^0\)
\(\Rightarrow\) 3 điểm A, M, O thuộc đường tròn đường kính OA (2)
(1);(2) \(\Rightarrow\) 4 điểm A, B, M, O thuộc đường tròn đường kính OA
Hay tứ giác ABMO nội tiếp
c.
Xét hai tam giác ABE và AFB có:
\(\left\{{}\begin{matrix}\widehat{EAB}\text{ chung}\\\widehat{ABE}=\widehat{AFB}\left(\text{cùng chắn BE}\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABE\sim\Delta AFB\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AE}{AB}\) \(\Rightarrow AB^2=AE.AF\)
5.
\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\)
Pt có 2 nghiệm pb khi \(\left(m-2\right)^2>0\Rightarrow m\ne2\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)
\(\Leftrightarrow m^2-2\left(m-1\right)=m\)
\(\Leftrightarrow m^2-3m+2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=2\left(loại\right)\end{matrix}\right.\)
1.
\(\Delta=9+4m>0\Rightarrow m>-\dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-m\end{matrix}\right.\)
\(5x_1+5x_2=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5\left(x_1+x_2\right)=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5.\left(-3\right)=1-\left(-m\right)^2\)
\(\Leftrightarrow m^2=16\Rightarrow\left[{}\begin{matrix}m=4\\m=-4< -\dfrac{9}{4}\left(loại\right)\end{matrix}\right.\)
2.
\(\Delta=\left(2m+1\right)^2-4\left(m^2+1\right)=4m-3>0\Rightarrow m>\dfrac{3}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+1\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)
\(\Leftrightarrow x_1^2+2x_1+1+x_2^2+2x_2+1=13\)
\(\Leftrightarrow x_1^2+x_2^2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)=11\)
\(\Leftrightarrow2m^2+8m-10=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-5< \dfrac{3}{4}\left(loại\right)\end{matrix}\right.\)