Ai giúp em giải câu 32 với ạ :(
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
21 tháng 9 2021
Xét tính trạng hình dạng cây:
\(\dfrac{Cao}{Thap}=\dfrac{9+3}{3+1}=\dfrac{3}{1}\)
=> Cao THT so với thấp
Quy ước gen: A cao. a thấp
Xét tính trạng màu sắc
\(\dfrac{Đỏ}{vang}=\dfrac{9+3}{3+1}=\dfrac{3}{1}\)
=> đỏ THT so với vàng
Quy ước gen: B đỏ. b vàng
Vì F2 thu dc tỉ lệ 9:3:3:1
=> tuân theo quy luật phân li độc lập Của Menden
=> F1 dị hợp 2 cặp giao tử. kiểu gen F1: AaBb
F1 dị hợp 2 cặp giao tử => P thuần chủng
P Cao,đỏ. x. Thấp,vàng
AABB aabb
Gp AB ab
F1: AaBb( cao,đỏ)
F1 xF1 AaBb( cao,đỏ) x AaBb( cao,đỏ)
GF1 AB,Ab,aB ab AB,Ab,aB,ab
F2: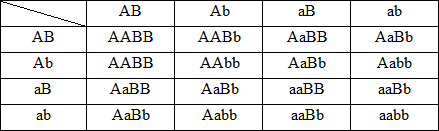
Kiểu gen: 9A_B_:3A_bb:3aaB_:1aabb
kiểu hình:9cao,đỏ :3 cao,vàng:3 thấp,đỏ:1 thấp,vàng
25 tháng 3 2022
Câu 4.
Có \(N_1>N_2\Rightarrow\)Máy hạ thế.
Hiệu điện thế hai đầu cuộn sơ cấp:
\(\dfrac{U_1}{U_2}=\dfrac{N_1}{N_2}\Rightarrow\dfrac{1500}{250}=\dfrac{U_1}{220}\)
\(\Rightarrow U_1=1320V\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
\(A=\left\{1;2;5;10;17\right\}\)
\(\left(x^2-4\right)\left(2x^2-x-1\right)=0\Rightarrow\left[{}\begin{matrix}x^2-4=0\\2x^2-x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm2\\x=1\\x=-\dfrac{1}{2}\notin Z\end{matrix}\right.\) \(\Rightarrow B=\left\{-2;1;2\right\}\)
\(\Rightarrow A\backslash B=\left\{5;10;17\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
I là trung điểm AB \(\Rightarrow\overrightarrow{IB}=\dfrac{1}{2}\overrightarrow{AB}\Rightarrow\overrightarrow{AB}=2\overrightarrow{IB}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
13 tháng 12 2023
Bài 11:
\(PTHH:2A+Cl_2\rightarrow2ACl\\TheoĐLBTKL:\\ m_A+m_{Cl_2}=m_{ACl}\\ \Leftrightarrow 9,2+m_{Cl_2}=23,4\\ \Rightarrow m_{Cl_2}=23,4-9,2=14,2\left(g\right)\\ n_{Cl_2}=\dfrac{14,2}{71}=0,2\left(mol\right)\\ n_A=2.0,2=0,4\left(mol\right)\\ M_A=\dfrac{9,2}{0,4}=23\left(\dfrac{g}{mol}\right)\\ \Rightarrow A\left(I\right):Natri\left(Na=23\right)\)
27 tháng 7 2021
Đặt \(A=\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\)
\(\Leftrightarrow A^3=2+\sqrt{5}+2-\sqrt{5}+3\cdot\sqrt[3]{\left(2+\sqrt{5}\right)\left(2-\sqrt{5}\right)}\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)\)
\(\Leftrightarrow A^3=4+3\cdot\left(-1\right)\cdot A\)
\(\Leftrightarrow A^3=4-3A\)
\(\Leftrightarrow A^3+3A-4=0\)
\(\Leftrightarrow A^3-A^2+A^2-A+4A-4=0\)
\(\Leftrightarrow A^2\left(A-1\right)+A\left(A-1\right)+4\left(A-1\right)=0\)
\(\Leftrightarrow\left(A-1\right)\left(A^2+A+4\right)=0\)
\(\Leftrightarrow A=1\)
Da đây ạ
ABC vuông cân \(\Rightarrow\left\{{}\begin{matrix}AC=AB=3\\BC=AB\sqrt{2}=3\sqrt{2}\end{matrix}\right.\)
\(\overrightarrow{BC}.\overrightarrow{CA}=-\overrightarrow{CB}.\overrightarrow{CA}=-BC.AC.cos\left(\overrightarrow{CB};\overrightarrow{CA}\right)\)
\(=-3\sqrt{2}.3.cos45^0=-9\)