Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi E là trung điểm của BC, F là điểm thuộc cạnh CD sao cho \(\widehat{EAF}=45^0\) và G thuộc cạnh SA. Biết FG //(SBC). Khi đó tỉ số \(\dfrac{GA}{GS}\) là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Phương pháp : Dựng thiết diện.
Cách giải : Gọi I, J lần lượt là giao điểm của GF với AB và AD.
Gọi H là giao điểm của IE và SB.
Gọi K là giao điểm của SD và EJ.
Suy ra thiết diện cần tìm là ngũ giác EHFGK.

Chọn đáp án C
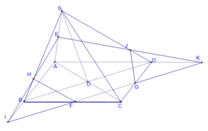
Trong mp (ABCD), gọi

Do đó ngũ giác EHFGJ là thiết diện của hình chóp cắt bởi (EFG)

1: Gọi giao điểm của AC và BD là O trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên (SAC) giao (SBD)=SO
Xét ΔSDC có
P,N lần lượt là trung điểm của DS,DC
=>PN là đường trung bình của ΔSDC
=>PN//SC
PN//SC
SC\(\subset\)(SBC)
PN không nằm trong mp(SBC)
Do đó: PN//(SBC)

Đáp án C
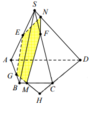
Kẻ EG cắt SB tại I, nối FI cắt BC tại M.
Kẻ GM cắt CD tại H, nối FH cắt SD tại N
Vậy thiết diện cần tìm là ngũ giác GMFNE (hình vẽ bên)
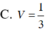
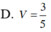
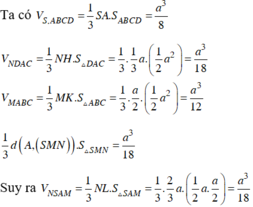
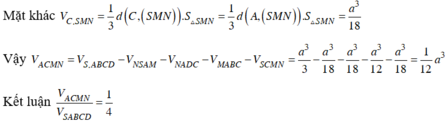
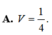
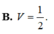
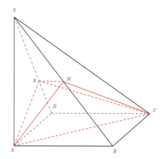

Qua F kẻ đường thẳng song song AD cắt AB tại H
\(\Rightarrow\left(FGH\right)||\left(SBC\right)\Rightarrow GH||\left(SBC\right)\Rightarrow GH||BC\)
Đặt \(\widehat{BAE}=a\) ; \(\widehat{DAF}=b\) (để đỡ dài)
Ta có: \(a+b=90^0-\widehat{EAF}=45^0\)
\(\Rightarrow tan\left(a+b\right)=tan45^0\)
\(\Rightarrow\dfrac{tana+tanb}{1-tana.tanb}=1\)
\(\Rightarrow tana+tanb=1-tana.tanb\)
\(\Rightarrow tanb=\dfrac{1-tana}{1+tana}\)
Mà \(tana=tan\widehat{BAE}=\dfrac{BE}{AB}=\dfrac{1}{2}\)
\(\Rightarrow tanb=tan\widehat{DAF}=\dfrac{DF}{AD}=\dfrac{AH}{AB}=\dfrac{1-\dfrac{1}{2}}{1+\dfrac{1}{2}}=\dfrac{1}{3}\)
\(\Rightarrow3AH=AB=AH+BH\Rightarrow2AH=BH\Rightarrow\dfrac{AH}{BH}=\dfrac{1}{2}\)
Talet: \(\dfrac{GA}{GS}=\dfrac{AH}{BH}=\dfrac{1}{2}\)