cho hình chóp SABCD,đáy là hình bình hành tâm O ,các tam giác SAD và ABC đều cân tại A . Gọi AE,AF là các đường phân giác trong của tam giác ACD và SAB . chứng minh EF//(SAD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
a.
O là trung điểm BD, N là trung điểm CD
\(\Rightarrow\) ON là đường trung bình tam giác BCD
\(\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)\)
Tương tự ta có OM là đtb tam giác SAC \(\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)\)
\(\Rightarrow\left(OMN\right)||\left(SBC\right)\)
b.
Trong mp (SCD), qua E kẻ đường thẳng song song SD cắt SC tại G
\(\Rightarrow EG||SD\Rightarrow EG||\left(SAD\right)\) (1)
Theo định lý Talet: \(\dfrac{EC}{ED}=\dfrac{GC}{GS}\)
Mặt khác AE là phân giác của ACD nên theo định lý phân giác: \(\dfrac{EC}{ED}=\dfrac{AC}{AD}\)
Mà ABC cân tại A \(\Rightarrow AB=AC\); SAD cân tại A \(\Rightarrow AD=SA\)
\(\Rightarrow\dfrac{GC}{GS}=\dfrac{EC}{ED}=\dfrac{AC}{AD}=\dfrac{AB}{SA}\)
AF là phân giác nên áp dụng định lý phân giác:
\(\dfrac{FB}{FS}=\dfrac{AB}{SA}\) \(\Rightarrow\dfrac{FB}{FS}=\dfrac{GC}{GS}\Rightarrow FG||BC\) (Talet đảo)
\(\Rightarrow FG||AD\Rightarrow FG||\left(SAD\right)\) (2)
(1);(2) \(\Rightarrow\left(EFG\right)||\left(SAD\right)\Rightarrow EF||\left(SAD\right)\)
8 tháng 12 2023
Trong mp(SDA), gọi E là giao điểm của SG với AD
Trong mp(SBC), gọi K là giao điểm của SH với BC
Xét ΔSAD có
G là trọng tâm của ΔSAD
E là giao điểm của SG với AD
Do đó: E là trung điểm của AD
Xét ΔSBC có
H là trọng tâm của ΔSBC
SH cắt BC tại K
Do đó: K là trung điểm của BC
Xét hình thang ABCD(AB//CD) có
E,K lần lượt là trung điểm của AD,BC
=>EK là đường trung bình
=>EK//AB
Xét ΔSDE có
SE là đường trung tuyến
G là trọng tâm
Do đó: \(\dfrac{SG}{SE}=\dfrac{2}{3}\)
Xét ΔSBC có
H là trọng tâm của ΔSBC
SK là đường trung tuyến
Do đó: \(\dfrac{SH}{SK}=\dfrac{2}{3}\)
Xét ΔSEK có \(\dfrac{SG}{SE}=\dfrac{SH}{SK}\left(=\dfrac{2}{3}\right)\)
nên GH//EK
mà EK//AB
nên GH//AB
Ta có: GH//AB
AB\(\subset\)(SAB)
GH không nằm trong mp(SAB)
Do đó: GH//(SAB)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
Bạn coi lại đề, sao lại có 2 cái AF là đường cao của 2 tam giác khác nhau thế kia?
CM
22 tháng 4 2018
Đáp án A
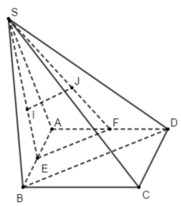
Tam giác SAB có I là trọng tâm và E là trung điểm của AB
Nên ta có S I S E = 2 3 (1)
Tam giác SAD có J là trọng tâm và F là trung điểm của AD
Nên ta có S J S F = 2 3 (2)
Từ (1) và (2) ta có: IJ // EF (3) (định lý Ta-lét trong tam giác SEF)
Tam giác ABD có EF là đường trung bình nên EF // BD (4)
Từ (3) và (4) suy ra IJ // BD
Mà BD (SBD)
Do đó IJ // (SBD).
HT
24 tháng 12 2020
Ta sẽ dựa vô định lý sau: Nếu một đường thẳng song song với một mặt phẳng thì mọi mặt phẳng chứa đường thẳng đó cắt mặt phẳng tại giao tuyến thì giao tuyến đó song song với đường thẳng đã cho
Gọi I là trung điểm SC, K là trung điểm SA
\(MN\subset\left(DKI\right)\)
\(\left(DKI\right)\cap\left(SAC\right)=KI\)
\(Ta-let:\dfrac{DM}{DK}=\dfrac{DN}{DI}=\dfrac{2}{3}\Rightarrow MN//KI\)
\(\Rightarrow MN//\left(SAC\right)\)
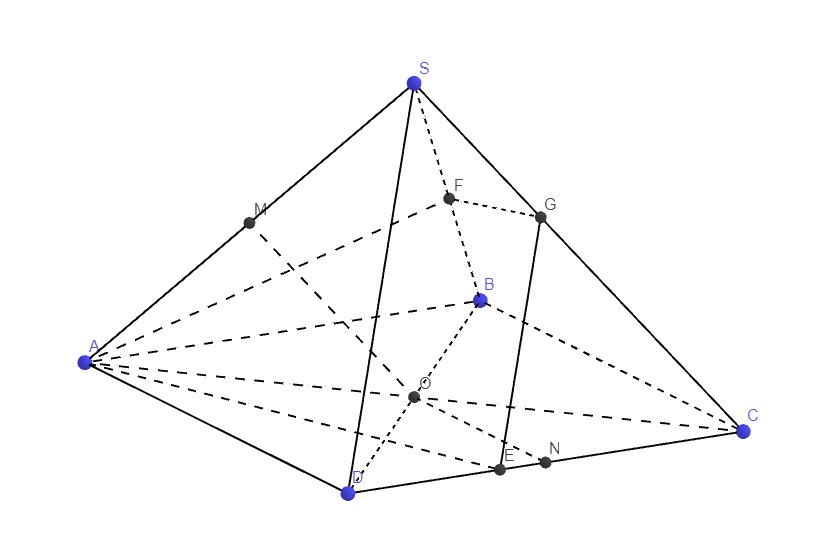
Qua E kẻ đường thẳng song song SD cắt SC tại G \(\Rightarrow\dfrac{GC}{GS}=\dfrac{EC}{ED}\) (Talet)
Mặt khác theo định lý phân giác: \(\dfrac{EC}{ED}=\dfrac{AC}{AD}\Rightarrow\dfrac{GC}{GS}=\dfrac{AC}{AD}=\dfrac{AB}{SA}\) (do AC=AB và AD=SA)
Theo định lý phân giác: \(\dfrac{AB}{SA}=\dfrac{FB}{FS}\Rightarrow\dfrac{GC}{GS}=\dfrac{FB}{FS}\Rightarrow FG||BC\Rightarrow FG||AD\)
\(\Rightarrow\left(EFG\right)||\left(SAD\right)\Rightarrow EF||SAD\)