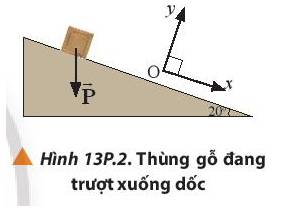
Một chiếc thùng gỗ khối lượng m đang trượt xuống từ một dốc nghiêng 200 so với phương ngang như Hình 13P.2. Em hãy phân tích thành phần vectơ trọng lực tác dụng lên thùng gỗ theo các phương Ox và Oy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
QT
Quoc Tran Anh Le
Giáo viên
12 tháng 12 2023
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
3 tháng 11 2023
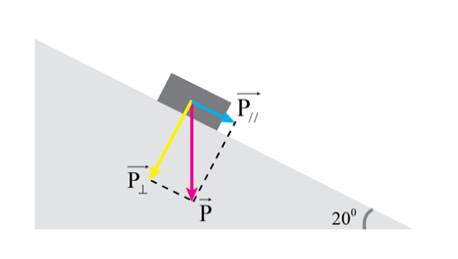
a)
Giản đồ vectơ các lực tác dụng lên thùng hàng:
b)
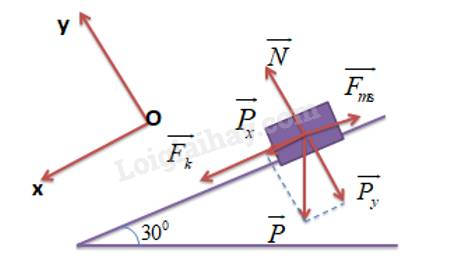
Ta có:
\({P_x} = P.\sin \alpha = 500.\sin {30^0} = 250N\)
\({P_y} = P.\cos \alpha = 500.\cos {30^0} = 500.\frac{{\sqrt 3 }}{2} = 250\sqrt 3 N\)
c)
Lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc vì nó cân bằng với thành phần \(\overrightarrow {{P_y}} \) của trọng lực.
d)
Chiếu các lực tác dụng lên trục Ox ta được:
\({F_k} - {F_{ms}} = ma \Leftrightarrow {F_k} - \mu N = ma\) (1)
Chiếu các lực tác dụng lên trục Oy ta được:
\(N - P.\cos \alpha = 0 \Leftrightarrow N = P.\cos \alpha = 250\sqrt 3 N\) (2)
Thay vào (1) ta được:
\(250 - \mu .250\sqrt 3 = \frac{{500}}{{10}}.2,00\)
\( \Leftrightarrow \mu = \frac{{150}}{{250\sqrt 3 }} = \frac{{\sqrt 3 }}{5} \approx 0,346\)
Vậy hệ số ma sát trượt giữa mặt dốc và thùng hàng là 0,346.
VT
9 tháng 4 2018
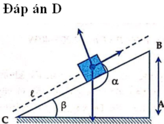
Công của trọng lực thực hiện từ lúc vật lên dốc đến lúc dừng lại trên dốc bằng: Ap=mgh
Với h là hiệu độ cao từ vị trí đầu đến vị trí cuối, tính theo hình ta có:
12 tháng 10 2023
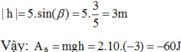
a)Lực tác dụng vào thùng gỗ theo phương ngang:
\(F=m\cdot a+\mu mg=5\cdot0,22+0,2\cdot5\cdot10=11,1N\)
b)Khi \(F_k=10N\) thì lực ma sát lúc này:
\(F_{ms}=F_k-m\cdot a=10-5\cdot0,22=8,9N\)
c)Lực tác dụng vào thùng gỗ với \(a=0,4m/s^2\) là:
\(F'=m\cdot a+\mu mg=5\cdot0,4+0,2\cdot5\cdot10=12N\)
d)Với vận tốc \(v=3m/s\) đến khi ngừng kéo thì gia tốc mới của vật là:
\(m\cdot a=-\mu mg\Rightarrow a=-\mu g=-0,2\cdot10=-2m/s^2\)
Quãng đường tối đa thùng trượt được:
\(v^2-v_0^2=2aS\Rightarrow S=\dfrac{v^2-v_0^2}{2a}=\dfrac{-3^2}{2\cdot\left(-2\right)}=2,25m\)