Giải hộ mình 3 bài vs ạ ! Mình đg cần gấp để nộp !

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét ΔABC vuông tại A và ΔFEC vuông tại F có
\(\widehat{ECF}\) chung
Do đó: ΔABC\(\sim\)ΔFEC(g-g)
Suy ra: \(\dfrac{CA}{CF}=\dfrac{CB}{CE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(CA\cdot CE=CB\cdot CF\)(Đpcm)
b) Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)


a: góc DAC=90-40=50 độ
b: góc ADB=90 độ
c: góc DAB=90-80=10 độ
=>góc BAE=10+50=60 độ
góc AED=180-60=120 độ

3 năm trước tuổi cha gấp 10 lần tuổi con=>cha 10 phần,con 1 phần.Hiệu số phần = nhau là:10-1=9 phần
3 năm sau gấp 4 lần tuổi con=>vậy tuổi cha có số phần là:9x4=36 phần
thời gian từ 3 năm trước đến 3 năm sau là:3+3=6 năm
hiệu số phần =nhau của tuổi cha là:36-9=27 phần
Giá trị của 1 phần là:27:9=3 tuổi
tuổi cha 3 năm trước là:3x10=30 tuổi
Tuổi cha bây giờ là:30+3=33 tuổi

Bài 3:
Xét ΔBAC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: DE là đường trung bình của ΔBAC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)
Hình thang EDCB có
M là trung điểm của EB
N là trung điểm của DC
Do đó: MN là đường trung bình của hình thang EDCB
Suy ra: MN//ED//BC và \(MN=\dfrac{ED+BC}{2}\)
\(\Leftrightarrow MN=\left(\dfrac{1}{2}BC+BC\right):2=\dfrac{3}{4}BC\)
Xét ΔEBD có
M là trung điểm của EB
MI//ED
Do đó: I là trung điểm của BD
Xét ΔBED có
M là trung điểm của EB
I là trung điểm của BD
Do đó: MI là đường trung bình của ΔBED
Suy ra: \(MI=\dfrac{ED}{2}=\dfrac{1}{4}BC\left(1\right)\)
Xét ΔECD có
N là trung điểm của DC
NK//ED
Do đó: K là trung điểm của EC
Xét ΔECD có
N là trung điểm của DC
K là trung điểm của EC
Do đó: NK là đường trung bình của ΔECD
Suy ra: \(NK=\dfrac{ED}{2}=\dfrac{1}{4}BC\left(2\right)\)
Ta có: MI+IK+KN=MN
nên \(IK=\dfrac{1}{4}BC\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra MI=IK=KN

May yêu dấu,
Tớ đã được nghe dì Hồng kể về cậu rất nhiều. Bởi vậy mà hôm nay, tớ viết bức thư này với mong muốn được làm quen với cậu. Đặc biệt, tớ muốn kể cho cậu nghe về nơi quê hương của tớ.
Đầu thư, tớ sẽ giới thiệu về bản thân mình. Tớ là Minh Anh. Năm nay tám tuổi, bằng tuổi cậu. Hiện tại, tớ đang là học sinh lớp 3A, trường tiểu học (tên trường). Môn học yêu thích nhất là môn Tiếng Anh. Những lúc rảnh rỗi, tớ thường đọc sách, xem hoạt hình. Tớ cũng rất thích tìm hiểu về các nước trên thế giới. Trong bức thư tới, cậu hãy kể cho tớ nghe về nước Mĩ nhé.
Còn bây giờ, tớ sẽ giới thiệu cho cậu về đất nước của tớ. Việt Nam là một nước nằm ở châu Á. Lịch sử của đất nước tớ đã trải qua hàng nghìn năm. Không chỉ vậy, đất nước của tớ có truyền thống văn hóa lâu đời. Thiên nhiên Việt Nam phân hóa rất đa dạng. Còn con người Việt Nam rất thân thiện, hiếu khách.
Thành phố mà tớ đang sống là Hà Nội - thủ đô của Việt Nam. Hà Nội là một thành phố rất rộng lớn. Đường phố rộng rãi, hiện đại và lúc nào cũng tấp nập xe cộ đi lại. Hai bên đường nhiều tòa nhà cao tầng mọc san sát nhau. Các hàng quán luôn đông đúc. Không chỉ vậy, Hà Nội còn có rất nhiều điểm du lịch nổi tiếng như Hồ Hoàn Kiếm, Lăng Bác, Chùa Một Cột, Công viên thủ lệ... Nhưng em đặc biệt thích nhất là Hồ Hoàn Kiếm (hay còn gọi là Hồ Gươm). Đây là nơi đã gắn với sự tích về vua Lê Lợi trả gươm thần cho Rùa Vàng. Xung quanh hồ còn có cầu Thê Húc và đền Ngọc Sơn. Cầu Thê Húc được sơn màu đỏ, cong cong như con tôm. Qua cầu Thê Húc là đến đền Ngọc Sơn cổ kính, uy nghiêm. Hà Nội vừa mang vẻ đẹp hiện đại, vừa mang vẻ đẹp cổ kính.
Dĩ nhiên, một thành phố không thể làm nên vẻ đẹp của cả một đất nước. Nhưng Hà Nội đã mang những vẻ đẹp tiêu biểu nhất của Việt Nam. Tớ cũng tự hào khi được sinh sống ở thủ đô xinh đẹp này.
Dì Hồng kể rằng cậu là một cô gái rất dễ thương. Cậu còn thích đọc sách giống tớ. Và đặc biệt là May rất yêu thích đất nước Việt Nam phải không? Nếu như cậu có dịp đến thăm Việt Nam, tớ sẽ đưa cậu đi tham quan đất nước của tớ.
Cuối thư, tớ chúc cậu học tập thật tốt. Mong sớm nhận được hồi âm từ cậu.
Bạn của cậu
Khánh Ngọc

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-20\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=8-3a=8-3\cdot7=-13\end{matrix}\right.\)



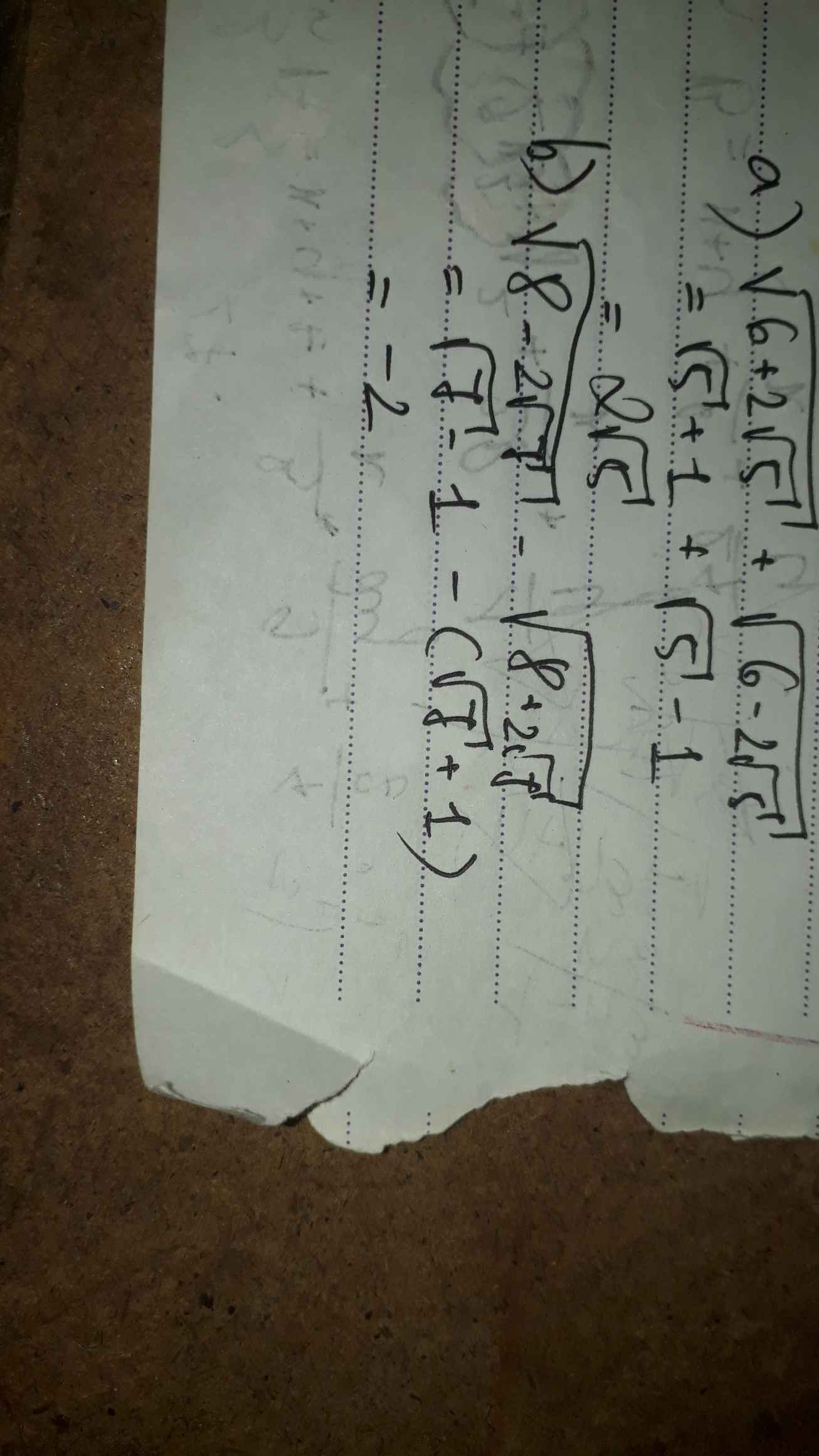


 giải hộ mình vs ạ mình cần gấp ạ
giải hộ mình vs ạ mình cần gấp ạ


16)
a) Tam giác ABC vuông tại A : \(AB^2+AC^2=BC^2\)
BC=10 ⇒FC=10-5.2=4.8
b) Tam giác ABC và tam giác FEC có
C chung
\(\dfrac{AC}{FC}=\dfrac{BC}{EC}=0.6\)
Do đó tam giác ABC đồng dạng với tam giác FEC (C-G-C)
c)⇒Góc FEC=ABC=AEM
Tam giác MAE và tam giác MFB có
Góc M chung
Góc AEM = MBF (CMT)
⇒ 2 Tam giác đồng dạng (G-G)
⇒\(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)⇒ MA.MB=MF.MB
a) Xét \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\) (Định lí Py-ta-go)
=> \(BC^2=6^2+8^2=100\)
=> BC = 10 (cm)
=> CF = BC\(-\)BF = 10 - 5,2 = 4,8 (cm)
Vậy BC = 10 cm ; CF = 4,8 cm
b) Xét \(\Delta CAB\) và \(\Delta CFE\) có
\(\left\{{}\begin{matrix}\widehat{C}:chung\\\dfrac{CF}{CE}=\dfrac{CA}{CB}\left(\dfrac{4,8}{6}=\dfrac{8}{10}=\dfrac{4}{5}\right)\end{matrix}\right.\)
=>\(\Delta CAB\sim\Delta CFE\) (c-g-c)
Vậy \(\Delta CAB\sim\Delta CFE\)
c) Xét \(\Delta MAEvà\Delta MFB\) có
\(\left\{{}\begin{matrix}\widehat{M}:chung\\\widehat{MAE}=\widehat{MFB}=90^0\end{matrix}\right.\)
=> \(\Delta MAE\sim\Delta MFB\) (g-g)
=> \(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)
=> MA.MB = MF.ME
Vậy MA.MB = ME.MF
d) Xét \(\Delta BMF\) và \(\Delta BCA\) có
\(\left\{{}\begin{matrix}\widehat{B}:chung\\\widehat{BFM}=\widehat{BAC}=90^0\end{matrix}\right.\)
=> \(\Delta BMF\) \(\sim\)\(\Delta BCA\) (g-g)
=> \(\dfrac{MF}{AC}=\dfrac{BF}{BA}\)
=> MF = \(\dfrac{8.5,2}{6}\) = \(\dfrac{104}{15}\approx6,9\left(cm\right)\)
Vậy MF \(\approx6,9\left(cm\right)\)