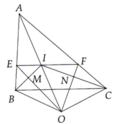
Bài 4 (2.5 điểm) Cho tam giác $A B C$ có $A D$ là phân giác của $\widehat{B A C}$. Từ $D$ kẻ các đường thẳng song song với $A B$ và $A C$ lần lượt cắt $A C, \, A B$ tại $E, \, F$
a) Chứng minh tứ giác $A E D F$ là hình thoi.
b) Trên tia đối của tia $F A$ lấy điểm $G$ sao cho $F A=F G$. Chứng minh $E F G D$ là hình bình hành.
c) Lấy điểm $I$ sao cho $F$ là trung điểm $ID$. Tia $IA$ cắt tia $D E$ tại $K$. Gọi $O$ là giao điểm của $A D$ và $E F$. Chứng minh $\mathrm{O}$ là trung điểm của $GK$.