 mới học đl Tha les chx học đồng dạng nên làn thalez thôi ạ chi tiết
mới học đl Tha les chx học đồng dạng nên làn thalez thôi ạ chi tiết
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(3x-3=3\left(x-1\right)\)
\(4-4x=-4\left(x-1\right)\)
\(x^2-1=\left(x-1\right)\left(x+1\right)\)
\(\Rightarrow\) MTC là \(3.\left(-4\right).\left(x-1\right)\left(x+1\right)=-12\left(x-1\right)\left(x+1\right)\)
Do đó:
\(\dfrac{11x}{3x-3}=\dfrac{11x}{3\left(x-1\right)}=\dfrac{11x.\left(-4\right).\left(x+1\right)}{3\left(x-1\right).\left(-4\right)\left(x+1\right)}=\dfrac{-44x\left(x+1\right)}{-12\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{5}{4-4x}=\dfrac{5}{-4\left(x-1\right)}=\dfrac{5.3\left(x+1\right)}{-4\left(x-1\right).3\left(x+1\right)}=\dfrac{15\left(x+1\right)}{-12\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{2x}{x^2-1}=\dfrac{2x}{\left(x-1\right)\left(x+1\right)}=\dfrac{2x.\left(-12\right)}{-12\left(x-1\right)\left(x+1\right)}=\dfrac{-24x}{-12\left(x-1\right)\left(x+1\right)}\)

5:
a: \(-120x^5y^4=20x^5y^2\cdot\left(-6y^2\right)\)
b: \(60x^6y^2=20x^5y^2\cdot3x\)
c: \(-5x^{15}y^3=20x^5y^2\cdot\left(-\dfrac{1}{4}x^{10}y\right)\)
d: \(2x^{12}y^{10}=20x^5y^2\cdot\left(\dfrac{1}{10}x^7y^8\right)\)

11)
\(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{x^{2^{ }}-4}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{x^2-2^2}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{\left(x-2\right)\left(x+2\right)}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{x\left(x-3\right)}{2}\)

Gọi thời gian vòi I chảy riêng đến khi đầy bể là \(x\) (giờ)
Trong 1 giờ vòi I chảy được \(\dfrac{1}{x}\) bể.
Đổi: 1 giờ 20 phút = \(\dfrac{4}{3}\) giờ
Mỗi giờ hai vòi chảy được là \(\dfrac{1}{\dfrac{4}{3}}=\dfrac{3}{4}\) bể, vậy mỗi giờ vòi II chảy được \(\dfrac{3}{4}-\dfrac{1}{x}\) (bể)
Đổi: 10 phút = \(\dfrac{1}{6}\) (giờ), 12 phút = \(\dfrac{1}{5}\) (giờ)
Ta có phương trình: \(\dfrac{1}{6}.\dfrac{1}{x}+\dfrac{1}{5}.\left(\dfrac{3}{4}-\dfrac{1}{x}\right)=\dfrac{2}{15}\)
\(\Rightarrow\dfrac{1}{6x}+\dfrac{3}{20}-\dfrac{1}{5x}=\dfrac{2}{15}\Rightarrow-\dfrac{1}{30x}=-\dfrac{1}{60}\Rightarrow x=2\)
Vậy vòi I chảy riêng trong 2 giờ sẽ đầy bể.
Mỗi giờ vòi II chảy được là \(\dfrac{3}{4}-\dfrac{1}{2}=\dfrac{1}{4}\) bể, nên vòi II chảy riêng trong 4 giờ thì đầy bể.

Lời giải:
\(\frac{2x-2\sqrt{x}+2}{x-\sqrt{x}}=\frac{2(x-\sqrt{x})+2}{x-\sqrt{x}}=\frac{2(x-\sqrt{x})+2}{x-\sqrt{x}}=2+\frac{2}{x-\sqrt{x}}\)
\(\dfrac{2x-2\sqrt{x}+2}{x\sqrt{x}+1}=\dfrac{2}{\sqrt{x}+1}\)

\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)

a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: \(HD=\sqrt{10^2-8^2}=6\left(cm\right)\)
\(S_{ADHE}=6\cdot8=48\left(cm^2\right)\)
c: Để ADHE là hình vuông thì AH là phân giác của góc BAC
=>góc B=45 độ

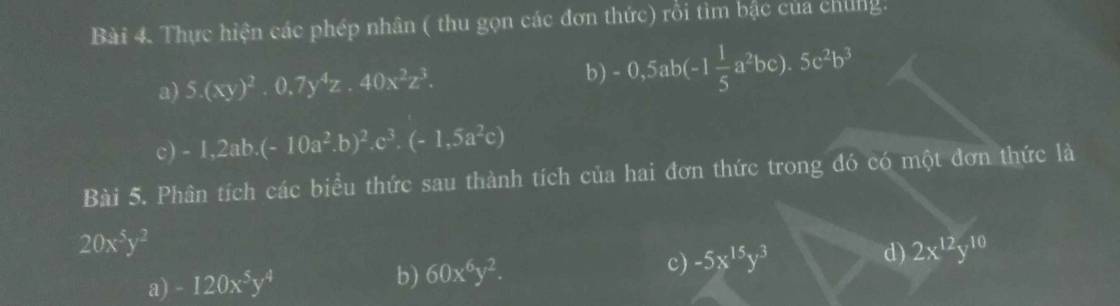






a: AB//CD
=>\(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(KA\cdot KD=KB\cdot KC\)
b:
Chx hiểu câu b ạ tại sao dòng thứ 2 phải đảo lôn lên ạ