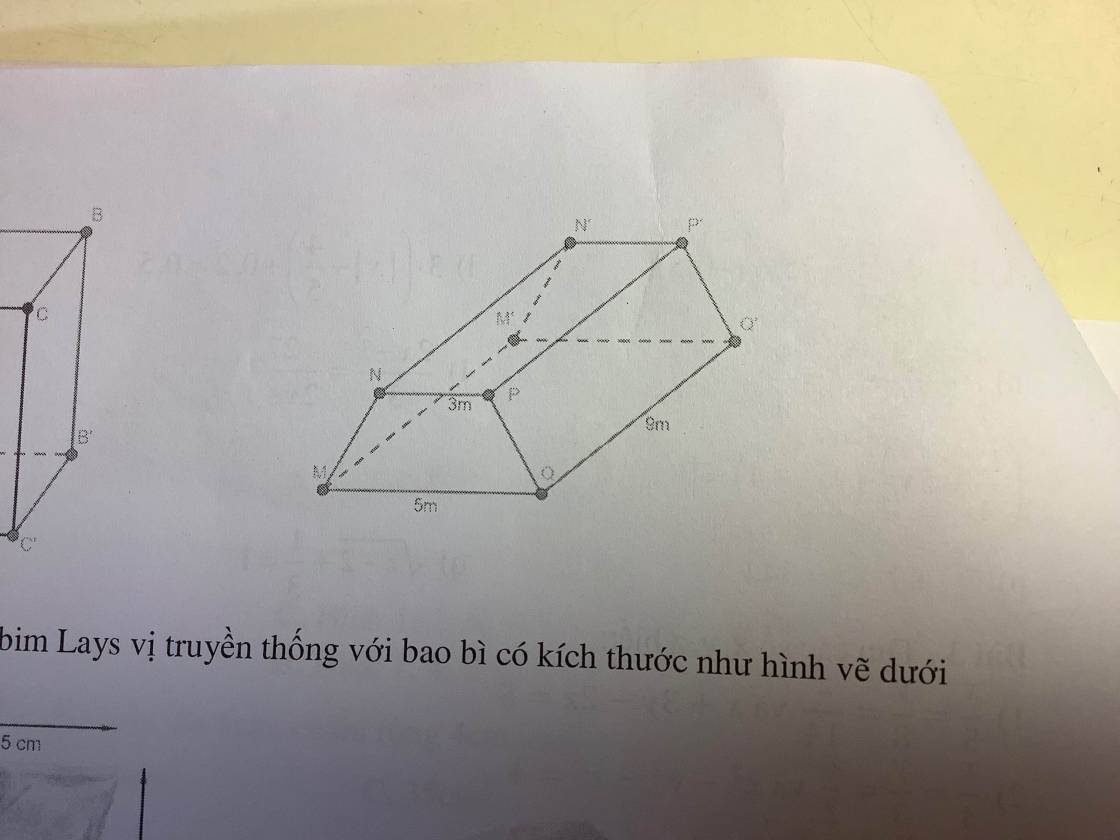
Tính diện tích xung quanh và thể tích hình lăng trụ đứng tam giác MNPQ.M'N'P'Q'. Biết đáy MNPQ là hình thang cân có độ dài 2 cạnh MQ=5m, NP=3m và chiều cao hình thang là 2,83m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
i) Hình 33b là hình lăng trụ đứng tam giác
Hình 33a là hình lăng trụ đứng tứ giác
ii) Hình 33a: Sxq = (3+4+5+8).5 = 100 (cm2)
Hình 33b: Sxq = (3+4+5).6 = 72 (cm2)
iii) Hình 33a: Diện tích đáy là: (8+4).3:2=18 (cm2)
Thể tích là: V = 18.5 = 90 (cm3)
Hình 33b: Diện tích đáy là: \(\dfrac{1}{2}3.4=6\) (cm2)
Thể tích là: V= 6.6=36 (cm3)
5 tháng 5 2019
a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
5 tháng 5 2019
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2
26 tháng 12 2023
Chu vi đáy là 3+4+5=12(cm)
Diện tích xung quanh của hình trụ là:
\(S_{xq}=12\cdot7=84\left(cm^2\right)\)
Vì \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
Thể tích của lăng trụ là:
\(V=S_{đáy}\cdot cao=6\cdot7=42\left(cm^3\right)\)
CM
21 tháng 2 2018
Xét tam giác ABC có nửa chu vi của tam giác là:
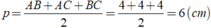
Khi đó ta có
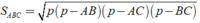
+ Diện tích xung quanh của hình lăng trụ
30 tháng 4 2023
Áp dụng định lí Py - Ta - Go , độ dài cạnh còn lại của mặt đáy tam giác là :
\(\sqrt{3^2+4^2}=5\left(cm\right)\)
Diện tích xung quanh hình lăng trụ đứng :
\(S_{xq}=\left(3+4+5\right).8=96\left(cm^2\right)\)
Diện tích toàn phần :
\(S_{tp}=96+\left(3.4\right)=108\left(cm^2\right)\)
Thể tích :
\(V=\dfrac{3.4}{2}.8=48\left(cm^3\right)\)
MH
26 tháng 4 2022
Bình phương cạnh huyền của đáy là: \(6^2+8^2=100\)
\(\Rightarrow\) Cạnh huyền của đáy là \(10\left(cm\right)\)
Diện tích xung quanh lăng trụ là: \(\left(6+8+10\right).3=72\left(cm^2\right)\)
Diện tích đáy lăng trụ là: \(\dfrac{1}{2}.6.8=24\left(cm^2\right)\)
Thể tích lăng trụ là: \(24.3=72\left(cm^3\right)\)